|
| 1 | +## Explanation |
| 2 | + |
| 3 | +### Strategy |
| 4 | + |
| 5 | +**Restate the problem** |
| 6 | + |
| 7 | +We are given a binary matrix and need to create a difference matrix where each cell `diff[i][j]` is calculated as: ones in row i + ones in column j - zeros in row i - zeros in column j. |
| 8 | + |
| 9 | +**1.1 Constraints & Complexity** |
| 10 | + |
| 11 | +- **Input Size:** The matrix can have up to 10^5 rows and columns, with total cells up to 10^5. |
| 12 | +- **Time Complexity:** O(m*n) - We need to traverse the matrix twice: once to count ones in rows and columns, and once to build the result matrix. |
| 13 | +- **Space Complexity:** O(m + n) - We store arrays for row and column counts. |
| 14 | +- **Edge Case:** Empty matrix or single cell matrix are handled naturally by the algorithm. |
| 15 | + |
| 16 | +**1.2 High-level approach** |
| 17 | + |
| 18 | +The goal is to compute the difference matrix efficiently by precomputing row and column statistics. Instead of recalculating counts for each cell, we count ones in each row and column once, then use these counts to compute each cell's value. |
| 19 | + |
| 20 | +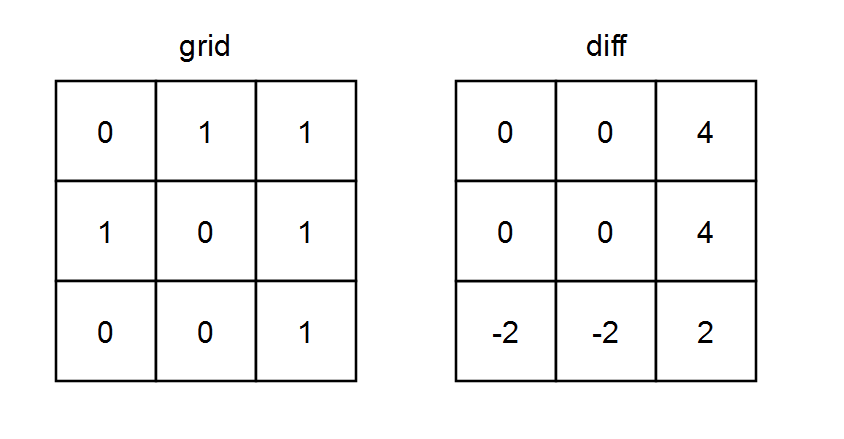 |
| 21 | + |
| 22 | +**1.3 Brute force vs. optimized strategy** |
| 23 | + |
| 24 | +- **Brute Force:** For each cell (i, j), count ones and zeros in row i and column j separately. This results in O(m*n*(m+n)) time complexity, which is inefficient. |
| 25 | +- **Optimized Strategy:** Precompute ones count for all rows and columns in O(m*n) time, then compute each cell in O(1) time using the precomputed values. Total time is O(m*n). |
| 26 | +- **Why optimized is better:** We avoid redundant calculations by reusing row and column statistics across all cells in the same row or column. |
| 27 | + |
| 28 | +**1.4 Decomposition** |
| 29 | + |
| 30 | +1. **Count Row Statistics:** Traverse the matrix once to count the number of ones in each row. |
| 31 | +2. **Count Column Statistics:** During the same traversal, count the number of ones in each column. |
| 32 | +3. **Calculate Zeros:** For each row, zeros = total columns - ones. For each column, zeros = total rows - ones. |
| 33 | +4. **Build Result Matrix:** For each cell (i, j), compute diff[i][j] = ones_row[i] + ones_col[j] - zeros_row[i] - zeros_col[j]. |
| 34 | + |
| 35 | +### Steps |
| 36 | + |
| 37 | +**2.1 Initialization & Example Setup** |
| 38 | + |
| 39 | +Let's use the example: `grid = [[0,1,1],[1,0,1],[0,0,1]]` |
| 40 | + |
| 41 | +- Matrix dimensions: 3 rows × 3 columns |
| 42 | +- Initialize `ones_row = [0, 0, 0]` and `ones_col = [0, 0, 0]` |
| 43 | + |
| 44 | +**2.2 Start Counting** |
| 45 | + |
| 46 | +Traverse the matrix to count ones: |
| 47 | +- Row 0: [0,1,1] → ones_row[0] = 2 |
| 48 | +- Row 1: [1,0,1] → ones_row[1] = 2 |
| 49 | +- Row 2: [0,0,1] → ones_row[2] = 1 |
| 50 | + |
| 51 | +- Column 0: [0,1,0] → ones_col[0] = 1 |
| 52 | +- Column 1: [1,0,0] → ones_col[1] = 1 |
| 53 | +- Column 2: [1,1,1] → ones_col[2] = 3 |
| 54 | + |
| 55 | +**2.3 Trace Walkthrough** |
| 56 | + |
| 57 | +| Cell (i,j) | ones_row[i] | ones_col[j] | zeros_row[i] | zeros_col[j] | diff[i][j] | |
| 58 | +|------------|-------------|-------------|--------------|--------------|------------| |
| 59 | +| (0,0) | 2 | 1 | 1 | 2 | 2+1-1-2 = 0 | |
| 60 | +| (0,1) | 2 | 1 | 1 | 2 | 2+1-1-2 = 0 | |
| 61 | +| (0,2) | 2 | 3 | 1 | 0 | 2+3-1-0 = 4 | |
| 62 | +| (1,0) | 2 | 1 | 1 | 2 | 2+1-1-2 = 0 | |
| 63 | +| (1,1) | 2 | 1 | 1 | 2 | 2+1-1-2 = 0 | |
| 64 | +| (1,2) | 2 | 3 | 1 | 0 | 2+3-1-0 = 4 | |
| 65 | +| (2,0) | 1 | 1 | 2 | 2 | 1+1-2-2 = -2 | |
| 66 | +| (2,1) | 1 | 1 | 2 | 2 | 1+1-2-2 = -2 | |
| 67 | +| (2,2) | 1 | 3 | 2 | 0 | 1+3-2-0 = 2 | |
| 68 | + |
| 69 | +**2.4 Build Result** |
| 70 | + |
| 71 | +Create result matrix `res` with dimensions 3×3 and fill each cell using the formula. |
| 72 | + |
| 73 | +**2.5 Return Result** |
| 74 | + |
| 75 | +Return `[[0,0,4],[0,0,4],[-2,-2,2]]`, which matches the expected output. |
0 commit comments