|
| 1 | +## Explanation |
| 2 | + |
| 3 | +### Strategy |
| 4 | + |
| 5 | +**Restate the problem** |
| 6 | + |
| 7 | +We need to divide a long corridor (a string of 'S' for seats and 'P' for plants) into non-overlapping sections. Each section must contain exactly two seats and can have any number of plants. Room dividers can be installed between positions in the corridor. We need to count the number of different ways to place these dividers to create valid sections. |
| 8 | + |
| 9 | +**1.1 Constraints & Complexity** |
| 10 | + |
| 11 | +- **Input Size:** The corridor length `n` can be up to 10^5 characters. |
| 12 | +- **Time Complexity:** O(n) - We traverse the corridor once to count seats and process segments. |
| 13 | +- **Space Complexity:** O(1) - We only use a few variables to track state, no additional data structures proportional to input size. |
| 14 | +- **Edge Case:** If the total number of seats is odd or zero, there's no valid way to divide the corridor (each section needs exactly 2 seats). |
| 15 | + |
| 16 | +**1.2 High-level approach** |
| 17 | + |
| 18 | +The goal is to partition the corridor into segments where each segment contains exactly two seats. Between any two adjacent segments, we must place exactly one divider. The key insight is that if there are `k` plants between two segments, we can place the divider in `k + 1` different positions (before each plant and after the last plant). The total number of ways is the product of all these possibilities. |
| 19 | + |
| 20 | +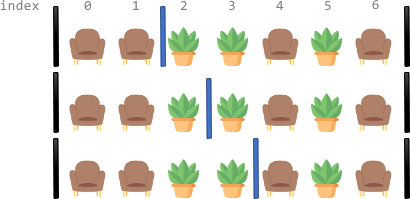 |
| 21 | + |
| 22 | +**1.3 Brute force vs. optimized strategy** |
| 23 | + |
| 24 | +- **Brute Force:** Try all possible positions to place dividers and check if each configuration creates valid segments. This would require checking 2^(n-1) possible configurations, resulting in O(2^n) time complexity, which is exponential and inefficient. |
| 25 | +- **Optimized Strategy:** Process the corridor linearly, identify segments (pairs of seats), and count plants between segments. Multiply the number of divider positions between each pair of segments. This runs in O(n) time with O(1) space. |
| 26 | +- **Why optimized is better:** We avoid exponential enumeration by recognizing that the problem decomposes into independent choices between segments, allowing us to compute the answer as a product of possibilities. |
| 27 | + |
| 28 | +**1.4 Decomposition** |
| 29 | + |
| 30 | +1. **Validate Input:** Count total seats. If the count is odd or zero, return 0 immediately (no valid division possible). |
| 31 | +2. **Process Segments:** Traverse the corridor, grouping seats into pairs. Each pair forms one segment. |
| 32 | +3. **Count Divider Positions:** Between each pair of adjacent segments, count the number of plants. The number of ways to place a divider is (number of plants + 1). |
| 33 | +4. **Calculate Result:** Multiply all the divider placement possibilities together, taking modulo 10^9 + 7 to handle large numbers. |
| 34 | + |
| 35 | +### Steps |
| 36 | + |
| 37 | +**2.1 Initialization & Example Setup** |
| 38 | + |
| 39 | +Let's use the example: `corridor = "SSPPSPS"` |
| 40 | + |
| 41 | +- Total seats: 4 (even, so valid) |
| 42 | +- Segments: We need to create 2 segments (4 seats ÷ 2 = 2 segments) |
| 43 | +- First segment: "SS" (positions 0-1) |
| 44 | +- Plants between: "PP" (positions 2-3) |
| 45 | +- Second segment: "SPS" (positions 4-6, but we only need 2 seats: positions 4 and 6) |
| 46 | + |
| 47 | +**2.2 Start Processing** |
| 48 | + |
| 49 | +Initialize: |
| 50 | +- `res = 1` (we'll multiply possibilities) |
| 51 | +- `seats_seen = 0` (track seats in current segment) |
| 52 | +- `i = 0` (current position) |
| 53 | + |
| 54 | +**2.3 Trace Walkthrough** |
| 55 | + |
| 56 | +| Position (i) | Character | Seats Seen | Action | Result (res) | |
| 57 | +|--------------|-----------|------------|--------|---------------| |
| 58 | +| 0 | 'S' | 1 | Found first seat | 1 | |
| 59 | +| 1 | 'S' | 2 | Found second seat, segment complete | 1 | |
| 60 | +| 2-3 | 'P', 'P' | 2 | Count plants between segments: 2 plants | 1 | |
| 61 | +| 4 | 'S' | 1 (reset) | Found first seat of next segment | 1 × (2+1) = 3 | |
| 62 | +| 5 | 'P' | 1 | Plant in segment | 3 | |
| 63 | +| 6 | 'S' | 2 | Found second seat, segment complete | 3 | |
| 64 | + |
| 65 | +**2.4 Increment and Loop** |
| 66 | + |
| 67 | +After completing a segment (finding 2 seats): |
| 68 | +- Count plants until the next seat is found |
| 69 | +- Multiply `res` by (plants_between + 1) |
| 70 | +- Reset `seats_seen` to 0 for the next segment |
| 71 | +- Continue processing from the position after the plants |
| 72 | + |
| 73 | +**2.5 Return Result** |
| 74 | + |
| 75 | +For `corridor = "SSPPSPS"`: |
| 76 | +- First segment ends at position 1 |
| 77 | +- Between segments: 2 plants (positions 2-3) |
| 78 | +- Divider positions: 2 + 1 = 3 ways |
| 79 | +- Final result: `res = 3` |
| 80 | + |
| 81 | +The function returns `3`, which matches the expected output. |
0 commit comments