diff --git a/First_Date_with_TensorFlow.ipynb b/First_Date_with_TensorFlow.ipynb
new file mode 100644
index 0000000..55ef6d4
--- /dev/null
+++ b/First_Date_with_TensorFlow.ipynb
@@ -0,0 +1,1002 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "8199f0e0-9eb0-44d5-ea02-358ec66c4676"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 204
+ },
+ "outputId": "0c918045-df97-451f-bad0-985448c5c3d1"
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 4,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "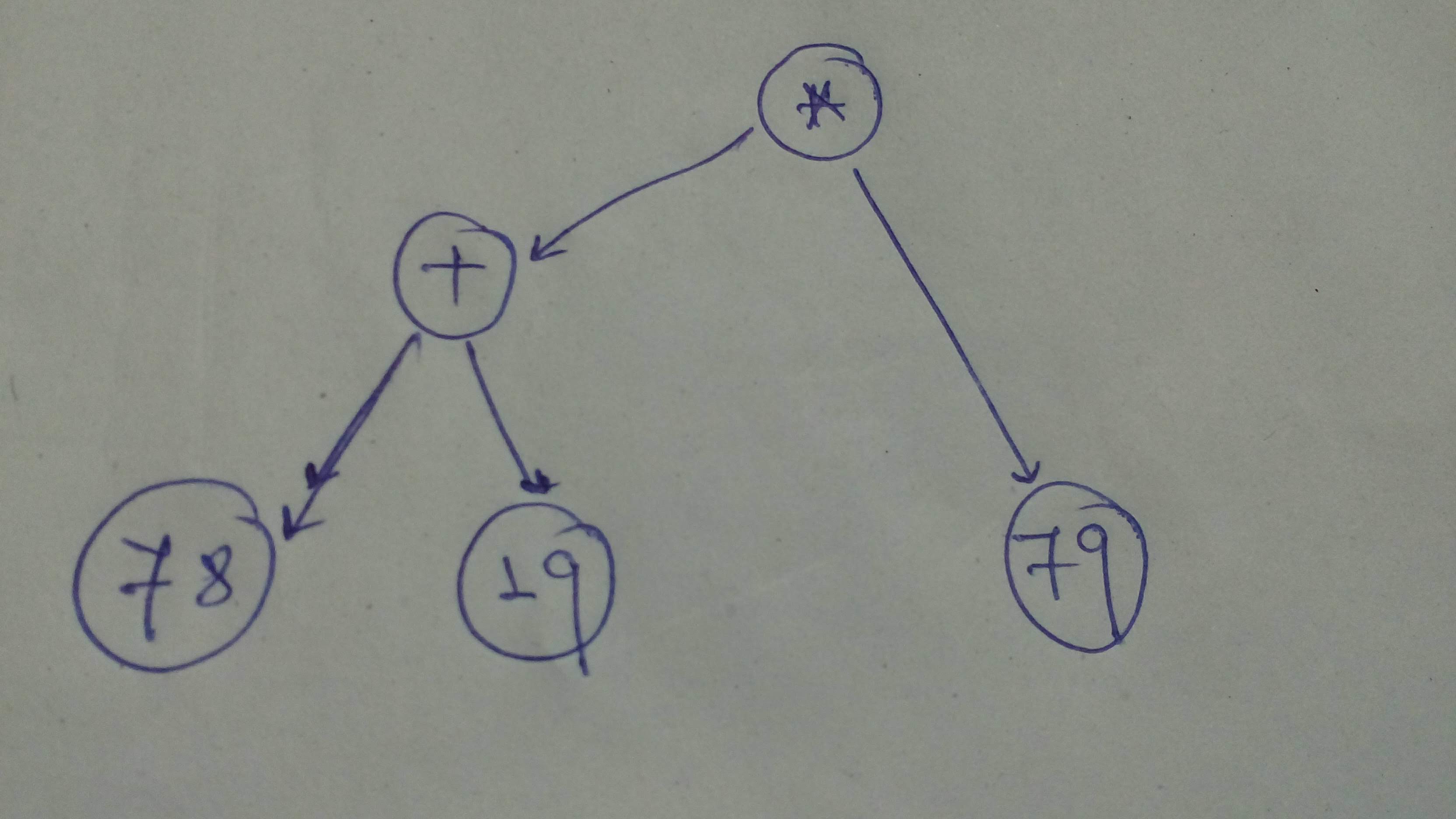"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 51
+ },
+ "outputId": "fa907c8c-2af9-4843-f651-214c879e5e53"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "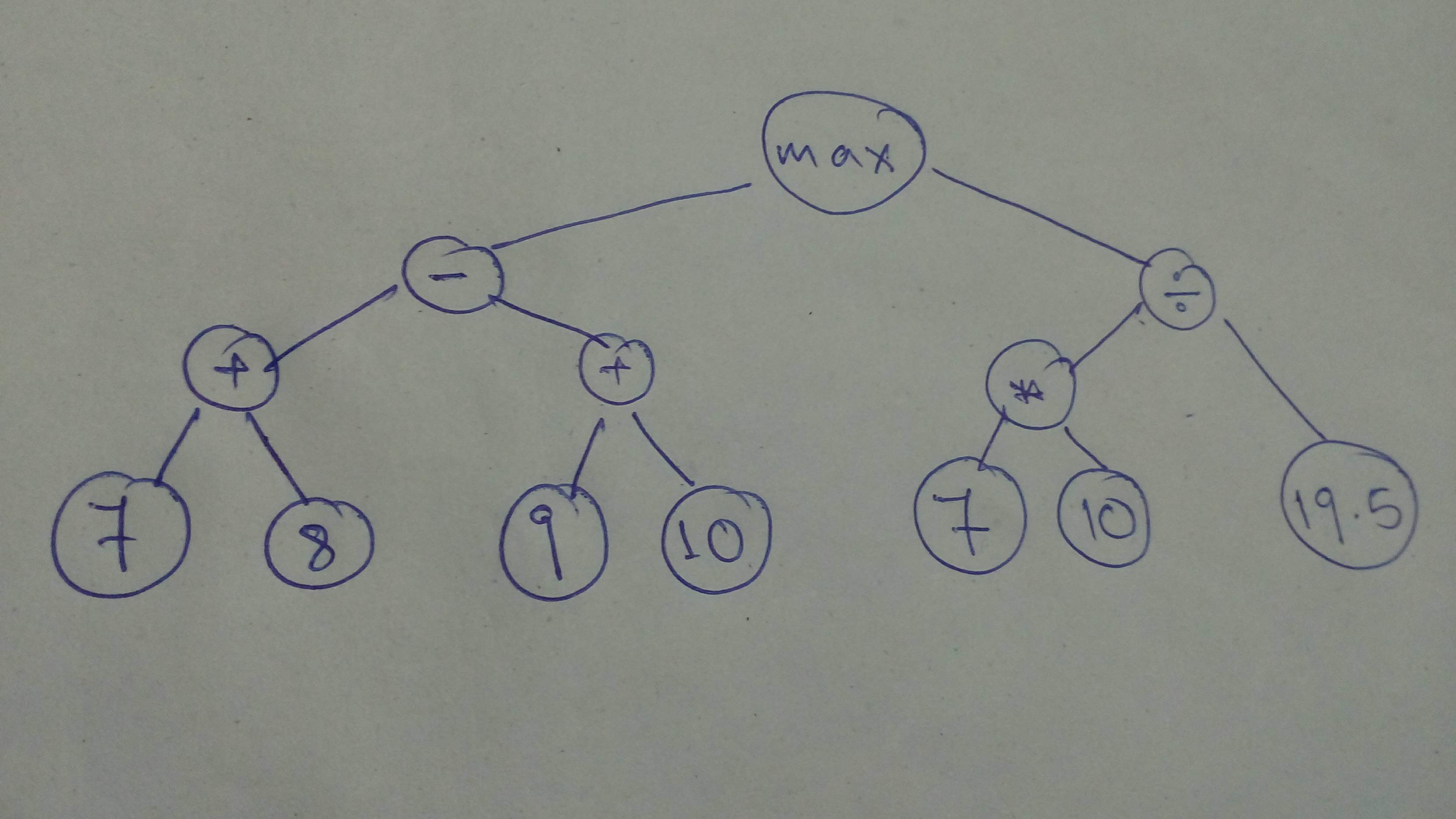"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "25887724-a56f-4c05-dda6-4d766cf6e6bd"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "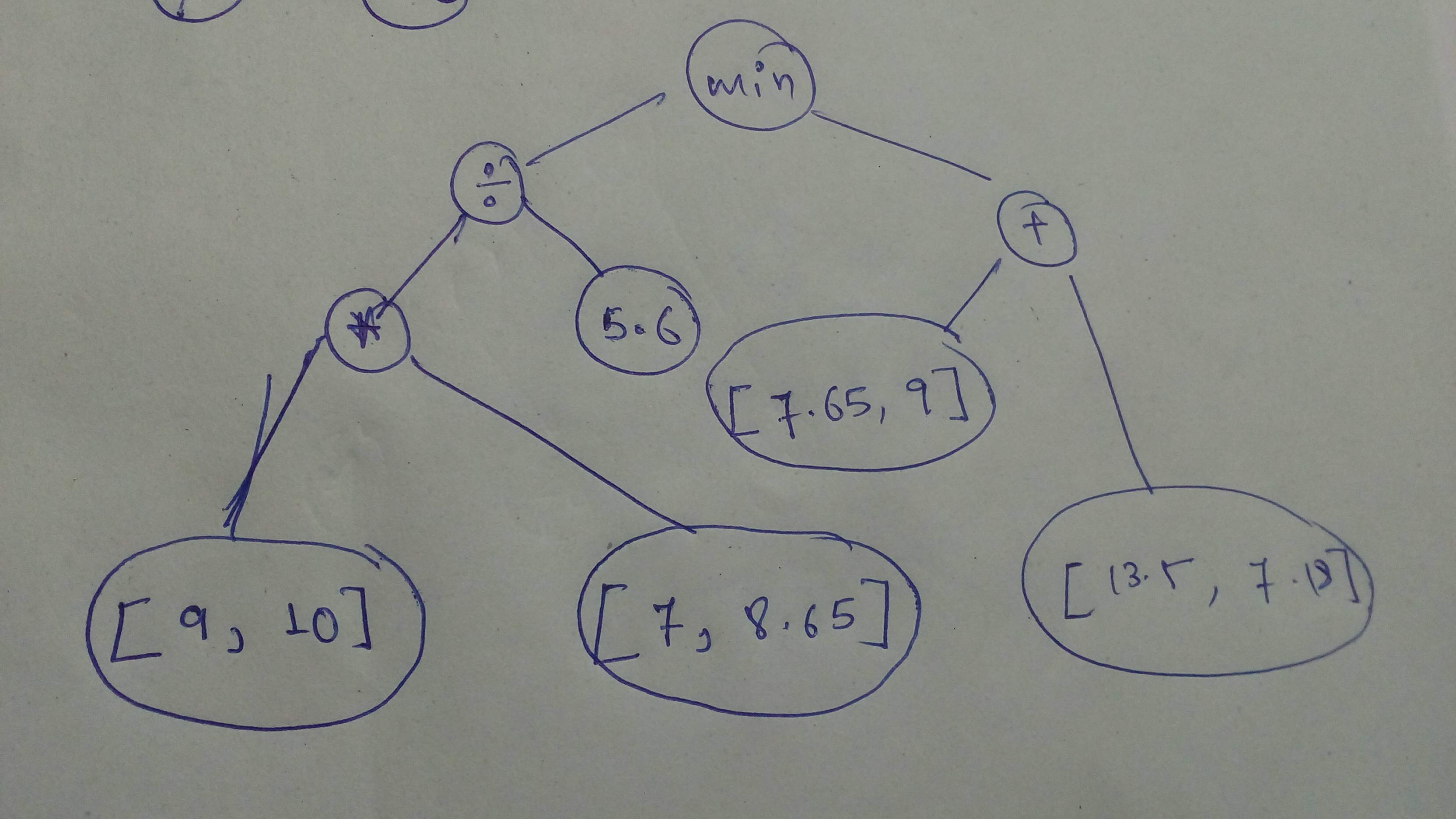\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "ec1f00bc-1508-4f72-8f8b-e591435c7295"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "n1=tf.constant([9, 10],dtype=tf.float32)\n",
+ "n2=tf.constant([7, 8.65],dtype=tf.float32)\n",
+ "graph1=tf.divide(tf.cast(tf.multiply(n1,n2),dtype=tf.float32),tf.constant(5.6))\n",
+ "n3 = tf.constant([7.65,9],dtype=tf.float32)\n",
+ "n4 = tf.constant([13.5,7.18],dtype=tf.float32)\n",
+ "graph2=tf.add(n3,n4)\n",
+ "final_graph=tf.minimum(graph1,graph2)\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess = tf.Session()\n",
+ "left_graph, right_graph, final_result = sess.run([graph1, graph2, final_graph])\n",
+ "print ('Left Graph : ', (left_graph))\n",
+ "print ('Right Graph : ', (right_graph))\n",
+ "print ('Final Result : ', (final_result))\n",
+ "sess.close()"
+ ],
+ "execution_count": 11,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Left Graph : [11.25 15.446429]\n",
+ "Right Graph : [21.15 16.18]\n",
+ "Final Result : [11.25 15.446429]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "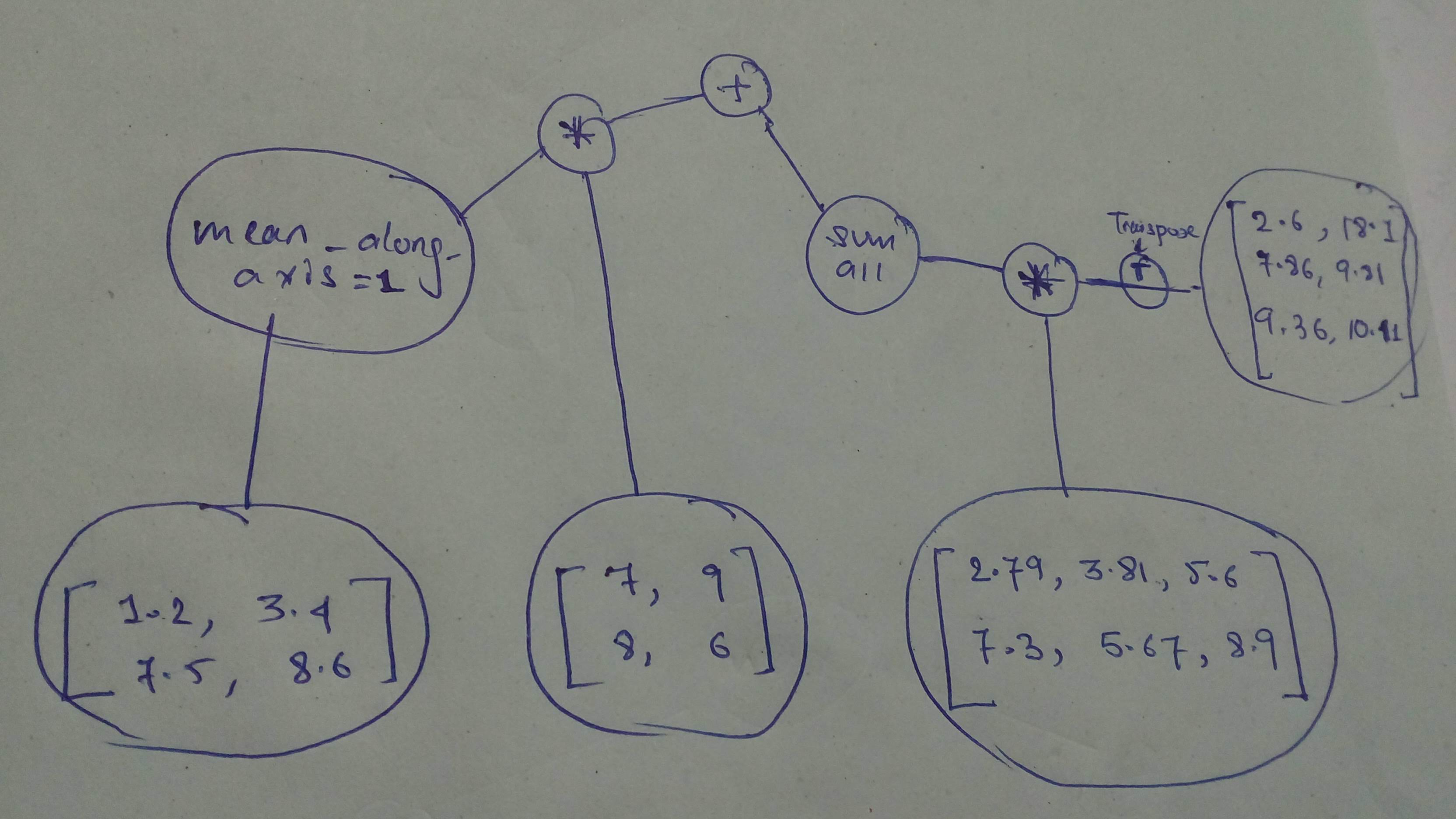"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 153
+ },
+ "outputId": "8d589dcd-3a12-44c4-d56d-2f27cf830eac"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "m1 = tf.constant([[1.2, 3.4], [7.5, 8.6]], dtype = tf.float32)\n",
+ "m2 = tf.constant([[7.0, 9.0], [8.0, 6.0]], dtype = tf.float32)\n",
+ "m3 = tf.constant([[2.79, 3.81, 5.6], [7.3, 5.67, 8.9]], dtype = tf.float32)\n",
+ "m4 = tf.constant([[2.6, 18.1], [7.86, 9.81], [9.36,10.11]], dtype = tf.float32)\n",
+ "graph1=tf.multiply(tf.cast(tf.reduce_mean(m1,1), dtype = tf.float32), m2)\n",
+ "graph2 =tf.reduce_sum(tf.multiply(tf.cast(tf.matrix_transpose(m4), dtype = tf.float32 ), m3))\n",
+ "final_graph = tf.math.add(graph1,graph2)\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess = tf.Session()\n",
+ "left_graph, right_graph, final_result = sess.run([graph1, graph2, final_graph])\n",
+ "print ('Left Graph:\\n', (left_graph))\n",
+ "print ('Right Graph:\\n', (right_graph))\n",
+ "print ('Result:\\n', (final_result))\n",
+ "sess.close()"
+ ],
+ "execution_count": 10,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Left Graph:\n",
+ " [[16.100002 72.450005]\n",
+ " [18.400002 48.300003]]\n",
+ "Right Graph:\n",
+ " 367.3483\n",
+ "Result:\n",
+ " [[383.4483 439.7983 ]\n",
+ " [385.7483 415.64832]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ "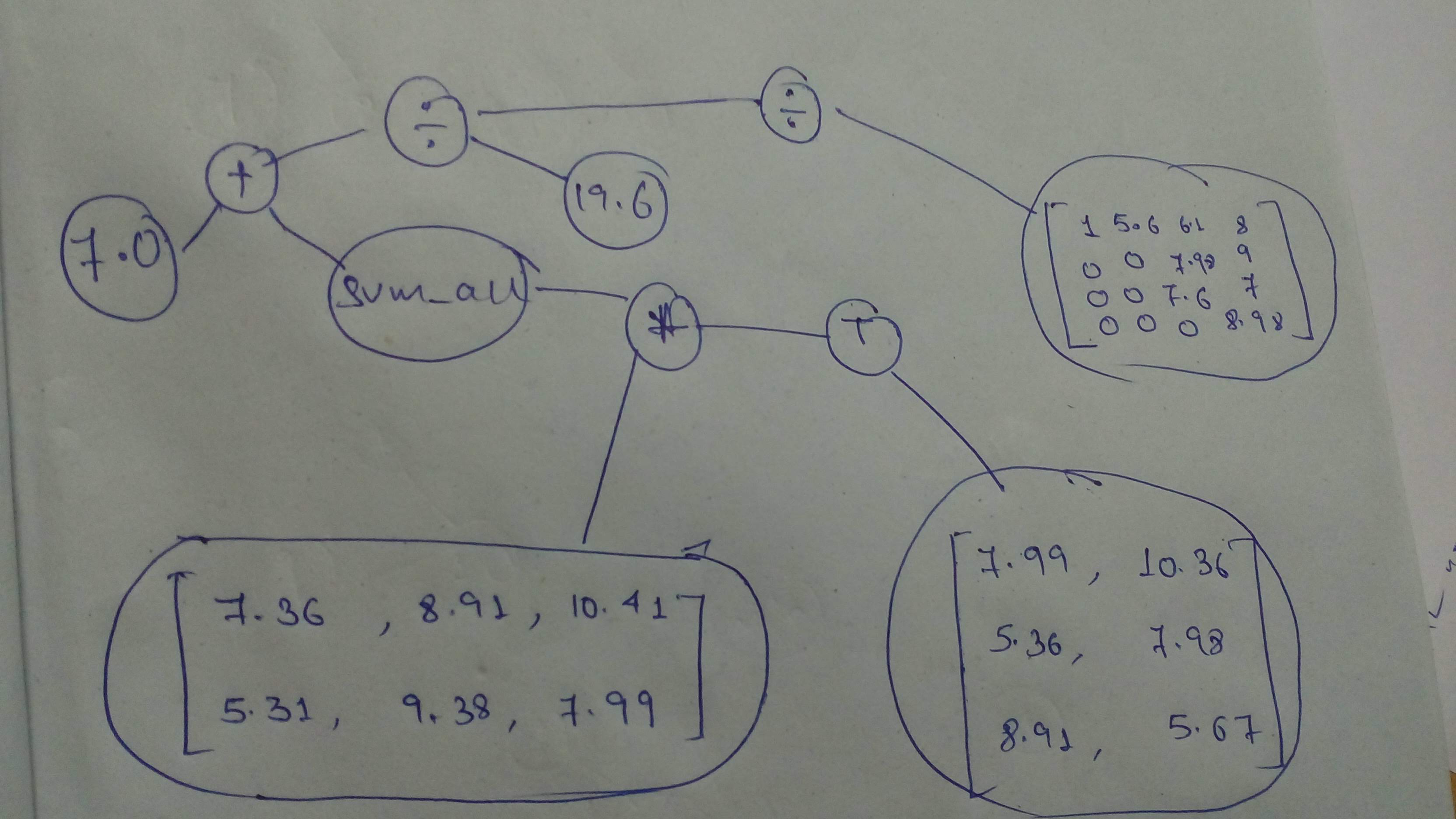"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 85
+ },
+ "outputId": "161796cc-6436-4f0d-f874-18608dfb67cc"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "m1 = tf.constant([[7.36, 8.91, 10.41], [5.31, 9.38, 7.99]] , dtype = tf.float32)\n",
+ "m2 = tf.constant([[7.99, 10.36], [5.36, 7.98], [8.91, 5.67]] , dtype = tf.float32)\n",
+ "m3 = tf.constant([[1.0, 5.6, 6.1, 8.0], [0, 0, 7.98, 9.0], [0, 0, 7.6, 7], [0, 0, 0, 8.98]] , dtype = tf.float32)\n",
+ "final_graph=tf.divide(tf.divide(tf.add(tf.reduce_sum(m1 * tf.transpose(m2)), tf.constant(7.0)),tf.constant(19.6)),m3)\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess=tf.Session()\n",
+ "result=sess.run(final_graph)\n",
+ "print(result)\n",
+ "sess.close()"
+ ],
+ "execution_count": 14,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[19.463488 3.475623 3.1907358 2.432936 ]\n",
+ " [ inf inf 2.4390335 2.1626098]\n",
+ " [ inf inf 2.5609853 2.7804983]\n",
+ " [ inf inf inf 2.1674263]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "outputId": "810dd01a-8592-40ea-e983-05dd43142bc8",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 17,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFKCAYAAADmCN3IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3XtcFXX+x/HX4Q4KCgaY1/KeKV7w\nUhCWJppmZSkWbZbFVl5SW92SsLxsumqFGWm5pqW1phtaZqZ4C20N8kaRabaa4Y1EUBABldv8/qj4\nLWuKHoHhnPN+Ph77x5kzM+fzYdzeZ+Y7Z74WwzAMRERExCY5mV2AiIiIWE9BLiIiYsMU5CIiIjZM\nQS4iImLDFOQiIiI2TEEuIiJiw1ys2aioqIjo6GjS09NxdnZmxowZNG7cuNw6q1evZsmSJTg5OTFk\nyBAiIiLIyMggJiaGwsJCSktLeeGFF2jXrh29evWifv36ODs7A/Daa68RGBh4yc/PzDxrTdmX5evr\nRXZ2QaXvtyZTz47BEXsGx+xbPds3f3/vP1xuVZCvWbMGHx8fYmNj2bZtG7GxscyZM6fs/YKCAubN\nm8eKFStwdXVl8ODBhIeHs3jxYsLDw3nooYdISUnh9ddfZ9GiRQC888471KpVy5pyKoWLi7Npn20W\n9ewYHLFncMy+1bNjsurSenJyMuHh4QCEhISQkpJS7v3U1FTat2+Pt7c3Hh4edO7cmZSUFHx9fcnJ\nyQEgNzcXX1/fayxfRETEsVl1Rp6VlYWfnx8ATk5OWCwWCgsLcXNzu+h9AD8/PzIzMxk2bBiDBw9m\n1apV5OXlsWzZsrJ1Jk+ezPHjxwkODmb8+PFYLJZLfr6vr1eVfAu71GULe6aeHYMj9gyO2bd6djwV\nBnl8fDzx8fHllqWmppZ7XdFTXn9/f+HChfTr148RI0aQmJjIrFmzmDt3LmPGjCEsLIw6deowatQo\n1q9fz1133XXJ/VXFeIi/v3eVjL3XZOrZMThiz+CYfatn+3apLywVXlqPiIjgo48+Kve/+++/n8zM\nTODXG98Mwyg7GwcICAggKyur7PXJkycJCAggJSWFsLAwAEJDQ/n+++8BGDhwIPXq1cPFxYUePXrw\nn//8x/pORUREHIhVY+ShoaEkJCQAkJiYSPfu3cu936FDB/bs2UNubi75+fmkpKTQpUsXmjZtWnY2\n/91339G0aVPOnj1LVFQUhYWFAOzcuZOWLVteS08iIiIOw6ox8v79+5OUlERkZCRubm7MnDkTgAUL\nFtC1a1c6derE+PHjiYqKwmKxMGrUKLy9vXn66aeZOHFi2ZeAiRMn4u3tTY8ePXjwwQdxd3enbdu2\nl72sLiIiIv/PYovTmFbFeIgjjbP8Tj07BkfsGRyzb/Vs36weIxcREZGaS0EuIiJiwxTkIiIiNkxB\nLiIiNVZGQQZL9r7Lf07/WOEzSxyVVXeti4iIVLXi0mIeX/cndmXsAKCpzw30aXoXfW7ox60NQnFz\ndqtgD45BQS4iIjXSvG/eYFfGDsIa3UFd97okHtnMO3vm886e+dR29eaOxr0Y3P5+uvqG4e/lb3a5\nplGQi4hIjfN91h5e2fl3Ar3qs7DPYnw9/CgsKeTrX5LYkLaO9WnrWHPoU9Yc+hQLFjoHdik7W29b\n7+bLztdhb/Q78t840m8Rf6eeHYMj9gyO2be99Hyh5AJ94u/gh9N7WT5gJb2ahF+0jmEYHMw5QFJW\nIh/vXcWOX76mxCgBoGHtRoQ37UvfG/oR2rAHHi4e1d1ClajU+chFRESqyis7/s4Pp/fyaNsn/jDE\nASwWCy19WxHSKpjHWj5N9vnTJB7dzIa0dWw+sonFexexeO8ivFy86NHoDvrc0I/wpn0JrFW/mrup\negpyERGpMb7+JZm538yhqc8NTAmddsXb+Xr48UDLCB5oGUFxaTE7T2xnfdo6NqYlkJC2loS0tQB0\n8O9Enxvuok/Tu2jv3wEni+3/eEuX1n9jL5ekroZ6dgyO2DM4Zt+23nNeUR49/xXCkdzDrL5/Pd2v\nv6XCba6k50NnfmJT2nrWH04gOX0bxaXFAAR61afPDXcR3vQuwhrdTi3XWpXSR1XRpXUREanRpnz1\nIodz0xjd6S9XFOJXqlmd5jzVYSRPdRhJ7oUzbD2WyPq0dWw+vIEP9i3mg32LcXd257aGPcouwTfy\nblxpn1/VFOQiImK6zYc38P6+d7nJ72ae7xZTZZ/j416He5oP5J7mAykpLSHl5C42pq3/NdiPbGTz\nkY1MANrWa0ff387WOwUE4+zkXGU1XStdWv+NrV+SsoZ6dgyO2DM4Zt+22vPp86e4ffmtnD5/ivWD\nt9DuuvZXvG1l9nz07BE2pCWw8XAC2459SWFpIQDXeV5H76Z9CW96F3c07om3m0+lfN7V0qV1ERGp\nkaK/HE9GwQlevGXKVYV4ZWvs3YSo9k8R1f4p8ory+PLoFjYeTmDj4fUs37+U5fuX4urkSkiD28rG\n1m+oc6Np9f5OQS4iIqb55MAKVh38mK71uzOq41izyylT27U2/ZsNoH+zAZQapXyX+e2vd8EfXs/W\nY4lsPZbIxG0TaO3bhvDf7oLvUr8bLk7VH6u6tP4bW70kdS3Us2NwxJ7BMfu2tZ5P5P9Cj+XdKSwp\n5IsHv6JZneZXvQ8zev4lL52Nh9ez8XACXx7bwrnicwD4uvvSq0k4fW64i15NelPHvW6lfq4urYuI\nSI1hGAbPJo4i50IOr/R43aoQN8v1tRvw6M2P8+jNj3Ou+BxfHf+S9WkJbExLYOWBj1h54CO8XLzY\nFPFvWvi2rPJ6FOQiIlLt3t/3Hl8c2UTPxnfy2M1PmF2O1TxdPOndtC+9m/bF6DGbvae+Z0PaOg7m\nHMDP069aalCQi4hItTp05icmfxVDHfe6zOk5z24mOLFYLLS7rn2137CnIBcRkWpTUlrC6M3DKSgu\nYH7PN7m+dgOzS7J5tv+QWRERsRnzvo1j54nt3Nf8Ae5vMdjscuyCglxERKrF3qzvmbVjGgFegcy6\nPdZuLqmbTUEuIiJV7kLJBUZtfoqi0iLm9JyLn0c9s0uyGwpyERGpcq/umMG+U98ztO3j9G7a1+xy\n7IqCXEREqtSOX7Yz99tf5xifGjrd7HLsjoJcRESqTF5RHs9sfgrDMHjzzn9Q27W22SXZHQW5iIhU\nmb8lvURa7s+M7DiGW66/1exy7JKCXEREqsQXRzaxeO8ibvJry4RuE80ux24pyEVEpNJlnz/Ns4mj\ncHVyZW7vBXi4eJhdkt1SkIuISKV74d9/5UT+LzzX9QXaXxdkdjl2TUEuIiKVatWBlXx8YAXBgV15\nptOzZpdj9xTkIiJSaU7k/8KEL8fh5eLFvDv/gYuTpvSoalb9hYuKioiOjiY9PR1nZ2dmzJhB48aN\ny62zevVqlixZgpOTE0OGDCEiIoKCggKio6PJysrC09OTmTNn4u/vz/79+5kyZQoArVu3ZurUqdfc\nmIiIVC/DMPhL4jNkX8hmZo9YmtVtYXZJDsGqM/I1a9bg4+PDsmXLGD58OLGxseXeLygoYN68eSxe\nvJgPPviAJUuWkJOTw0cffUTjxo358MMPGTFiBHFxcQBMnz6dmJgYli9fTl5eHlu3br32zkREpFp9\nsG8xm49s5PZGPXn85j+bXY7DsCrIk5OTCQ8PByAkJISUlJRy76emptK+fXu8vb3x8PCgc+fOpKSk\nkJaWRlDQrzc9dOnShd27d1NYWMjx48fLlvfs2ZPk5ORr6UlERKpZ2pmfmfTbHONv9HpLE6JUI6su\nrWdlZeHn5weAk5MTFouFwsJC3NzcLnofwM/Pj8zMTFq1asXWrVvp27cvO3bsID09nezsbHx8fMrW\nrVevHpmZmZf9fF9fL1xcnK0p/bL8/b0rfZ81nXp2DI7YMzhm32b0XFJawgNrRlFQnM/Se5fS4cY2\n1fr5jnic/1uFQR4fH098fHy5ZampqeVeG4Zx2X38/v7gwYP58ccfiYyMpFu3buXC/kr3BZCdXVDh\nOlfL39+bzMyzlb7fmkw9OwZH7Bkcs2+zep77zRtsO7KNe5oPpHfggGqtwZGO86W+sFQY5BEREURE\nRJRbFh0dTWZmJm3atKGoqAjDMMrOxgECAgLIysoqe33y5Ek6duyIm5tb2Y1s+fn5bN68GT8/P3Jy\ncsrWzcjIICAg4Oq6ExERU+w7tZeZ21/G3zOAV3q8rkvqJrBqjDw0NJSEhAQAEhMT6d69e7n3O3To\nwJ49e8jNzSU/P5+UlBS6dOnC1q1bmTNnDvDrXe1hYWG4urrSrFkzdu3aBcCGDRsICwu7lp5ERKQa\nFJYUMmrTUxSWFvJ6zzep56k5xs1g1Rh5//79SUpKIjIyEjc3N2bOnAnAggUL6Nq1K506dWL8+PFE\nRUVhsVgYNWoU3t7edO/enaVLlzJkyBDq1KnD7NmzAYiJiWHSpEmUlpbSoUMHQkJCKq9DERGpEq/t\nnMneU3t45KbH6HNDP7PLcVgW40oGpWuYqhgPcaRxlt+pZ8fgiD2DY/ZdnT3vPLGdez7pS6Pajdny\nYBK13cy54cyRjvOlxsj1ZDcREbkq+UX5PLP56d/mGJ9vWojLrxTkIiJyVf6W/BI/nznEiI6jubVB\nqNnlODwFuYiIXLHEI5t57/uFtPG7iehuL5pdjqAgFxGRK5RzPptnE0fh4uTCvDs1x3hNoSAXEZEr\n8sK/n+OX/HT+2iWa9v4dzC5HfqMgFxGRCq0++AkrD3xE54BgxnQeZ3Y58l8U5CIiclkZ+Sd4/su/\n4Oniydw7F2iO8RpGR0NERC7JMAzGbRnN6fOnmRH2Ki18W5pdkvwPnZGLiMglLf3hfTYeXk+PRj15\nvN2TZpcjf0BBLiIifyjtzM+89NUL+LjV4Y2e83CyKDJqIl1aFxGRi5SUljDmixHkF+Ux784FNPRu\nZHZJcgn6eiUiIheZnzqPr39JYkCz+xjc6kGzy5HLUJCLiEg5P5zax4ztf/t1jvHbNcd4TacgFxGR\nMoUlhTyz+WkKSwuZ3fNNrvO8zuySpAIKchERKTN71yz2ZKXycJuh9NUc4zZBQS4iIgDsOrGDOSmx\nNPZuwsu3zTC7HLlCCnIREaGgqOD/5xjvNR9vNx+zS5IrpCAXERFe/noSh878xNMdRhHS8Dazy5Gr\noCAXEXFwW45+waI9C2jt24aY7pPMLkeukoJcRMSB5ZzPZuwXI3FxcmHunf/QHOM2SEEuIuLAYrY9\nzy/56YzvMoEOAZ3MLkesoCAXEXFQn/30KSv+8y86BwQztvN4s8sRKynIRUQcUEZBBs9tHYuHs4fm\nGLdxOnIiIg7GMAz+umUMp8+fZvptszTHuI3TGbmIiINZtv+frE9bR1jD24lq/7TZ5cg1UpCLiDiQ\nw7lpTNw2AW83H97o9ZbmGLcDurQuIuIgSo3SsjnG3+w1n0bejc0uSSqBglxExAEUlxbzcvJkktO/\nov+N9zCkdaTZJUklUZCLiNi59LzjjNj0Z5LTv6KJzw28dscbmmPcjmhwRETEjm1IW0evj0JJTv+K\nAc3uY3PEl5pj3M7ojFxExA4VlhTy8teT+UfqPNyd3ZnVYzbDbo7SmbgdUpCLiNiZn88c4ukNj/Nt\n5je0qNuSBX0W0+669maXJVXEqiAvKioiOjqa9PR0nJ2dmTFjBo0bl7/7cfXq1SxZsgQnJyeGDBlC\nREQEBQUFREdHk5WVhaenJzNnzsTf35+hQ4dSUFCAl5cXABMmTKBdu3bX3p2IiIP55MAKxm8ZS17R\nWR5q8ydmhL1GLddaZpclVciqIF+zZg0+Pj7Exsaybds2YmNjmTNnTtn7BQUFzJs3jxUrVuDq6srg\nwYMJDw9n1apVNG7cmLi4OHbt2kVcXBwvv/wyADNmzKBVq1aV05WIiIMpKCrgydXjWPjNQrxcajHv\nzgVEtH7I7LKkGlh1s1tycjLh4eEAhISEkJKSUu791NRU2rdvj7e3Nx4eHnTu3JmUlBTS0tIICgoC\noEuXLuzevfsayxcRkR9O7aPvijtY+M1C2l/Xgc1DvlSIOxCrzsizsrLw8/MDwMnJCYvFQmFhIW5u\nbhe9D+Dn50dmZiatWrVi69at9O3blx07dpCenl62TlxcHNnZ2TRv3pyYmBg8PC49J66vrxcuLs7W\nlH5Z/v7elb7Pmk49OwZH7Bnsv2/DMFiYspAxCWM4X3ye0d1G82r4q7i7uJtdWrWy9+NckQqDPD4+\nnvj4+HLLUlNTy702DOOy+/j9/cGDB/Pjjz8SGRlJt27dysL+0UcfpXXr1jRp0oTJkyezdOlSoqKi\nLrm/7OyCisq+av7+3mRmnq30/dZk6tkxOGLPYP995144w1+3jmXVwY+p616X+b3f5bHukb/1XGh2\nedXG3o/zf7vUF5YKgzwiIoKIiIhyy6Kjo8nMzKRNmzYUFRVhGEbZ2ThAQEAAWVlZZa9PnjxJx44d\ncXNzY+rUqQDk5+ezefNmgLLL9AC9evVi7dq1V9GaiIhj+SZjN09tfJzDuWl0q38L88MX6XGrDsyq\nMfLQ0FASEhIASExMpHv37uXe79ChA3v27CE3N5f8/HxSUlLo0qULW7duLbspbvXq1YSFhWEYBsOG\nDSM3NxeA7du307KlptQTEflfpUYpb387lwGf9OFI7mGe7fxXVg1cqxB3cFaNkffv35+kpCQiIyNx\nc3Nj5syZACxYsICuXbvSqVMnxo8fT1TUrw8fGDVqFN7e3nTv3p2lS5cyZMgQ6tSpw+zZs7FYLAwZ\nMoRhw4bh6elJYGAgo0ePrtQmRURs3alzpxi9+Wk2HdmAv2cAb/V+h9sb9zS7LKkBLEZFA9w1UFWM\nhzjSOMvv1LNjcMSewb76Tjq+jeGbojiR/wu3N+rJvN7vEOAVcNF69tTzlXKknq0eIxcREXOUlJYw\ne/crxO6ahQULL94yhWc6Pas5xKUcBbmISA30S146Izb9maT0bTSq3Zh/9HmXrvW7V7yhOBwFuYhI\nDbPp8HpGbx7OqfOn6H/jPczpOZe6Hr5mlyU1lIJcRKSGKCwpZPrXU3k79U3cnNyYEfYaT7R7UjOW\nyWUpyEVEaoC0Mz/z9MbH+eZkCs3rtmBBn8W0vy7I7LLEBijIRURMturASsZvHcvZwlyGtI5kZo9Y\narvWNrsssREKchERkxQUFfDSV9F8sG8xXi61eLPXfB5s87DZZYmNUZCLiJjgx9P7eXLDY+w//QM3\n12vPO30W08JXT7WUq6cfI4qIVCPDMFi67336rLid/ad/4Il2T7Ju0GaFuFhNZ+QiItXkbGEuf90y\nlk8OrqSOe13m3fkOA5rfa3ZZYuMU5CIi1eDbkyk8teFx0nJ/pktgN/7R510aezcxuyyxA7q0LiJS\nhQzD4B+p87j743DScn9mTKdxfDpwnUJcKo3OyEVEqsipc6cY+8UINhxO4DpPf+bduYCeTe40uyyx\nMwpyEZEqkJz+FcM3RvFLfjo9GvVkXu8FBHoFml2W2CEFuYhIJSopLeH13a/y2q6ZWLAQ030SYzqP\n04xlUmUU5CIileRE/i+M3PQk245/ScPajZgf/i7dr7/F7LLEzinIRUQqwebDG3hm89OcOn+Ku268\nmzd6zsPXw8/sssQBKMhFRK5BYUkhf9/+N976Ng43Jzf+ftsrRLV/WjOWSbVRkIuIWOlwbhpPb3ic\nlJO7aVanOe/0WUx7/w5mlyUORkEuImKFdT9/zujNw8ktPMPgVg/ySo/Z1HbzNrsscUAKchGRq7Tw\nu/lM3DYBTxdP4nq9zYOtH9aldDGNglxE5AqVGqW8nDyZed++QYBXIB/eHU+Qf0ezyxIHpyAXEbkC\nF0ouMPaLEXx8YAUt6rZk+YCPaeLT1OyyRBTkIiIVOXMhh8cTHmHb8S/pWr87H/Rfjp9HPbPLEgEU\n5CIil3X87DEe/nwwP5zeR/8b7+Ht8IV4uniaXZZIGT0zUETkEvad2kv/j3vzw+l9/Ln90yzq+75C\nXGocnZGLiPyBbce/5LF1D3O2MJdJt77MqI5jdGe61EgKchGR//HxgXhGbx4OwNu9FzKo1RCTKxK5\nNF1aFxH5jWEYzP3mDYZvjMLDxZN/3fOJQlxqPJ2Ri4jw6/SjL30VzcI9/+D6Wg1YNmAlbevdbHZZ\nIhVSkIuIwztXfI6Rm57k80OraeN3E8vuXklD70ZmlyVyRRTkIuLQTp8/xaNrI9lx4mtCG4SxuN9S\n6rjXNbsskSumIBcRh3Uk9zAPrXmAgzkHuL/FIOLunI+7s7vZZYlcFauCvKioiOjoaNLT03F2dmbG\njBk0bty43Dpnzpxh3Lhx1KpVi7i4uMtut3//fqZMmQJA69atmTp16rV1JSJSgT2ZqUR+PpiTBRmM\n6jiWl26dipNF9/+K7bHqX+2aNWvw8fFh2bJlDB8+nNjY2IvWmTx5MsHBwVe03fTp04mJiWH58uXk\n5eWxdetWa8oSEbkiXxzZxL2r+pFZcJK/3/YKk0NeVoiLzbLqX25ycjLh4eEAhISEkJKSctE606ZN\nuyjI/2i7wsJCjh8/TlBQEAA9e/YkOTnZmrJERCq0fP9SHlk7hOLSIhb2fZ8/Bw03uySRa2LVpfWs\nrCz8/PwAcHJywmKxUFhYiJubW9k6tWvXvqLtsrKy8PHxKVunXr16ZGZmXvbzfX29cHFxtqb0y/L3\n9670fdZ06tkxOGLPUL5vwzCY9uU0Jm2ZhK+HL59FfkZok1ATq6sajnisHbHn/1ZhkMfHxxMfH19u\nWWpqarnXhmFY9eF/tN2V7Cs7u8Cqz7scf39vMjPPVvp+azL17BgcsWco33dxaTETvhzHB/sW09i7\nCcsHfExLz1Z293dxxGPtSD1f6gtLhUEeERFBREREuWXR0dFkZmbSpk0bioqKMAyj3Nn4pQQEBFy0\nnb+/Pzk5OWXrZGRkEBAQUOG+RESuRH5RPk9tGMbGw+tpf10HPrw7nsBa9c0uS6TSWDVGHhoaSkJC\nAgCJiYl0797d6u1cXV1p1qwZu3btAmDDhg2EhYVZU5aISDmZBZk88OndbDy8njsa9+LTgWsV4mJ3\nrBoj79+/P0lJSURGRuLm5sbMmTMBWLBgAV27diUoKIhhw4aRm5tLRkYGQ4cOZeTIkZfcLiYmhkmT\nJlFaWkqHDh0ICQmpvA5FxCEdPH2Quz/uQ1ruzzzY+mFm3/Emrs6uZpclUukshrUD3CaqivEQRxpn\n+Z16dgyO2PPujJ0MXfcgWQVZjAt+jgndXnSIKUgd8Vg7Us9Wj5GLiNiS9WnreGrDMC6UXODV2+fw\n2M1PmF2SSJVSkIuI3Viy910mfDkOd2d3Vj24ilv87jC7JJEqp0cZiYjNMwyDGdv/xnNbn8XX3ZdP\n7vuce1rfY3ZZItVCZ+QiYtMKSwoZt2U0H/24jBt8bmT5PR/TrE5zs8sSqTYKchGxWWcLc3kiYShb\njyXSKaAz/+wfj7+Xv9lliVQrBbmI2KQT+b/w8OcRfJ/1HX2a3sU/+rxHLddaZpclUu00Ri4iNuc/\np3+k/8refJ/1HUPbPs7ifh8qxMVh6YxcRGzK178k8+jaB8m5kEN0txf5S/BzDvEbcZFLUZCLiM34\n7KdPGbnpz5QYJcT1epuH2vzJ7JJETKdL6yJiExakvsWf1z+Ki5Mr/+z/kUJc5Dc6IxeRGq3UKGVq\n0ku8nfomAV6BLLt7Be39O5hdlkiNoSAXkRrrQskFxmwezicHV9KybiuWDVhJE5+mZpclUqMoyEWk\nRjpzIYfH1j1MUvo2utW/hQ/6L8fXw8/sskRqHAW5iNQ4x88eI/LzQew//QN3N7uXt3q/g6eLp9ll\nidRIutlNRGqUvVnf0+/jO9l/+geebD+chX2WKMRFLkNn5CJSY/z72FaGJfyJs4W5TL51GiM7jtZv\nxEUqoCAXkRph5X8+YswXIwCYH76IB1pGmFyRiG1QkIuIqYpKinh996u8tmsmPm51WNxvKbc17GF2\nWSI2Q0EuIqbZeWI7f90ylh9O76NBrYZ8OGAFbevdbHZZIjZFQS4i1e7MhRymfT2V9/e+i4HBo22f\n4KVbp1DHva7ZpYnYHAW5iFQbwzD47KdVxGx7npMFGbT2bcNrd8TR/fpbzC5NxGYpyEWkWhw9e4To\nL8ez8fB63J3deaHbS4zqNBY3ZzezSxOxaQpyEalSxaXFvPPdfGbtmE5BcT5hDW/n1dtfp1ndFmaX\nJmIXFOQiUmVST37D+K1j+S7zW/w8/JjVI5YhrSP123CRSqQgF5FKl1eUx6zt03hnz3xKjVIebP0w\nU0KmU8+zntmlidgdBbmIVKr1aeuI/nI8x/OO0axOc169fQ5hjW43uywRu6UgF5FKcSL/F2L+/Txr\nDn2Kq5Mr44Kf49ng5/Bw8TC7NBG7piAXkWtSapSyeO8ipn89lbOFuXSrfwuxd8TR2q+N2aWJOAQF\nuYhYbd+pvYzfMobdGTvxcavDa7e/wSNtH8PJookVRaqLglxErtq54nPE7pzFW6lxFJcWM7DFA7x8\n2ywCvQLNLk3E4SjIReSqbDn6Bc9tfZbDuWk09m7CKz1mc2fTPmaXJeKwFOQickUyCzKZ9NULrDzw\nEc4WZ0Z1HMtfu0ZTy7WW2aWJODQFuYhclmEYLNv/T6YkTSTnQg6dAjrz2h1xtL8uyOzSRAQrg7yo\nqIjo6GjS09NxdnZmxowZNG7cuNw6Z86cYdy4cdSqVYu4uLjLbjd06FAKCgrw8vICYMKECbRr1+4a\nWxORa3Uw+wB/3TqWpPRt1HKtzd9ve4XH2z2Js5Oz2aWJyG+sCvI1a9bg4+NDbGws27ZtIzY2ljlz\n5pRbZ/LkyQQHB7N///4r2m7GjBm0atXqGloRkcpyoeQCcSmzeWN3LIWlhfS7cQAzwl6lQe2GZpcm\nIv/Dqt+IJCcnEx4eDkBISAgpKSkXrTNt2jSCg4OvejsRMVdy+lf0+lcor+6cQT3P63jvrqUs6feh\nQlykhrLqjDwrKws/Pz8AnJycsFgsFBYW4ub2/9MR1q5d+4q3A4iLiyM7O5vmzZsTExODh8elnwbl\n6+uFi0vlX9rz9/eu9H3WdOrZMVxJz6fPneb5jc+z6JtFWLDwTNdnmH7ndHzcfaqhwqqhY+0YHLHn\n/1ZhkMfHxxMfH19uWWpqarnYa6RwAAAcCklEQVTXhmFY9eG/b/foo4/SunVrmjRpwuTJk1m6dClR\nUVGX3C47u8Cqz7scf39vMjPPVvp+azL17Bgq6tkwDD4+EM9LX71A1rlM2tZrR+wdbxAc2JULuZCJ\nbf69dKwdgyP1fKkvLBUGeUREBBEREeWWRUdHk5mZSZs2bSgqKsIwjHJn45cSEBDwh9v9frkdoFev\nXqxdu7bCfYnItfv5zCEmfDmOLUe/wNPFk0m3vszTQSNxdXY1uzQRuUJWjZGHhoaSkJAAQGJiIt27\nd7d6O8MwGDZsGLm5uQBs376dli1bWlOWiFyhopIi4lJmc/vyW9hy9At6NenNlw9t55lOYxXiIjbG\nqjHy/v37k5SURGRkJG5ubsycOROABQsW0LVrV4KCgsrCOSMjg6FDhzJy5Mg/3M5isTBkyBCGDRuG\np6cngYGBjB49ulKbFJH/t+vEDsZvGcsPp/dynac/b9z2FgNbDMJisZhdmohYwWJYO8BtoqoYD3Gk\ncZbfqWfH8HvPuRfOMH37VBZ/vwgDg6Fth/HSLVOp6+FrdolVwpGPtSNxpJ6tHiMXEdtmGAaf/fQp\nE7c9z4n8X2jl25rXbn+DWxqEmF2aiFQCBbmIHTt+9hhRmybw2X8+w83JjQndJvJMp2dxd3Y3uzQR\nqSQKchE7VFJawsI985mxfRoFxfmENgjjtTvm0LyubiQVsTcKchE7UlBUwM4T25n29RRSM7/B192X\neXfPpX+DB3Qzm4idUpCL2KhSo5RDOT+xK2MHKRm72J2xi32nvqfEKAEgotVDTA39Ozc1udFhbgYS\ncUQKchEbkX3+dFlg787YyTcnd5NzIafsfXdndzoHdqFzYBf63ziAWxuEmlitiFQXBblIDVRUUsS+\nU9+z++Qudp/Yye6MnRw681O5dW6s04zeTfsSHNiF4MCutK3XDjfnip+wKCL2RUEuYjLDMEjPO87u\njJ1lZ9vfZX7L+ZLzZev4uNXhjsa96BzYhS6BXekU0IV6nvVMrFpEagoFuUg1yy/KJ/XkN+XOtjMK\nTpS972Rxom29dgQHdi07225etwVOFqueqCwidk5BLlKFSo1SDmYfKHe2vf/0vrIb0gACvepzd7N7\ny862g/w7Usu1lolVi4gtUZCLVKJT506RkrGz7Gz7m5Mp5BaeKXvfw9mDLvW70TmgC13qd6VzQBca\n1G6on4aJiNUU5CJWKiwpZG/WnnJn22m5P5dbp3ndFvS9oR/B9bvSJbArN/ndrNnFRKRSKchFroBh\nGBzLO/rrmPZvZ9t7slK5UHKhbJ267nXp1aR32dl2p4BgfD38TKxaRByBglzkEo6fPcZnh1aRlP4V\nu0/sJPPcybL3nC3O3HxdezoHBP92U1pXmtVtrhvSRKTaKchF/svJgpN89tMqVh1cyfZfksuWN6jV\nkAHN7iu7kzzIvyNerl4mVioi8isFuTi87POnWXtoDZ8cXMm241spNUqxYOG2hj0Y2GIQvZv2oUHt\nhmaXKSLyhxTk4pDyCs+SkLaWVQdWknh0M0WlRQB0CezG/S0HcU/zgdSvdb3JVYqIVExBLg7jXPE5\nVu7bwJKUf7IxLaHsyWntr+vAwJaDuK/5/TTxaWpylSIiV0dBLnatsKSQrUe/4JODK1n38+fkF+UB\n0LJuKwa2HMT9LQbTwldzdIuI7VKQi90pKS3hq/R/s+rAStYc+rRshrAm3k0Z3e0Z+jS8h5vrtdND\nWETELijIxS6UGqXsPLGDVQdXsPrgqrKfitWvdT1Pt/kT97cYRKeAYAICfDQ3t4jYFQW52CzDMPgu\n81s+ObiSTw9+zPG8YwDU86jHYzdHcX+LQdzSIES/7RYRu6YgF5uz//QPrDqwgk8OruTnM4cA8Hbz\n4aE2f2Jgi0GENbxdj0EVEYehIBebcOjMT3x64GNWHVzJD6f3AeDl4sX9LQYxsOVgejXpjbuzu8lV\niohUPwW51FjHzx7j058+YdWBFXyb+Q0Abk5u9LtxAPe3GET4DXdpuk8RcXgKcqlR/ugRqc4WZ3o1\n6c3AFoPof+MAfNzrmFyliEjNoSAX0+Wcz+bzQ59d9IjU0AZhDGw5iAHN7qOeZz2zyxQRqZEU5GKK\nSz0iNTiwK/e3GMS9Le7XI1JFRK6Aglyqzbnic2w6vIFVB1eWe0Rqu+uCGNhiEPe1uJ+mPjeYW6SI\niI1RkEu1+PzQZ/x1yxhOnT8FQIu6Lbm/5WAGthhES99WJlcnImK7FORSpfIKzzJx2wSW7f8nHs4e\njOo4lkGthugRqSIilURBLlVmxy/bGbX5SQ7nphHk35G37nyHVn6tzS5LRMSuWPXsyqKiIsaPH09k\nZCSPPPIIR48evWidM2fOEBUVxZgxY8ot37FjB7feeiuJiYlly/bv389DDz3EQw89xOTJk60pSWqQ\nopIiZm5/mXtX9eVI7mHGdh7P2gc2KcRFRKqAVUG+Zs0afHx8WLZsGcOHDyc2NvaidSZPnkxwcHC5\nZUeOHOG9996jc+fO5ZZPnz6dmJgYli9fTl5eHlu3brWmLKkBDmYf4O6PezN796s0rN2ITweuY+It\nk3FzdjO7NBERu2RVkCcnJxMeHg5ASEgIKSkpF60zbdq0i4Lc39+fuXPn4u3tXbassLCQ48ePExQU\nBEDPnj1JTk62piwxkWEYvPf9Qu6Mv41vM7/hwdYPs+XBJG5pEGJ2aSIids2qMfKsrCz8/PwAcHJy\nwmKxUFhYiJvb/5911a5d+6LtPD09L1qWnZ2Nj49P2et69eqRmZl52c/39fXCxcXZmtIvy9/fu+KV\n7Exl9Hwi7wRRq6NYe2Atfp5+vH//+wxuO7gSqqsaOs6OwxH7Vs+Op8Igj4+PJz4+vtyy1NTUcq8N\nw6i0gq5kX9nZBZX2eb/z9/d2uHmqK6PndT9/zrjEZzh1/hS3N+rJm3fOp36t62vs31LH2XE4Yt/q\n2b5d6gtLhUEeERFBREREuWXR0dFkZmbSpk0bioqKMAyj3Nn41fDz8yMnJ6fsdUZGBgEBAVbtS6pP\nXlEeL22LZukP7+Pu7M7022YR1f5pzf0tIlLNrPqvbmhoKAkJCQAkJibSvXt3qwtwdXWlWbNm7Nq1\nC4ANGzYQFhZm9f6k6u08sZ1e/wpl6Q/v0+66IDZGfMmTQSMU4iIiJrBqjLx///4kJSURGRmJm5sb\nM2fOBGDBggV07dqVoKAghg0bRm5uLhkZGQwdOpSRI0dy4cIFFi1axKFDh9i7dy8ffPAB7777LjEx\nMUyaNInS0lI6dOhASIhukKqJikqKmL37FV7f/SqGYTC60194vluM5gEXETGRxajMAe5qUhXjIY40\nzvK7q+n5p5wDjNz0JN+cTKFR7cbM672AWxuEVnGFlU/H2XE4Yt/q2b5ZPUYujs0wDN7f9x6Tv4qh\noLiAiFYPMSPsVc0JLiJSQyjI5ZJOFpxkXOIzbDicQB33uizoOY+BLQeZXZaIiPwXBbn8ofVp6/hL\n4iiyzmUR1ugO3uz1Ng1qNzS7LBER+R8KciknvyifSV/F8MG+93B3dufl0Bm6I11EpAZTkEuZ3Rk7\nGbnpSX4+c4i29drxdu+F3FSvrdlliYjIZSjIheLSYl7f/Sqzd71CqVHKyI5jeKH7S/pZmYiIDVCQ\nO7hDZ35i1KYn2Z2xi4a1G/HmnfO5rWEPs8sSEZErpCB3UIZhsDBlIWPXPUtBcT4PtIxgVo9Y6rjX\nNbs0ERG5CgpyB5RZkMn4LaNJSFuLj1sd5ocv4oGWERVvKCIiNY6C3MFsTEtgbOIoss5l0vOGnswO\nm0dD70ZmlyUiIlbSb4ocRH5RPs9t/Qt/WjuE3AtnmBIynU2PblKIi4jYOJ2RO4BvMnYzcvOT/JRz\nkJv82vJW74XcfF07/TZcRMQOKMjtWHFpMW+kxBK7axbFpcUM7/AMMd0n4eHiYXZpIiJSSRTkdurn\nM4cYtekpdmXs4PpaDXjzzvn0aHSH2WWJiEglU5DbGcMwWLb/n0zcNoH8ojwGtniAV3q8Tl0PX7NL\nExGRKqAgtyNZ57IYv2UM635eg49bHd7q/Q6DWg7BYrGYXZqIiFQRBbmd2Hx4A2O+GEnmuZOENLiN\nuXf+g0bejc0uS0REqpiC3MYVFBUwNflF3vt+Ia5Orky69WVGdHgGZydns0sTEZFqoCC3Yaknv2HE\npj9zMOcAbfxuYl7vd2h/XZDZZYmISDVSkNsgwzCIS5nNrJ3TKS4t5qmgEUy8ZQqeLp5mlyYiItVM\nQW5jDMNgStKLvJ36JvVrXU9cr7e5o3Evs8sSERGTKMhtzOzdr/B26pu0rNuKVQPX4e/lb3ZJIiJi\nIj2j04YsSH2LWTum08TnBlbcu1ohLiIiCnJb8eEPH/DiV9EEetVnxT2fcn3tBmaXJCIiNYCC3AZ8\nevBjxm0ZjZ+HH/H3fsoNdW40uyQREakhFOQ13KbD6xmx6c94udTiXwM+oY3fTWaXJCIiNYiCvAZL\nOr6NJxKG4urkyod3x9MhoJPZJYmISA2ju9ZrqJSMXfxp7RBKjBI+6LecWxqEmF2SiIjUQAryGmjf\nqb08tOYBzhUX8E6fJfRqEm52SSIiUkMpyGuYQ2d+ImL1feRcyCGu19vc0/w+s0sSEZEaTGPkNcjx\ns8eIWH0fmedO8vfbXuGhNn8yuyQREanhFOQ1RGZBJoM/u5ejZ48Q030Sfw4abnZJIiJiAxTkNUDO\n+WyGfDaQn3IO8kynZxnbebzZJYmIiI2wKsiLiooYP348kZGRPPLIIxw9evSidc6cOUNUVBRjxowp\nt3zHjh3ceuutJCYmli0bOnQogwYNYujQoQwdOpTvv//emrJsUl5RHg9/HsHeU3t47OYoXrplKhaL\nxeyyRETERlh1s9uaNWvw8fEhNjaWbdu2ERsby5w5c8qtM3nyZIKDg9m/f3/ZsiNHjvDee+/RuXPn\ni/Y5Y8YMWrVqZU05Nut88XkeW/cwuzJ2MLjVg8zqEasQFxGRq2LVGXlycjLh4b/+JCokJISUlJSL\n1pk2bRrBwcHllvn7+zN37ly8vb2t+Vi7UlRSxFMbhvHvY1u468a7iev1Nk4WjXSIiMjVseqMPCsr\nCz8/PwCcnJywWCwUFhbi5uZWtk7t2rUv2s7T0/OS+4yLiyM7O5vmzZsTExODh4fHJdf19fXCxcXZ\nmtIvy9+/er5glBqlDP1kKAlpa+ndrDefRK7Aw+XS/Val6uq5JlHPjsMR+1bPjqfCII+Pjyc+Pr7c\nstTU1HKvDcO4piIeffRRWrduTZMmTZg8eTJLly4lKirqkutnZxdc0+f9EX9/bzIzz1b6fv+XYRg8\nt/UvfLjvQ7rW7847d37A2ewizlJU5Z/9v6qr55pEPTsOR+xbPdu3S31hqTDIIyIiiIiIKLcsOjqa\nzMxM2rRpQ1FREYZhlDsbv1q/X6YH6NWrF2vXrrV6XzWZYRhMTX6J9/e9S7vrgvjw7nhqudYyuywR\nEbFhVg3KhoaGkpCQAEBiYiLdu3e3ugDDMBg2bBi5ubkAbN++nZYtW1q9v5rs9d2v8ta3cbSo25J/\nDfiEOu51zS5JRERsnFVj5P379ycpKYnIyEjc3NyYOXMmAAsWLKBr164EBQWVhXNGRgZDhw5l5MiR\nXLhwgUWLFnHo0CH27t3LBx98wLvvvsuQIUMYNmwYnp6eBAYGMnr06EptsiZ457u3mbljGo29m7Di\n3tX4e/mbXZKIiNgBi3GtA9wmqIrxkKocZ1n2wz8ZmziSAK9AVt+fQLM6zavkc66WI40t/U49Ow5H\n7Fs927dLjZHr905VbPXBT/jLlmfwdfcl/p5Pa0yIi4iIfVCQV6HNhzcwYtOf8XKpxfIBH3NTvbZm\nlyQiInZGQV5Fko5v4/GER3C2OLP07o/oFBhc8UYiIiJXSfORV4FvMnbzyNoHKTFKeL/fMm5tEGp2\nSSIiYqcU5JXsh1P7eGjNAxQU57Mg/D3ubNrH7JJERMSOKcgr0aEzPxHx2X1kX8jmjZ5vcW+L+80u\nSURE7JzGyCtJet5xIlbfx8mCDKbfNovImx4xuyQREXEACvJKkFmQyeDV93L07BGiu73Ik0EjzC5J\nREQchIL8Gp25kMODa+7nYM4BRnUcy1+CnzO7JBERcSAK8muQV5RH5JrBfJ/1HY+2fYJJt/4Ni8Vi\ndlkiIuJAFORWOl98nmHr/sSujB080DKCWT1iFeIiIlLtFORWKCop4qmNj/PlsUTuuqE/b/aaj7OT\ns9lliYiIA1KQX6VSo5QxX4wg4efPCWt0Bwv6LMbV2dXsskRExEEpyK+CYRhM+HI8Kw98RHBgV5b0\n+xAPFw+zyxIREQemIL9ChmHw8teTWbJ3ETfXa8+yu1dQ27W22WWJiIiDU5BfoTdSYpn7zRya123B\nR/esoq6Hr9kliYiIKMivxMLv5vP37X+jUe3GrLhnNf5e/maXJCIiAijIK7R8/1Jitj1PgFcgK+5b\nTUPvRmaXJCIiUkZBfhmf/fQpzyaOoq57XT66ZxXN6jQ3uyQREZFyFOSX8MWRjQzf+ASeLl4sH/Ax\nbevdbHZJIiIiF1GQ/4Gv05N4POERnC3O/LP/v+gc2MXskkRERP6Q5iP/H9+eTOHhzyMoKi3i/X7L\nCG0YZnZJIiIil6Qg/y/7T//AQ2seoKA4n3+Ev0vvpn3NLklEROSyFOS/+en0T0Ssvo/T508zp+c8\n7mvxgNkliYiIVEhj5EB63nF6f9CbjIITvBw6g4dvGmp2SSIiIlfE4YO8oKiAiNX3kZaTxvNdY3i6\nwyizSxIREbliDn9pPetcJsfyjjIhdALjgiaYXY6IiMhVcfggb+LTlINRx2hQ34/MzLNmlyMiInJV\nHP7SOqD5xEVExGYpyEVERGyYglxERMSGKchFRERsmFU3uxUVFREdHU16ejrOzs7MmDGDxo0bl1vn\nzJkzjBs3jlq1ahEXFwdAcXExEydO5MiRI5SUlPD888/TpUsX9u/fz5QpUwBo3bo1U6dOvbauRERE\nHIRVZ+Rr1qzBx8eHZcuWMXz4cGJjYy9aZ/LkyQQHB5db9umnn+Lp6cmyZcuYPn06M2fOBGD69OnE\nxMSwfPly8vLy2Lp1qzVliYiIOByrgjw5OZnw8HAAQkJCSElJuWidadOmXRTk9957Ly+88AIAfn5+\n5OTkUFhYyPHjxwkKCgKgZ8+eJCcnW1OWiIiIw7Hq0npWVhZ+fn4AODk5YbFYKCwsxM3NrWyd2rVr\nX7Sdq+v//8xryZIlDBgwgOzsbHx8fMqW16tXj8zMzMt+vq+vFy4uztaUfln+/t6Vvs+aTj07Bkfs\nGRyzb/XseCoM8vj4eOLj48stS01NLffaMIyr+tClS5eyd+9e5s+fz+nTp696X9nZBVf1eVfC39/b\n4R4Io54dgyP2DI7Zt3q2b5f6wlJhkEdERBAREVFuWXR0NJmZmbRp04aioiIMwyh3Nn458fHxfPHF\nF7z11lu4urqWXWL/XUZGBgEBAVe0LxEREUdn1Rh5aGgoCQkJACQmJtK9e/cr2u7o0aMsX76cuXPn\n4u7uDvx6ub1Zs2bs2rULgA0bNhAWFmZNWSIiIg7HqjHy/v37k5SURGRkJG5ubmV3ny9YsICuXbsS\nFBTEsGHDyM3NJSMjg6FDhzJy5EiSk5PJycnhqaeeKtvXokWLiImJYdKkSZSWltKhQwdCQkIqpzsR\nERE7ZzGudoBbREREagw92U1ERMSGKchFRERsmIJcRETEhinIRUREbJiCXERExIYpyEVERGyYglxE\nRMSGWfVAGFti7dzpl9rOFuZOv5KeV69ezZIlS3BycmLIkCFERERQUFBAdHQ0WVlZeHp6MnPmTPz9\n/Rk6dCgFBQV4eXkBMGHCBNq1a2dGa5dU2T3b83HOyMggJiaGwsJCSktLeeGFF2jXrh29evWifv36\nODv/OiHRa6+9RmBgoBmtXVZl952UlMTs2bNxdnamR48ejBo1yqTOLs3ant9++22SkpIAKC0tJSsr\ni/Xr19vEsa7snm3hOFvNsHMff/yxMWXKFMMwDOPf//63MXbs2IvWGTt2rDFv3jxj9OjRFW73yCOP\nGKmpqYZhGMa4ceOMLVu2VHULV62invPz840+ffoYubm5xrlz54y7777byM7ONt577z3jlVdeMQzD\nMHbu3Gm8+OKLhmH82vOPP/5YvU1cparo2V6P88yZM41ly5YZhmEYu3fvNp544gnDMAyjZ8+eRl5e\nXvU2YYXK7rtfv35Genq6UVJSYkRGRhoHDhyo3oaugLU9/+8+3nnnHcMwbONYV3bPtnCcrWX3l9at\nnTv9j7azlbnTK+o5NTWV9u3b4+3tjYeHB507dyYlJYW0tLSy3rp06cLu3burvXZrVWbP9n6cfX19\nyyYqys3NxdfXt9prvxaV2ffRo0epU6cO119/PU5OTtx+++12dax/V1xczLJly3jkkUeqte5rUZk9\n28pxtpbdX1q3du70P9ouKyvrqudON0NFPf/3+wB+fn5kZmbSqlUrtm7dSt++fdmxYwfp6ell68TF\nxZGdnU3z5s2JiYnBw8OjepuqQGX2nJ2dbdfHediwYQwePJhVq1aRl5fHsmXLytaZPHkyx48fJzg4\nmPHjx2OxWKq3qStQmX1nZmZetO7Ro0ert6ErYG3Pv9uwYQO33XZbuf/f1vRjXZk928pxtpZdBXlV\nzJ1+ue2s3Vdlqoyef39/8ODB/Pjjj0RGRtKtW7eyf/iPPvoorVu3pkmTJkyePJmlS5cSFRVViV1c\nnero+Wr2VR0qs+eFCxfSr18/RowYQWJiIrNmzWLu3LmMGTOGsLAw6tSpw6hRo1i/fj133XVX5TZy\nlaq67yeeeKJyC64Eldnz71auXFnuPo+adqyro2d7ZldBXplzpwcEBFy0nb+/f42bO92angMCAsjK\nyip7ffLkSTp27Iibm1vZP/z8/Hw2b94MUHZ5C6BXr16sXbu2KluqUFX37OfnZ9fHeePGjTz77LPA\nr1MS/97/wIEDy9bt0aMH//nPf0wP8qru+3/XtbdjDVBQUMCJEydo1KhR2fs17VhXdc818ThXJrsf\nI7d27vQ/2s5W5k6vqOcOHTqwZ88ecnNzyc/PJyUlhS5durB161bmzJkD/Ho3aFhYGIZhlE1JC7B9\n+3ZatmxZvQ1dgcrs2d6Pc9OmTcvOdr777juaNm3K2bNniYqKorCwEICdO3fWyOMMldt3o0aNyMvL\n49ixYxQXF5OYmEhoaGi191QRa3sG2L9/P82aNStb11aOdWX2bCvH2Vp2P41pSUkJL774ImlpaWVz\np19//fWXnDu9ZcuWjBw5km7duv3hdgcPHiw3d/oLL7xgdosXqajnTp06kZCQwKJFi7BYLDzyyCPc\ne++9nD9/njFjxpCTk0OdOnWYPXs23t7erF27loULF+Lp6UlgYCDTp0/H09PT7DbLqeye7fk4nzx5\nkokTJ3L+/HkAJk6cSJs2bViyZAmrVq3C3d2dtm3b8tJLL9W4cVOo/L537tzJa6+9BkCfPn1MHTa6\nFGt7Bsp+evXfl5lt4VhXds+2cJytZfdBLiIiYs/s/tK6iIiIPVOQi4iI2DAFuYiIiA1TkIuIiNgw\nBbmIiIgNU5CLiIjYMAW5iIiIDfs/3puVT4/t4/QAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 88
+ },
+ "outputId": "3bd3bcca-54e3-435e-b0e4-cc4be7b67475"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 19,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.\n",
+ "Instructions for updating:\n",
+ "Colocations handled automatically by placer.\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 88
+ },
+ "outputId": "e7c422ef-e885-4474-ad28-73f76da5b5ce"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 21,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.\n",
+ "Instructions for updating:\n",
+ "Use tf.cast instead.\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "outputId": "4e61336a-d3df-4140-cfab-7e14818eb815",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 432
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 22,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.17406574\n",
+ "Loss after epoch 20 is 0.17394462\n",
+ "Loss after epoch 40 is 0.17382358\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.0014628248\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFKCAYAAAAwrQetAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3XdcleX/x/HXfQZLliA4MBduFDeK\npobi3g0zs6W5texXXy3K1CxHqZVaZqVlaUWZfrOlpplpIDhxL1TcLBHZcM65f39AN/lNxQEczuHz\nfDx85OE64/MJ9c1939d9XYqqqipCCCGEKPN01i5ACCGEELdHQlsIIYSwERLaQgghhI2Q0BZCCCFs\nhIS2EEIIYSMktIUQQggbYbB2AbeSmJhm7RKoWNGFlJRMa5dRYqQ/22bv/YH99yj92b7i7tHHx+2m\nY3KkXQSDQW/tEkqU9Gfb7L0/sP8epT/bV5o9SmgLIYQQNkJCWwghhLAREtpCCCGEjZDQFkIIIWyE\nhLYQQghhIyS0hRBCCBshoS2EEELYiDK9uEpZtGjRuxw7doQrV5LJzs6mWjU/3N09mDXrnWJ5/4cf\n7oevb2V0usKfpxYv/vie33f79q20bduea9dSWbZsKZMnv3rP7ymEEKJ03VZoHz9+nHHjxvH0008z\nbNiw68YiIiJYsGABer2eTp06MX78eABmzZpFTEwMiqIQFhZGYGAgly5dYvLkyZjNZnx8fHjnnXdw\ncHAo/q5K0MSJLwDwyy8/cupULBMmTCr2z5g3byEuLi7F+p7ffLOKli3b4O1dSQJbCCFsVJGhnZmZ\nycyZMwkODr7h+JtvvsmyZcuoXLkyw4YNo0ePHly5coW4uDjCw8OJjY0lLCyM8PBwFi5cyNChQ+nV\nqxcLFixg9erVDB06tNibsoY9e3bxzTcryczMZMKEF3jxxQn8/PNmAF57bTIPPjiYhg0bMWvWDNLS\n0jCbzUya9B/q1q13W+/fp0/Xf73f3r27ychI5+zZOC5cOM9zz71IcHAH1q//mdWrw1EUhSFDHicv\nL4/Dhw/y0kvP8fLLU5kx4zWWLfuSPXt28dlnS1FVBR8fX1555XU2bdrA/v37uHo1hbNn4xg69An6\n9h1YYv/fhBBC3L4iQ9vBwYFPPvmETz755F9j586dw8PDg6pVqwLQuXNnIiMjuXLlCqGhoQD4+/uT\nmppKeno6UVFRzJgxA4CQkBCWL19+T6E9PeI1foz9712//kb6+Q9kevs37+q1sbEn+frrNTc9e/Dt\nt1/Ttm17+vUbyOnTp3j//Xm8996H91IuCQnxzJu3kB07Ivjhh+9p1qw5n3/+KStWfE1ubh5vvTWN\nOXMW8OmnHzFv3kJSU69qr503bzZffLECg8GVBQvm8ttv61EUhdjYk3z00XLOnz/HtGlhEtpCCHED\nmXmZ/HTqB55wHwIopfKZRYa2wWDAYLjx0xITE/Hy8tIee3l5ce7cOVJSUggICLju64mJiWRlZWmB\n5u3tTWJi4i0/u2JFl1uu6eri7IBOV7z/o1ycHf61WPuNFm93c3PCxaXwuZ6eLjRu3Ag/P28AFEXR\nxhwdjXh6unDs2CGuXLnCli0bAcjJyfrXe+v1Ol555QX0+vy+K1asyMKFC2/4fhUqOBIc3BYfHzca\nNKhNTk4WqakJ1KtXl+rVfQBYtuwT7X0rVXJFr8/DYNBhNJoxGPTaD1wPPNCRnTt30rhxY9q0aUWV\nKp64uRnJysq45eL1tsDW6y+KvfcH9t+j9Gd7UrJSGPr1g0Sci6CylxcPN364VD63VCaiqap6W1/7\nX0XtmjK5xetMbvH6Xdd1M//cXczHx+2Gu42lpWWTmZmrjV29momqKtpjVVW132dkZGnjEye+SJMm\ngTf8LACz2cLs2e9ed007MTHthu+XkZGD0ehMYmIaKSkZ5OaaSE3NJjs794bvm5SUTmpqBiaTheTk\nDEwms/b+ycnXyM42kZaWTW6uhcTENDIzMzGbLWVit7W7dbPvn72w9/7A/nuU/mzP5YxLPPrjII5c\nOcyD9R5mQIMBxdpjie3y5evrS1JSkvY4Pj4eX1/ff309ISEBHx8fXFxcyM7Ovu659kpRFLKzs8nO\nzub48WMANG7chD///AOA06dP8c03K+/p/W6kZs1anD0bR2ZmJjk5OUyaNA5VVVEUHWazWXueu7s7\niqJw8eJFAPbt20PDho3uolMhhCg/TqXG0ndtD45cOcyIpqP4MPRTjHpjqX3+PYV29erVSU9P5/z5\n85hMJrZs2UKHDh3o0KEDGzZsAODQoUP4+vri6upK+/btta9v3LiRjh073nsHZdTAgQ8zatRTzJo1\ngwYN8sPw4Ycf5cKFc4wb9yxz575J8+Yt7+n9bsTZ2ZkRI8YwadI4Jk4cTb9+A1EUhRYtWjJu3Ijr\nrmlPnvwaL774IhMmjMJkMtG1a/e7b1gIIezcwaQD9FvTg7PXzvCfNq8w6/530Cmlu9yJohZxnvrg\nwYPMnTuXCxcuYDAYqFy5Ml26dKF69ep069aNnTt3Mm/ePAC6d+/OiBEjAJg3bx67du1CURSmTZtG\nw4YNSUhIYMqUKeTk5FCtWjVmz56N0Xjzn1DKwikVezy180/Sn22z9/7A/nuU/mzDjosRDPvlUa7l\npjK74zuMaDpaGyvuHm91erzI0LamsvCNtpc/cDcj/dk2e+8P7L9H6a/s23jmV57d8BQm1cSiLh/x\nUP3B142XZmjLimhCCCHKpUNJBzly5RCejp54OHri6Vix4L+eOOjz73T69tjXPP/7OBz0DnzZ8xu6\n1rTuZUQJbSGEEOWKqqp8uG8Rb+6Yhlk13/A5LgYXPBw9uZRxEQ9HT1b1/o6gqm1LudJ/k9AWQghR\nbqTnpjFpywTWxa6lsksVJraYRLY5m6s5V0nNucrVgl9//75ppWYs6voRjb0Din7zUiChLYQQolw4\nmXKCZ9Y/zrGUo7StGsyn3VdQuUIVa5d1R2RrTiGEEHbvl1M/0X31AxxLOcqowLGs6f+TzQU2yJH2\nHbt06SJPPjmEBg0aApCbm8vjjz9F584hd/xe338fztWrV+nU6QH+/PMPRowYfcPn/b2t5q1uj/vb\nqVMnWbDg7X9t59m5c1uaNm2mPfb29mbGjNl3XPP/2rJlEyEhoZw4ceyWPQghhDWYLWbmRL/J+3vm\n42xwZknop/+a/W1LJLTvQo0aNbVQvHYtlWeeeZx27YJxdHS6q/erV68B9eo1uOn439tq3k5o34yr\nq2ux7Mv9v1auXEFISGiRPQghRGm7kp3M6I3D2Xp+C7Xca/NZz1UEVGpi7bLuiYT2PXJ398DbuxLJ\nycl89tknGAxGrl27yhtvzOHtt9/i4sULmEwmnn12DK1atWHXrmgWLpyPl5c33t6VqFbNjz17drFm\nzbe8+ebbt9xW8/33l7Bu3Vo2bVqPoujo2PEBHntsGAkJ8Uyd+jJGo5G6devfdu2XLl1k9OhXWLp0\nBQAjRjzBm2/OZfnyj6lUyYdjx44QH3+Z119/kwYNGrJq1Qr++GMziqJjzJgJHD16mJMnjxMW9h8e\nfvhRrYfNm38jPHwVer2eBg0aMWnSSyxbtvSG24gKIURJOJC0n6d/Hcq5tLN0q9mDD7p+jKdTRWuX\ndc9sOrQrTH8Nxx+Ld2vOnH4DyZh++1tzXrp0kWvXUvH1rQzkr+k9ZcqrrF//M97elXjllde5evUq\nzz8/hhUrvmHp0sVMnTqTevXq89JLz1Gtmp/2XpmZGbfcVjMxMYE//tjMhx8uA2Ds2BGEhISyZk04\nXbt2Z/Dgx1i58nNOnjx+z/8fcnNzWbBgMf/972rWr/8ZFxcX/vhjM0uXfs7FixdYufJzXn55KqtW\nrWDWrHfYs2dXQQ+ZfPzxB3z22Ve4uLgwefIL2tj/biMqoS2EKAnrTq7lud/HkmnK5KXWL/NSm5dL\nfbnRkmLToW0tZ8/GMWHCKCB/v/HXXpuhbV/auHH+bQEHD+4nJmYv+/fvAyAnJ4e8vDwuXbpEvXr5\nR8PNm7ckJydHe98zZ05To0YtHB2dcHR0Ys6cBdd97pEjhzh//hwTJ+ZfN87MzODy5YucOXOakJD8\n/ctbtGjNjh0R/6o5PT1dqxnA378uQ4YMu2mPzZq1AMDHpzKHDx/i+PFjNG7cBJ1OR/Xq9/Hyy1Nv\n+Lpz585SvXoNbZeyFi1acfz4UQACA5sD+RvNpKen3/SzhRDiblhUC29Hv8WC3e9QwejKil5f06t2\nH2uXVaxsOrQzpr95R0fFxeWf17T/l8Fg1P775JPD6dat53XjOl3hT3v/u4KsTqdHVS03/VyDwUhw\ncAcmT371uq+vWrUCpeCnyJu9/kbXtC9fvnTdY5PJpP3+7/28/65Tr9dhsRS94q2iXN+XyZSHo6Pj\nDd9TCCGKS1ruNcZvGsX6M79Q070WX/T6hkbeja1dVrGzj/MFZVDjxk3Yvn0rACkpV1i69AMAKlXy\n4ezZM6iqyt69u697TVHbajZo0Ig9e3aTnZ2Nqqq89948cnKyqVGjJkePHgbQTkXfDheXCiQnJ6Oq\nKsnJSVy8eP6mz23QoBEHDsRgMpm4ciWZV155CeBfQX7ffTU5f/4smZkZAOzdu4cGDezvL44Qouw4\nnXqK3t+Hsv7ML3Ss/gAbHt5il4ENNn6kXZZ16RLKnj07GTNmOGazmeHD809Njxo1jtdem0KVKlW1\n6+B/++e2mgCPPjr0um01Fy36mMGDH2P8+JHodDo6dXoAR0cnHnnkMaZOfZk//9yCv3+9267R3d2d\n9u3b8+yzT1K3br1bzv6uWrUaPXr0ZsKEUaiqyujR4wGoX78BI0c+ydixz2k9jB//PC++OBFF0REY\n2JxmzZqza1fUHf3/E0KI27H13BZGbnyKqzlXGRU4lunt38Kgs99ok12+imAPO9TcivRn2+y9P7D/\nHqW/u6OqKh/v/5BpEa9iUAy80/k9Hmt083k6JUl2+RJCCCFuQlVVpke8xpKYRfg4+/J5r1W0qWL9\nzTxKg4S2EEIIm6GqKrOi3mBJzCLqedbnu/4/UM3Vr+gX2gkJbSGEEDZj3q45vL9nPrU96vD9gB+p\nUqGqtUsqVTJ7XAghhE1YuGcB7+ycTQ33Wqzp/1O5C2yQ0BZCCGEDPopZzJs7puPnWp01/X/Ez626\ntUuyCgltIYQQZdqyAx/z+l9hVKlQle8H/EgN95rWLslqJLSFEEKUWV8e/pxXtr2Ej7Mv3/f/kToe\n/tYuyaoktIUQQpRJ3xxdxUt/PI+3kzffD/iRehVvfxdDeyWzx4UQQpQpp66eZM2J1czbNQcPRw++\n67+Ohl6NrF1WmSChLYQQwqosqoW9CbtZf/oX1p/+mWMp+TsDejh68m2//9KkUlMrV1h2SGgLIYQo\ndTnmHLaf38qvp39hw5lfiM+8DICT3ometXrTs3YfetTqjbezt5UrLVsktIUQQpSqP879zsTNY7Sg\n9nLyYkjDx+lZqw+d7wuhgrGClSssuyS0hRBClIpccy5zot9k8d73MOgMjGw6hr7+A2hTpa1d78xV\nnOT/khBCiBJ3KjWWMRuHsy9xL7U96rC023Ka+7a0dlk257ZCe9asWcTExKAoCmFhYQQGBmpjmzZt\nYsmSJTg4ONCnTx+GDRvGd999x7p167TnHDx4kL179/LEE0+QmZmJi4sLAFOmTKFJkybF3JIQQoiy\n5NtjXzPlzxfJyEtncIPHmNNxHq4ON99+UtxckaEdHR1NXFwc4eHhxMbGEhYWRnh4OAAWi4WZM2ey\ndu1aPD09GTlyJKGhoTzyyCM88sgj2ut//fVX7f1mz55N/fpyr50QQti7tNxr/N/acazcvxJXoxsf\nhn7Cw/UftXZZNq3IxVUiIyMJDQ0FwN/fn9TUVNLT0wFISUnB3d0dLy8vdDod7dq1IyIi4rrXf/DB\nB4wbN64EShdCCFFW7Y3fTddvO7Jy/0pa+rZi8+BtEtjFoMgj7aSkJAICArTHXl5eJCYm4urqipeX\nFxkZGZw5cwY/Pz+ioqIICgrSnrt//36qVq2Kj4+P9rWFCxeSkpKCv78/YWFhODk53fSzK1Z0wWDQ\n321vxcbHx75P40h/ts3e+wP779Ge+ssz5zFn+xze+PMNzBYzL3d4mTdC3sCoN1q7tBJVWt/DO56I\npqqq9ntFUZgzZw5hYWG4ublRvfr1u66sXr2aQYMGaY+ffPJJGjRoQI0aNZg2bRqrVq1ixIgRN/2s\nlJTMOy2v2Pn4uJGYmGbtMkqM9Gfb7L0/sP8e7am/Y1eOMnHzaPYl7qVqhWos7LKEh1v2L+gv29rl\nlZji/h7e6geAIk+P+/r6kpSUpD1OSEi47sg5KCiIr776iqVLl+Lm5oafn582FhUVRYsWLbTH3bp1\no0aNGgB06dKF48eP31knQgghyhyzxcyH+xYR+l1H9iXu5ZH6Q9j6aCSd7wuxdml2p8jQ7tChAxs2\nbADg0KFD+Pr64urqqo0/++yzJCcnk5mZyZYtWwgODgYgPj6eChUq4ODgAOQfoT/99NNcu3YNyA/0\nevXqFXtDQgghSs/p1FMM+qEP0yNexc3Bjc96ruKD0I/xdKpo7dLsUpGnx1u2bElAQABDhgxBURSm\nTZvGmjVrcHNzo1u3bgwePJjhw4ejKAqjRo3Cy8sLgMTERO33kH8qffDgwTz99NM4OztTuXJlJk6c\nWHKdCSGEKDGqqrLi0HKmR7xGpimDvnUG8Hbnd6nkXMnapdk1Rf3nReoypixc57Gn6003Iv3ZNnvv\nD+y/R1vs73LGJSZuHsPW81vwcPRkTsd5PFjvERRF+ddzbbG/O1Wa17RlRTQhhBC37XDyIR776SEu\nZVyka41uvBuymCoVqlq7rHJDQlsIIcRt2XZ+K0+vf5y03GtMDX6DCc2fv+HRtSg5EtpCCCGK9N2x\nb5i0ZTwKCku7LWdQvYetXVK5JKEthBDiplRVZeGeBbwVNQMPR09W9PyK9n73W7uscktCWwghxA2Z\nLCZe2fYfVhxahp9rdb7u+z0NvRpZu6xyTUJbCCHEv2TkZTB64zNsjFtPgHdTvu67WiaclQES2kII\nIa6TmJnIsF8eYW/CHjpXD2F5zy9xc3C3dlkCCW0hhBD/cCn9IoN+6MOp1FiGNHyc+Z0X2v1mH7ak\nyGVMhRBClA+XMy7x4Lq+nEqNZWKLF3g/5EMJ7DJGjrSFEEIQn3GZB3/oS+zVkzzX4v94td00uQe7\nDJIjbSGEKOfiM+N58Ie+nLx6ggktJklgl2ES2kIIUY4lZCbw8A/9OHH1OOOaP8fUdjMksMswCW0h\nhCinEjMTeXhdP46lHGVMswlMC54pgV3GSWgLIUQ5lJSVxMPr+nH0yhFGB45jRvu3JLBtgIS2EEKU\nM8lZyTz0Qz+OXDnMyKZjeKPDbAlsGyGzx4UQopy4lH6RX07/xPIDH3Pi6nFGNB3Fm/fPlcC2IRLa\nQghhx2KvnuDnUz/xy6l17EnYrX19dOA4OcK2QRLaQghhR8wWMweT9vPL6R/55dRPHEs5CoBe0dPR\nrzO96/SlV+2+VHP1s3Kl4m5IaAshhA27kp3M7ss72R2/k13xu9gTv4v0vDQAnPRO9Kzdh961+9K9\nVk+8nLytXK24VxLaQghhQ5KzklkXu5Zdl6PZHb+TU6mx143X9axH6yr96VazJ11qhFLBWMFKlYqS\nIKEthBA24lpOKv3Wdufk1RMAuDt4EHJfV1pVbkPrKm1o4duKik5eVq6yfFBSrmCMjkJ/8gRMGg/o\nS+VzJbSFEMIGWFQL4zeP4uTVEzzR+BlGB46jbsV66BS5c7c06M6fw7gjAmPUDoxRERiOHikcbNoQ\nOnUvlToktIUQwgbM2zmHDWd+pXP1EN7utAC9rnSO7MoliwX9saMFIR2JMSoS/YXz2rDq4kJuxwfI\na9uOvPb34zmwNySll0ppEtpCCFHG/Xr6Z+btmkMN91os7b5cAru45eRg2Le3IKAjMEZHoUu9qg1b\nvL3J6d2PvLbB5LULxtQkEIz/2LK0FG+bk9AWQogy7ETKccZvGoWzwZnPe66SGeDFQLmWimFXNMYd\nkflH03t3o+TkaOPmmrXI7tm7IKTbY/avW6rBfCsS2kIIUUZdy0nlqV8fIz0vjaXdltOkUlNrl2ST\ndJcvFZ7q3hGJ/vBBFFUFQFUUTAFN84+g2waT1zYYS5WqVq745iS0hRCiDPrnxLNxzZ9jUL2HrV2S\nbVBV9CdPXB/SZ88UDjs5kRfcIf96dNtgTK2DUN09rFfvHbqt0J41axYxMTEoikJYWBiBgYHa2KZN\nm1iyZAkODg706dOHYcOGERUVxfPPP0+9evUAqF+/PlOnTuXSpUtMnjwZs9mMj48P77zzDg4ODiXT\nmRBC2LD5u+ay4cyvdKz+AK+1m27tcsquvDwM+/flz+reEYFx5w50ycnasMXTk5wevcgLKrgeHdgc\nHB2tWPC9KTK0o6OjiYuLIzw8nNjYWMLCwggPDwfAYrEwc+ZM1q5di6enJyNHjiQ0NBSAoKAgFi5c\neN17LVy4kKFDh9KrVy8WLFjA6tWrGTp0aAm0JYQQtmv96V94Z+dsarjV5JPun2HQyUnRvynpaRh2\n7cwP6OgdGHfvRMnK0sbN99Ug+4Guhdej6zcAnf3cFlfkn4TIyEgtiP39/UlNTSU9PR1XV1dSUlJw\nd3fHyyv/Zv527doRERGBn9+N17SNiopixowZAISEhLB8+XIJbSGE+IcTKccZt2kkzgZnPuslE8+U\n+HiM0ZEFM7t3YDi4H8VsBvKvR5sbNs4/1d2uff71aL/qVq64ZBUZ2klJSQQEBGiPvby8SExMxNXV\nFS8vLzIyMjhz5gx+fn5ERUURFBSEn58fJ0+eZMyYMaSmpjJhwgQ6dOhAVlaWdjrc29ubxMTEkutM\nCCFszLbzW3lhywTS89JYEvopTSsFFv0ie6Kq6E/HYtwRiSEqf2a34fSpwmEHB0yt2mi3XuW1aYvq\nWdGKBZe+Oz7nohbMuANQFIU5c+YQFhaGm5sb1avn/4RTq1YtJkyYQK9evTh37hxPPvkkGzduvOn7\n3EzFii4YDNa/H9HHx83aJZQo6c+22Xt/YP89mp0zeHHji3x14Ct0io43HniDMR1GWLusYnPT75/J\nBDExsG0bbN+e/ys+vnDc3R169oSOHaFjR5Q2bTA6OWG88btZVWn9GS0ytH19fUlKStIeJyQk4OPj\noz0OCgriq6++AmD+/Pn4+flRuXJlevfuDUCNGjWoVKkS8fHxuLi4kJ2djZOTE/Hx8fj6+t7ys1NS\nMu+qqeLk4+NGYmKatcsoMdKfbbP3/sC+ezRbzKw5+xWvbArjWm4qzX1a8E7n92jm28Juer7u+5eZ\niXHProJZ3REYdu1El1G4kpi5SlXyBj6YfyTdtj3mRo1B/48Dt7S8/F9lTHH/Gb3VDwBFhnaHDh1Y\ntGgRQ4YM4dChQ/j6+uLq6qqNP/vss8ydOxdnZ2e2bNnCM888w7p160hMTGTEiBEkJiaSnJxM5cqV\nad++PRs2bGDAgAFs3LiRjh07Fk+HQghhY2IS9jL5zxfYm7AHdwcP5nSaz1ONh9vVamdKcjL8tZkK\nG3/HGB2JIWYfismkjZvq1SenXXvygvKvSVtq1Cwzi5iUVUWGdsuWLQkICGDIkCEoisK0adNYs2YN\nbm5udOvWjcGDBzN8+HAURWHUqFF4eXnRpUsXXnrpJTZv3kxeXh7Tp0/HwcGBiRMnMmXKFMLDw6lW\nrRoDBw4sjR6FEKLMuJaTypzoN1l+8BMsqoXHmz7Oy62mU9mlsrVLuzeqiu5sXOGs7h0RGE4cB8AF\nUA0GTM2ak9c2f8JYXpu2qJUqWbdmG6Sot3Nx2UrKwukhez41B9KfrbP3/sD2e1RVlbhrZ4i8+BcR\nF7ez+exGkrKS8Pesy9xOC3ioRT/b7M9sRn/kcP5a3X8vYnL5kjZsqeCKqXUbHLqGcLVJS/JatgYX\nFysWXHLK1OlxIYQQt09VVU6nxhJRENKRF//iQnrhDlEVHSvyctBrjG/xPI56G1rkIzsb4749+UfQ\nUZEYd0aju5aqDVt8fMnpN1C7/crUuAkYDPj4uJFniz+UlFES2kIIcY/OXotj+4U/2XZ+K39d3Mbl\njMIjTm8nb/rU6U+HavcTXO1+Gnk3tok9sJWrKfmnuQtWGjPE7EXJzdXGTXX8yenTr/D+6Np15Hp0\nKZDQFkKIO3Q54xLbL/zJ9vN/sv3Cn5xNi9PGKjn7MMD/QYL9OtC+2v00qNgQxQbCTHfh/HX7RxuO\nHNbGVJ0OU9Nm+fdGB+VvqqEWcfePKBkS2kIIcZu+OPQZS2M+4MTV49rXPBw96V27Hx2rd+J+v87U\nr9ig7Ie0xYL++DHt1itjVCT68+e0YdXZmdwOHbWlQE2t26C62ve98rZCQlsIIW7DjkuR/GfrJJwN\nznSt0Y37/TrTsXonAryblv3btHJzMcTszd8/OjoSY/QOdCkp2rDFy4ucnn0KTnW3w9S0GchmTmWS\nhLYQQhQhIy+D538fC8C3/X4gqGpbK1d0a8q1VAy7orVZ3ca9u1Gys7Vxc42aZIf20K5Hm+vVl+vR\nNkJCWwghivDWjumcTj3FuObPlcnA1l2+lH8duiCkDYcPolgsQMGmGo2b5F+Pbpv/y1K1mpUrFndL\nQlsIIW7hrwvb+PTAUup51ufloNesXU7+phonT1x/PTruTOGwo6O2wlheu2BMrYNQ3T2sV68oVhLa\nQghxE+l56Tz/+zh0io5FXT/CyeBU+kXk5WE4EKPdemWMjkSXnKwNWzw8yeneM39Wd7v2mJo1B0cb\nuv9b3BEJbSGEuIk3IqZyNi2O51u+SMvKrUvnQ9PTMe7eqd16Zdy9EyWzcPMks191sh98OH850Hbt\nMTdoCLqyf9+3KB4S2kIIcQNbz23h80PLaOTVmJfavFxyH5SQgMPPvxWEdASGA/tRzGZt2NSwUcF6\n3QWbalS/r+RqEWWehLYQQvyPtNxrvLBlAnpFz6KuHxXfcqOqiu7M6cKj6B0REHuSv684q0Yjphat\ntPuj84Laolb0Kp7PFnZBQlsIIf7HtL9e5Xz6OV5sPYVAn+Z3/0ZmM4ZDBwpmdu/InzQWf1kbtri6\nQc+eZLRokx/ULVqBs3MxdCAH5oltAAAgAElEQVTslYS2EEL8w+9nf2PlkRUEeDflhVb/ubMXZ2Vh\n3LNLO4o27NqJLr1wswyzb2Wy+w/Kn9XdNhhT4yb4VPEkUzbUELdJQlsIIQqk5lzlhS0TMegMLOr6\nEQ76W68KplxJxhgdVRjS+/eh5OVp46a69chp96B2C5alZi1ZxETcEwltIYQAkrKSeHXbf7iUcZEp\nQa/SpFLT65+gqujOnS1cZSw6EsOxo4XDBgOmwGbarVd5Qe1QK1Uq5S6EvZPQFkKUS9mmbKIv72Dr\nuS1sPb+F/Yn7AGjm04LnWvxf/qYaRw5rs7qNUTvQX7ygvV51qUBupxBtVndey9ZQoYK12hHlhIS2\nEKLcOHblKL+f3cQf5zaz41IEWaYsABx0DnT17cijmXUZcNYHjycewxgdhe5aqvZaSyUfcvr015YD\nNTUJBIP8EypKl/yJE0KUC4v3vs8bkVO1x0FODXgiuy5dzjtQ5/AFHGOiUXK2aeOm2nXI7d1X2/nK\nXKeuXI8WViehLYSwez/FrmPZ+qmMSajI2MxA6h25jNOx4yjqMQBUnQ5Tk0DtVLcpqB2WylWsXLUQ\n/yahLYSwPxYL+hPHMe6IIH3rz4Rs38T5qwApwFZUJyfy2t+fH9Jt22Nq3QbVzd3KRQtRNAltIYTt\ny83FsH+fNqvbGBWJLiUFADcg2RnOdWxFxZCB+fdIBzYHh1vfziVEWSShLYSwOUraNQw7o/MDekck\nxj27ULKztXFzjZqkh3RhvkMU4V7nebT/TMa1fJ4sK9YsRHGQ0BZClHlKfHzBbVf5IW04dADFYgFA\nVRTMjQK0Wd15bYMxVa3KM+uH8evp8wxr9BRjWzxn5Q6EKB4S2kKIskVV0Z86mX8EHRUJO3dQKTa2\ncNjBAVObttqs7rw2bVE9PK97i7cip/Hr6Z+4368TczrNR5FZ38JOSGgLIazLZMJwcD/GHfkLmBij\nItElJRaOe3iQ3iWEz91PEFXLiF+nB+necBBNvJveMIy/PrKSRXvfxd+zLst7fFnkUqRC2BIJbSFE\n6crIwLh7Z+FyoLt3omRmaMPmqtXIHvRQwR7SwRjbNqbz513Ym3AenaLDsn8+c/fPp4Z7LXrX7kvv\nOv1oUzkIvU5PxIXtvLT1eTwdPVnV+1s8nSpasVEhip+EthCiRCmJiRijd+QfSUdHYtgfg2I2a+Om\nBg3z1+suuEfacl8NbRGTLFMWT4YPYG/CHoY0fJy37p/LlrOb+eX0j2w8s4GPYhbzUcxiKjn70LNW\nb34+tQ4Vlc96rqKOZ11rtSxEibmt0J41axYxMTEoikJYWBiBgYHa2KZNm1iyZAkODg706dOHYcOG\nAfD222+ze/duTCYTo0ePpnv37rz88sscOnQIT8/8608jRozggQceKP6uhBDWoarozpwuWK87/5fh\n5InCYYMBU/OW+RPG2rXPvx7t7X3Dt8o15zJi/RNsPbuVvnUGsOCBRRh0BvrXHUT/uoPIMeew/fxW\nfjn9E7+e/pmVR1YA8F7IB3Tw61gq7QpR2ooM7ejoaOLi4ggPDyc2NpawsDDCw8MBsFgszJw5k7Vr\n1+Lp6cnIkSMJDQ3lzJkznDhxgvDwcFJSUhg0aBDdu3cH4P/+7/8ICQkp2a6EEKXDbEZ/+JC2oYZx\nRwT6+MvasKWCK7kPdCkM6RatwMWl6Le1mBm/aRSbzm6kh38PloR+ikF3/T9XjnpHutbsTtea3Xm7\n07vsjI8mMy+DLjVCi71NIcqKIkM7MjKS0ND8vwT+/v6kpqaSnp6Oq6srKSkpuLu74+XlBUC7du2I\niIhgwIAB2tG4u7s7WVlZmP9xOkwIYaOysjDu3V24f/TOaHTpadqwxceXnH4DCzfVaNzkjjfVUFWV\n/2ydxA+xa2hbNZg1j64h4+qt//3Q6/S0qxp8Vy0JYUuK/NuUlJREQECA9tjLy4vExERcXV3x8vIi\nIyODM2fO4OfnR1RUFEFBQej1elwKfppevXo1nTp1Qq/XA7By5Uo+++wzvL29mTp1qhb4QoiyR0m5\ngjE6qjCkY/ai5OVp4yb/uuQMGJR/JB3UDkvtOve0qYaqqkyLeJWVR1YQ6NOcVb2/xcXoQgZpRb9Y\niHLgjieiqaqq/V5RFObMmUNYWBhubm5Ur179uudu2rSJ1atXs3z5cgAGDBiAp6cnjRo14uOPP2bx\n4sW8/vrrN/2sihVdMBj0d1pisfPxcbN2CSVK+rNtxdrf2bOwbRts357/30OHCsf0emjZEu6/X/tl\n8PXFADgX08e/sfUNPopZTKNKjdj01EZ8KvgA8j20dfbeH5Rej0WGtq+vL0lJSdrjhIQEfHx8tMdB\nQUF89dVXAMyfPx8/Pz8Atm3bxkcffcSnn36Km1t+M8HBhaevunTpwvTp02/52SkpmbffSQnx8XEj\nMdF+f8qX/mzbPfVnsaA/euS6SWP6C+e1YdXFhbyOD2izuvNatgZX1+vfoxj/334c8yHT/ppGDfda\nfNN7LWQ6kZiZJt9DG2fv/UHx93irHwCKDO0OHTqwaNEihgwZwqFDh/D19cX1H39xn332WebOnYuz\nszNbtmzhmWeeIS0tjbfffpvPP/9cmykOMHHiRCZPnsx9991HVFQU9erVu8fWhBC3LScHw769BQEd\ngTE6Cl3qVW3Y4u1NTu9+BZPGgjE1CQSjscTLyjPnMTt6Jov3vkdllyqs7vcDVV2rlfjnCmGLigzt\nli1bEhAQwJAhQ1AUhWnTprFmzRrc3Nzo1q0bgwcPZvjw4SiKwqhRo/Dy8tJmjU+aNEl7n7lz5/L4\n448zadIknJ2dcXFxYfbs2SXanBDlmZJ6FeOu6Py1uqMiMe7djZKTo42ba9Yiu2dvbb1uc91693Q9\n+m5cSr/IqN+eIepSJHU8/Pmi1zfU8qhdqjUIYUsU9Z8XqcuYsnBKxd5P7Uh/tu2f/ekuXSxYCjR/\npTH9kUMoBX+9VZ0OU0BT7VS3KagdlipVrVk6W85uZtymZ0nOTmaA/4MsCFmIm8O/97QuT99De2Tv\n/UEZOz0uhCiDVBX9ieOwdg9um7bkX48+G1c47OREXnCH/FuvgoIxtQlCdft3IFqD2WLmnV2zeXfX\nOxh1RuZ0ms8zAc/Kph5C3AYJbSFsQW4uhgMx2s5XxuhIdFeuAOAEWCpWJKdHr4L1utthatYCHMre\nRhnxmfGM/W0E2y/8SQ23mnzaYwXNfVtauywhbIaEthBlkJKehmHXzoL1unfkb6qRlaWNm++rQXZI\nKE7dunClcQvM9RuATmfFiov214VtjP5tOAmZ8fSs3YeFIR/Khh5C3CEJbSHKACUhoXBWd9QODAf3\nX7+pRqOAwluv2gZj8ctfE8HJxw2zDVwvXBrzAdMiXkWn6JjRfhZjmo2X0+FC3AUJbSFKm6qiPx2L\noWCtbmNUJIZTsYXDDg6YWrXRbr3Ka9MW1dM2j0gtqoXpEa/xUcxiKrtUYVmPLwmq2tbaZQlhsyS0\nhShpJhOGQwcKAnoHxqhIdIkJ2rDFzZ2crt0w/b2pRvOW4ORkxYKLR445h4mbR/Pfk2uoX7EBX/f9\nnvvcali7LCFsmoS2EMUtIwPjnl3arVfGXdEomRnasLlKVbIHPlgwaSwYc6PG+UuE2pHUnKs89etQ\nIi5up23VYL7o9TUVnWSfASHulYS2EPdISU7+x1KgERj2x6CYTNq4qX4DbVZ3Xrv2WO6rUeqLmJSm\nC2nneeznhzh65Qh96wzgw9BPcDLY/pkDIcoCCW0h7oSqojsbVzire0cEhhPHC4cNBkzNmmtH0XlB\n7VC9va1YcOk6nHyIx356iEsZFxnZdAxvdJiNXmdfZxGEsCYJbSFuxWxGf+RwwazugpXGLl/Shi0V\nXMntHKLN6s5r2RoKtqUtb/66sI2nfh3KtdxUpgW/ybjmE2WGuBDFTEJbiH/Kzsa4b0/+EXRUJMad\n0eiupWrDFh9fcvoNzD/V3TYYU0BTMMhfox9OrmH8plGoqCwJ/ZSH6g+2dklC2CX510aUa8rVFIw7\no7SVxgz79qDk5mrjpjr+5PTtr22qYaldx66vR9+NLw59xn+2TsLVwY3Pe66iY/XO1i5JCLsloS3K\nFd2F84WbakTtQH/08PWbajRtpq3Xndc2GNXX18oVl20f7F3IjMjX8Hby5tt+/6WpTzNrlySEXZPQ\nFvbLYoGDB3H6dZM2u1t//pw2rDo7k9eho3YUbWrdBtX15rvriEKqqjI3+k0W7H6HqhWqsbr/OupV\nrG/tsoSwexLawn7k5GCI2Ve4HGj0Drh6lb9j2OLlRU7PPgWTxtphCmwORqNVS7ZFFtXCa9un8OmB\npdRyr83q/uuo4V7T2mUJUS5IaAubpaRdw7AzqnARk727UbKztXFzjVrQrx9pzfOXBDXXqy/Xo++R\nyWLi//6YyDdHV9HQqxHf9fuByhWqWLssIcoNCW1hM3SXLxUEdASGqB0YDh9EsVgAUBUFc+Mm+dej\n/540VrUaPj5uZNvAhhq2IMecw9jfnuWnUz/QwrclX/f9Hi+n8nMPuhBlgYS2KJtUFX3syfxJYwUT\nx/RxZwqHHR3JCyrY9apdMKbWQajuHtar185l5mXyzPrH2XJuM+2r3c/K3uG4Osj1fyFKm4S2KBvy\n8jAciMnfUGNHBMboSHTJydqwxcOTnO4982d1t2uPqVlzcHS0YsHlg8liYlPcRt7d/TZ7E/bQrWYP\nPu3xBc4GZ2uXJkS5JKEtrCM9HePunYVrdu/eiZKZqQ2b/aqT/eDD+cuBtmuPuUFD0OmsWHD5cib1\nNF8d+ZKvj64kPvMyAA/VG8z7XT7EQe9g5eqEKL8ktEWpUBIS8tfq/ntTjQP7UcxmbdzUsNH1m2pU\nv8+K1ZZPOeYcfjn1IyuPfMG2838A4O7gwfAmIxnW+GmaVGpq3QKFEBLaogSoKrrTp/6x81UkhtiT\nhcNGI6aWrQuvSQe1Ra0o2zZaS3zGZRbve5/vjn3NlewrAARX68DjjZ6kn/9AORUuRBkioS3uncmE\n4fDBggljOzBERaJPiNeGLW7u5HYJLdxUo3lLcJYgsLZsUzYf7/+Qd3fPIyMvnUrOlRjX/DmGNXqK\nuhXrWbs8IcQNSGiLO5eZiXHvbm1Wt2FnNLqMdG3YXLkK2QMeLNhUoz3mxgGgl+0ZywpVVfn19M9M\niwgj7toZvJ28md7+TR5rOEyuVwtRxkloiyIpV5IxRkcVhvT+fSh5edq4qV59ctq1zz/d3TYYS81a\nsohJGXUk+TCv/fUy287/gUFnYHSz8bzUegoejp7WLk0IcRsktMX1VBXdubOFq4xFR2I4drRw2GDA\nFNhMu/UqL6gdaqVKVixY3I4r2cm8HT2Lzw8tw6Ja6FqjG290mC3rhQthYyS0yzuzGf2hg9q90cao\nHegvXtCGVZcK5HYKKVxprGVrqFDBigWLO5GZl8mKQ8t5d/fbXM25ir9nXWZ2mE1ozR7WLk0IcRck\ntMub7GyM+/ZgKFgOlF3ReKWmasOWSj7k9Omv3XplahIIBvljYmuyTdl8efgz3t+zgITMeNwc3JnR\nfhYjmo6S69ZC2LDb+td41qxZxMTEoCgKYWFhBAYGamObNm1iyZIlODg40KdPH4YNG3bT11y6dInJ\nkydjNpvx8fHhnXfewcFB/gEpSUrq1YL7o/NXGjPs24OSm1v4hLp1yerdD1PbYPLaBWOu7S/Xo21Y\njjmHVUe+4P3d87mUcREXQwUmtXyJsc0nUNFJbqsTwtYVGdrR0dHExcURHh5ObGwsYWFhhIeHA2Cx\nWJg5cyZr167F09OTkSNHEhoaytmzZ2/4moULFzJ06FB69erFggULWL16NUOHDi3xJssT3cUL2oQx\n445I9EcPo6gqAKpOh6lps4JZ3cHkBQVTqUld0mVDDZuXa87lm6OreHf3O1xIP4+LwYUJLSYxvvnz\neDvLph5C2IsiQzsyMpLQ0FAA/P39SU1NJT09HVdXV1JSUnB3d8fLK/8n+Hbt2hEREcG5c+du+Jqo\nqChmzJgBQEhICMuXL5fQvhcWC/oTxwtDOioS/bmz2rDq7Exe+/vzA7pde0yt26C6yiYP9mbtidW8\ntWMGZ9PicNI7MabZBCa0mISvi6+1SxNCFLMiQzspKYmAgADtsZeXF4mJibi6uuLl5UVGRgZnzpzB\nz8+PqKgogoKCbvqarKws7XS4t7c3iYmJJdCSHcvNxbB/nzar2xgViS4lRRu2eHmR07NPwUpjwZgC\nm4NcfrBbqqoy9fepvLntTRz1jowKHMvEFi/I/tZC2LE7nmGkFpxqBVAUhTlz5hAWFoabmxvVq1cv\n8jW3+tr/qljRBYPB+oty+PhY6ej02jWIjITt22HbNoiKguzswvFataBvX7j/fujYEV2DBjjqdNzp\n3ldW66+U2GN/JouJ0T+OZvm+5dSpWIf1j6+nnrf9rmJmj9/Df5L+bF9p9VhkaPv6+pKUlKQ9TkhI\nwMfHR3scFBTEV199BcD8+fPx8/MjJyfnhq9xcXEhOzsbJycn4uPj8fW99em7lJTMW46XBh8fNxJL\n6ZqvLv6yNqvbGLUDw6EDKBYLAKqiYG4UUHjrVdtgLNX8rn+D5Iw7/szS7M8a7LG/zLxMRm18mo1x\n62lVtRUreoTjafG1uz7/Zo/fw3+S/mxfcfd4qx8AigztDh06sGjRIoYMGcKhQ4fw9fXF1dVVG3/2\n2WeZO3cuzs7ObNmyhWeeeYaqVave8DXt27dnw4YNDBgwgI0bN9KxY8fi6dAWqSr62JMFE8byr0nr\nz5wuHHZ0JC+onTarO691EKqHrFpV3iVnJTPsl8Hsjt/JA/d1Yd3j/yX7mrWrEkKUliJDu2XLlgQE\nBDBkyBAURWHatGmsWbMGNzc3unXrxuDBgxk+fDiKojBq1Ci8vLzw8vL612sAJk6cyJQpUwgPD6da\ntWoMHDiwxBssM/LyMBzcn389Oir/mrTuH2cjLB6e5HTroc3qNjVvAU5OVixYlDVnr8Ux5KcHOXn1\nhLa3tZujG9nY91GMEKKQot7OxWUrKQunVO76tEd6OsY9u7RT3cbdO1EyC09fm6v5FZzqzt/5ytyw\nEeh0xVj57bH3U1dlvb8jyYf5ZP8S6njWpWmlQJr6BOLl9O9btA4mHeCxnx4iPvMy45s/z9TgGegU\nXZnvrzjYe4/Sn+0rU6fHxe1REhPzFzEpWA7UsD8GxWzWxk0NGxWs111wPfq+GlasVpQFV7NTeOKX\nRzmbFnfd1/1cq9O0UiBNKgXS1KcZqqoy8fcxpOVeY2aH2YxuNt5KFQshrE1C+26oKrozp7V7o41R\nkRhOnigcNhoxtWil3R+d1yYI1UsWuBCFLKqFCZtHczYtjnHNn6NV5dYcSNzPgaQYDiTtZ/2ZX1h/\n5hft+UadkaXdljOo3sNWrFoIYW0S2rfDbMZw+GDBzO6CRUziL2vDFlc3ckO6arO681q0AhcXKxYs\nyrrFe99jY9x6OlcPYWq7Geh1evr5F87xiM+M52BifoDHXTvD4AaPEVytgxUrFkKUBRLaN5KVhXHv\nboxRkbAnGu+/ItClF16vMPtWJrv/IEx/b6rRKEA21RC37a8L25gV9QZVK1RjSbdl6HX/Xougsktl\nKtfsTtea3a1QoRCirJKkAZSUKxijo7Tbrwwxe1Hy8rRxi39dcgYMKpjZ3Q5L7TqyqYa4K/EZlxm1\n8Rl0io5Puq+gkrPsRS6EuH3lL7RVFd35c4WzuqMjMRw9Ujis12MKbFYwaaw9Hr1DSVGcrViwsBcm\ni4lRvz1DYlYCMzvMJqhqW2uXJISwMeUntC0WXMP+g8P6X9BfvKB9WXVxIbfjA9r+0XktW8M/Fo/B\nxw3s/HYFUTpmRb1B5MW/6FtnAKMCx1m7HCGEDSo/oZ2VheMPa0BRyOnTX9ue0tQkEIxGa1cn7Nyv\np39m8d73qOPhz/tdPkCRyytCiLtQfkK7QgWSD57MX8BE/sEUpehM6mkmbh6Ds8GZ5T1X4ubgbu2S\nhBA2qvyENoDe+juGifIl25TNiA1Pci03lYVdltDYO6DoFwkhxE2U/rqZQpQTmXmZTNg8mgNJMQxr\n9BRDGj5u7ZKEEDaufB1pC1FKTl09yfANT3I4+SCtKrfhrY5vW7skIYQdkCNtIYrZT7Hr6Lb6AQ4n\nH+SpgBGsHfAzzga5bVAIce/kSFuIYpJnzuPNHdNZErMIF4MLi7suZXCDx6xdlhDCjkhoC1EMLmdc\nYuTGp4m6FEldz3os6/EljbwbW7ssIYSdkdAW4h5tv/AnozY+Q1JWIv39B/FeyGJcHW6+H64QQtwt\nCW0h7pLZYmbhngXM3fkWOkXHmx3mMDJwrCycIoQoMRLaQtyF2KsnmLh5LLvio6lWwY9PenxOmyqy\nlrgQomRJaAtxByyqhU/2L+GtHTPINmczsO6DzO44H29nb2uXJoQoByS0hbhNp1NP8fzv49hxKQJv\nJ28Wd11K/7qDrF2WEKIckdAWoggW1cJnBz9lZuTrZJoy6VOnP293ehcfFx9rlyaEKGcktIW4hbPX\n4pi0ZTzbL/yJp6MnC0IWMajuwzLZTAhhFRLaQtzEH+d+55n1w8jIS6dHrV7M6/w+lStUsXZZQohy\nTEJbiBuIvPgXT/36GBbVwsIuS3i0wVA5uhZCWJ2EthD/Y3f8Tob+/Agmi4nPe66iW62e1i5JCCEA\nCW0hrnMgMYYhPz1ElimTT7qvkMAWQpQpEtpCFDh65QiDfxzItZxUFnddSj//AdYuSQghriOhLQT5\n+18/vK4/ydnJzH9gIY80GGLtkoQQ4l9uK7RnzZpFTEwMiqIQFhZGYGCgNrZq1SrWrVuHTqejSZMm\nvPrqqyxZsoSIiAgALBYLSUlJbNiwgS5dulClShX0ej0A8+bNo3LlyiXQlhC37+y1OB5a15+EzHje\nun8uTzR+2tolCSHEDRUZ2tHR0cTFxREeHk5sbCxhYWGEh4cDkJ6ezrJly9i4cSMGg4Hhw4ezb98+\nxo4dy9ixYwFYu3YtycnJ2vt98sknVKhQoYTaEaLQgcQYLl8+S0UqU8ujDt5O3v+aAX4p/SIPrevH\nhfTzvNZuBiMDx1qpWiGEKFqRoR0ZGUloaCgA/v7+pKamkp6ejqurK0ajEaPRSGZmJi4uLmRlZeHh\n4aG91mQy8fXXX/PFF1+UXAdC3MB3x77hud/HYlbN2tcqGF2p5V6bmu61qOVRmxruNVm2fylx187w\nYuspPNfyBStWLIQQRSsytJOSkggICNAee3l5kZiYiKurK46OjowfP57Q0FAcHR3p06cPtWvX1p67\nceNG7r//fpycnLSvTZs2jQsXLtCqVStefPHFW977WrGiCwaD/m57KzY+Pva9N7K99ffx7o+ZsHkM\nHk4ehN0fxuX0y8SmxHIq5RSxKbEcSj5w3fNfCn6Jt7vNttn7sO3t+3cj9t6j9Gf7SqvHO56Ipqqq\n9vv09HSWLl3K+vXrcXV15amnnuLo0aM0bNgQgO+//54ZM2Zoz3/uuefo2LEjHh4ejB8/ng0bNtCz\n581vqUlJybzT8oqdj48biYlp1i6jxNhbfx/FLOb1v8Ko5FyJ8H7/pUujDtf1p6oqiVmJxF07zZnU\n01QwutKrdh+SktKtWPXds7fv343Ye4/Sn+0r7h5v9QNAkaHt6+tLUlKS9jghIQEfn/yNEmJjY7nv\nvvvw8vICoHXr1hw8eJCGDRuSmZnJ5cuXqV69uvbagQMHar/v1KkTx48fv2VoC3G7VFVlwe63mRv9\nFlUqVGV1v3XU92rwr+cpioKviy++Lr6y/7UQwuboinpChw4d2LBhAwCHDh3C19cXV1dXAPz8/IiN\njSU7OxuAgwcPUqtWLQCOHj1KnTp1tPdJS0tjxIgR5ObmArBz507q1atXrM2I8klVVWbumMbc6Leo\n4VaTdQPX3zCwhRDC1hV5pN2yZUsCAgIYMmQIiqIwbdo01qxZg5ubG926dWPEiBE8+eST6PV6WrRo\nQevWrQFITEzUjsAB3Nzc6NSpE48++iiOjo40btxYjrLFPbOoFl7Z9hKfHfwUf8+6fN//R6q5+lm7\nLCGEKBGK+s+L1GVMWbgOYu/XY2y5P5PFxAtbJhB+7Csaezfh237/xdfF97rn2HJ/t8Pe+wP771H6\ns31l6pq2EGVRel46k34fz7rYtbTwbck3fddQ0cmr6BcKIYQNk9AWNuf3s5v4z9ZJnEs7S7uq7VnV\n51vcHNytXZYQQpQ4CW1hM65kJzN1+yt8d/wb9Iqe51u+yIutp+BkcCr6xUIIYQcktEWZp6oqP5xc\nQ9j2/5CUlUSgT3PeDVlM00qBRb9YCCHsiIS2KNMupl9gyp//x4Yzv+Kkd+L14JmMaTYeg07+6Aoh\nyh/5l0+USRbVwpeHP2dGxFTS89LoUK0j80MWUsfD39qlCSGE1UhoizInMy+TCZtH89OpH3B38GD+\nAwsZ1ugpm10bXAghiouEtihT4jMu8+SvQ9ibsIf21e7no27LqFKhqrXLEkKIMkFCW5QZh5IOMuyX\nwVxIP8+jDYYy/4GFOOgdrF2WEEKUGRLaokzYFLeBkRufISMvnVfbTuO5lv8np8OFEOJ/SGgLq1t2\nYCmvbp+Cg86BT7uvoH/dQdYuSQghyiQJbWE1ZouZqX+9zKcHllLJ2Ycve39Dq8ptrF2WEEKUWRLa\nwirSc9MY/dtwfovbQEOvRqzs/S013GtauywhhCjTJLRFqbuSncyjPz5ITOJeHrivC592X4G7o4e1\nyxJCiDJPZ+0CRPmSkJnAoP/2JSZxL0MbPsFXfVZLYAshxG2S0Bal5lL6RQb9tzdHrhxieJORLAhZ\nJMuRCiHEHZDQFqXiXNpZBvy3FyeuHmdc8+eY3XEeOkX++AkhxJ2QwxxR4k6nnuKhH/pxPv0c/9d6\nMlPavCr3YAshxF2Q0BYl6kTKcR5a14/LGZcIa/s6k1q9ZO2ShBDCZkloixJzOPkQD6/rT1JWIm90\nmMWYZhOsXZIQQtg0CSjUPrMAABa7SURBVG1RIvYn7uORdQNIyUlhbqcFPNPkWWuXJIQQNk9CWxS7\nXZejGfLTQ6TlXuO9kA8Y2ugJa5ckhBB2QUJbFKvtF/5k2M+PkmPO5sPQT3io/mBrlySEEHZDQlsU\nm01xGxi+/gksqoVlPb6kd52+1i5JCCHsioS2KBY/xv7AmN+GY9AZ+KLXN3SpEWrtkoQQwu7I6hbi\nnn177GtGbnwKB70j3/RdI4EthBAlREJb3JPPDy5jwubRuDm4833/dQRX62DtkoQQwm5JaIu7tmTf\nYib/+QKVnCuxdsDPtKzc2tolCSGEXbuta9qzZs0iJiYGRVEICwsjMDBQG1u1ahXr1q1Dp9PRpEkT\nXn31VdasWcP7779PjRo1AGjfvj1jx47l6NGjTJ8+HYAGDRowY8aM4u9IlDiLamHBrrd5e+csqlao\nxur+66hXsb61yxJCCLtXZGhHR0cTFxdHeHg4sbGxhIWFER4eDkB6ejrLli1j48aNGAwGhg8fzr59\n+wDo3bs3U6ZMue693nrrLS30X3zxRbZu3Urnzp1LoC1REi6mX+Cbo6v4+uhK4q6doYZ7Lb7vv46a\n7rWsXZoQQpQLRYZ2ZGQkoaH5E4v8/f1JTU0lPT0dV1dXjEYjRqORzMxMXFxcyMrKwsPjxnsj5+bm\ncuHCBe0oPSQk5P/bu/+4qOp8j+Ov4dcIDiCDQAjiD1bBJFlaalMKRcE0XatH3dJWkcR+rGht7QqK\nJXX3mr/IyjRF1JsZpitSy5YJ19DyJuGPJbuDkco+SjJBEE1HUJnhe/9wndUUFNQZZvg8H48eOQzn\n8Hn79ZzPnO85nENxcbE07XbuvPk8Bd9vZt23a9lW+RlNqgkPFw8eD3uC9N/OJlDXzdYlCiFEh3HN\npl1bW0v//v0tr/V6PTU1Neh0OrRaLSkpKcTHx6PVahk1ahS9evWitLSUXbt2kZycjMlkIi0tDV9f\nX7y8vCzr8fX1paampsWf7ePjgYuL8w3Euzn8/DxtXcJNpZRCoQAwN5nR+3pYXit14f/fHf+O1aWr\nWfvNWmrrawH4bdBvSY5K5vGIx/HSel195e2Qo43fLzl6PnD8jJLP/lkrY6t/T/viTh0uTI9nZWWx\nZcsWdDodEydOpLy8nMjISPR6PUOGDKG0tJS0tDRWrlzZ7Hqac+JEfWvLu+n8/DypqTlt6zJumnPm\nc0zY/DjbK4uu6/t9O/nybORUnug3gXB9vwvrOAU12MffiaON3y85ej5w/IySz/7d7IwtfQC4ZtP2\n9/entrbW8vrYsWP4+fkBUFFRQffu3dHr9QBER0djMBh49NFHCQ0NBSAqKoq6ujp8fHw4efKkZT3V\n1dX4+/u3LZFos4wv09leWUSYTzh+Hv64ujpjamy68Oa/nnGtQYO31puHf/Uow3uOwM3ZzYYVCyGE\nuOiaTTsmJoa3336bsWPHUlZWhr+/PzqdDoCgoCAqKio4e/YsnTp1wmAwMHjwYLKzswkMDGT06NEc\nOHAAvV6Pm5sbvXv3Zs+ePURHR1NYWMiECfIgCWv66OAmVhuy6ae/nU8fKcLD1aNDfAoWQghHcc2m\nfeedd9K/f3/Gjh2LRqMhIyODvLw8PD09SUhIIDk5mcTERJydnYmKiiI6Oprg4GCmT5/O+vXrMZlM\nzJkzB4D09HRmz55NU1MTkZGRDBo06JYHFBdUnDzIi9ufw8OlMyvvfw8PVw9blySEEKKVNOp6Ti7b\nSHs4AnSEI9EGUwMjNw1j/3EDy+JXXvbkLUfI1xLJZ/8cPaPks3/WPKctd0TrAGbtSGX/cQMT+yfL\nozKFEMKOSdN2cBvK1/H+t2u4o2skf4mZa+tyhBBC3ABp2g6svO5b0r54EU83L1bev4ZOLp1sXZIQ\nQogbIM/TdlDGRiOTCxKpN9Wz+v736eXd29YlCSGEuEFypO2AlFKkfv4CB058xzMDpjA6dIytSxJC\nCHETSNN2QDnfvkfugQ38JiCalwf+p63LEUIIcZPI9LgDKa3eyyrDCj48mEsXbRdWDH9X7mYmhBAO\nRJq2nTtnPkf+oQ9ZbVjB3uo9APyqSx8WDn6T7p4hNq5OCCHEzSRN2079ZDzCe2WreW//u9Q21KBB\nw4ieDzDpjqeJDR6Ck0bOfAghhKORpm1H6s4eZ8ePn5Nf8RGb//l3zMpMF20XUn79PEkRyfTw6mnr\nEoUQQtxC0rTbsUZzI3uqd7G98jO2Vxbx9bFSy3Ov+/veweQ7nuHhPo/KfcSFEKKDkKbdztQ21PK3\nQ3l8XlnEjiNfcKbRCICLkwv3dBtEXPdhxHUfxgC/X6P516M0hRBCdAzStNuRvdW7mfjpExyrrwag\nt3cocSFPMKT7MGK63YvOrfmbyAshhHB80rTbiU0H/soft6XQ2NRI6l3p/EfYWDlHLYQQ4jLStG2s\nSTUxf9d/8cbeTDzdvHh3RA7Degy3dVlCCCHaIWnaNnSm8QxTP3uGT/6ZTw+vnuQ8sJG++jBblyWE\nEKKdkqZtI0dO/8iET8diqP2GmG73sWrEe+g7+dq6LCGEEO2Y3IHDBvZW72Z47hAMtd8w4fYkNvzu\nQ2nYQgghrkmOtK0s7+BGni+aQmNTI3Punc/kO56VX90SQghxXaRpW9H2yiKmbH2Kzq461oxcx9CQ\nBFuXJIQQwo5I07aSytOHefZ/JuGiceGvv/uQ3wTcZeuShBBC2Blp2lZw1nSWSVsmUHe2jszBb0nD\nFkII0SZyIdotppRixhd/Yl9NKePCxzPh9iRblySEEMJOSdO+xd7/dg3rytcywO/XzIt9XS46E0II\n0WbStG+hf1TvYeYXf8ZH68Pq+9fi7uJu65KEEELYMWnat0htQy3JBYk0NjWyPGE1IV49bF2SEEII\nOydN+xYwNZl4pvBJjhh/ZMbdLxEXMszWJQkhhHAA13X1+Guvvca+ffvQaDSkp6czYMAAy3s5OTnk\n5+fj5OREREQEs2bNwmQyMWvWLA4fPozZbCY1NZXo6GgmTJhAfX09Hh4eAKSlpREREXFrktnQ3JK/\nsOPI54zo+QDP/+ZPti5HCCGEg7hm0961axc//PADGzZsoKKigvT0dDZs2ACA0Whk1apVFBYW4uLi\nwqRJk/j666+pqKjA3d2dDz74gIMHDzJz5kxyc3MBmDt3Ln379r21qWzo44p83i59g17evVkyLAsn\njUxmCCGEuDmu2bSLi4uJj48HIDQ0lJ9//hmj0YhOp8PV1RVXV1fL0XNDQwPe3t6MGTOG0aNHA6DX\n6zl58uStTWFF58znqD5TRdWZKqrrq6g+c5SqM1VU1R+l+kwVu6tK8HDx4N0R6/DSetu6XCGEEA7k\nmk27traW/v37W17r9XpqamrQ6XRotVpSUlKIj49Hq9UyatQoevXqddnya9assTRwgMWLF3PixAlC\nQ0NJT0+nU6dONzHOraOUYs5Xr7Lk6zdpUk3Nfl9Xdz8WxL5BP9/brVidEEKIjqDVd0RTSln+bDQa\nycrKYsuWLeh0OiZOnEh5eTnh4eHAhfPdZWVlLF++HIDExETCwsIICQkhIyODnJwckpOTm/1ZPj4e\nuLg4t7bEm65rVx3pn6WzuHQRPbx7ENsjlkBdIN08u1n+C/QMJFAXiLur/f1al5+fp61LuKUkn/1z\n9IySz/5ZK+M1m7a/vz+1tbWW18eOHcPPzw+AiooKunfvjl6vByA6OhqDwUB4eDgbN26kqKiId955\nB1dXVwASEv79gIyhQ4eyefPmFn/2iRP1rU90k/n5eZK6OZ3MPfPo7R3K3x76lIDOt135jSYwnjRh\n5LT1i7wBfn6e1NTYV82tIfnsn6NnlHz272ZnbOkDwDWvkoqJiaGgoACAsrIy/P390el0AAQFBVFR\nUcHZs2cBMBgM9OzZk8rKStavX8+SJUvQarXAhSP0pKQkTp06BUBJSQl9+vS5sWRWMHfHXDL3zKOH\nV0/yHvz46g1bCCGEsIJrHmnfeeed9O/fn7Fjx6LRaMjIyCAvLw9PT08SEhJITk4mMTERZ2dnoqKi\niI6OZtGiRZw8eZKnn37asp5Vq1bx2GOPkZSUhLu7OwEBAUybNu2WhrtRy75eQsbOdIJ13cl78GO6\n6YJsXZIQQogOTKMuPUndzthySmXV/2Uxc8d0gjyDyBvzCb28e9usllvJ0aeuJJ/9c/SMks/+WXN6\nXB7NeRXvlf03M3dMx8/dn88SP0Ovutm6JCGEEEJuY/pL68tzmP75H/Ht5MumB/9OWNcwW5ckhBBC\nANK0L/PX7z7gj9tS8NZ6s3FMPuH6frYuSQghhLCQ6XHAeP40L/3vDNaVr8XLzZuNv/sbEV3vsHVZ\nQgghxGU6fNPeXVXClK1P8cOp74noOoBl8SsJ04fbuiwhhBDiCh22aTeaG1m0dwFv7F2IUoppUS+Q\ndvcs3JzdbF2aEEIIcVUdsmlXnDzIlK1PUXrsHwTrurM0fgUDu8XYuiwhhBCiRR2qaSulWLv/XWZ/\nOZN6Uz2P9n2cefdlytO4hBBC2IUO07SbVBNPFSbx94qP8NZ2YUXcUh7q84ityxJCCCGuW4dp2g2m\nBnb8uJ3Y4DgWD31HbkkqhBDC7nSYpt3ZtTP7n/wnLk4dJrIQQggH06FuriINWwghhD3rUE1bCCGE\nsGfStIUQQgg7IU1bCCGEsBPStIUQQgg7IU1bCCGEsBPStIUQQgg7IU1bCCGEsBPStIUQQgg7IU1b\nCCGEsBPStIUQQgg7IU1bCCGEsBMapZSydRFCCCGEuDY50hZCCCHshDRtIYQQwk5I0xZCCCHshDRt\nIYQQwk5I0xZCCCHshDRtIYQQwk642LoAa3vttdfYt28fGo2G9PR0BgwYYHkvJyeH/Px8nJyciIiI\nYNasWZhMJmbNmsXhw4cxm82kpqYSHR3NhAkTqK+vx8PDA4C0tDQiIiJsFesyrc2Yl5fHW2+9RUhI\nCACDBg3iD3/4A+Xl5bzyyisAhIWF8eqrr9oizhVam2/ZsmXs3LkTgKamJmpraykoKGDo0KHcdttt\nODs7A5CZmUlAQIBNMl2qpXxbt25l2bJluLm5MWrUKMaPH9/sMkePHiU1NRWz2Yyfnx8LFy7Ezc3N\nVrEs2pJvwYIF7N27F5PJxDPPPMPw4cOZMWMGZWVldOnSBYDk5GSGDBlii0hXaG3GkpISnn/+efr0\n6QNA3759efnllx1mDDdu3Eh+fr7lewwGA6Wlpe16P3rgwAGmTJlCUlKS5d/hRTt37mTRokU4OzsT\nGxtLSkoKYKXtUHUgJSUl6umnn1ZKKXXo0CH12GOPWd47ffq0iouLU42NjUoppZ588klVWlqqcnNz\nVUZGhlJKqQMHDqhHHnlEKaXU+PHj1XfffWfdANehLRk3bdqk5s2bd8W6xo8fr/bt26eUUurFF19U\n27dvt0KClrUl36Xy8vJUdna2UkqpuLg4ZTQarVT59Wkpn9lsVrGxser48ePKbDarSZMmqaNHjza7\nzIwZM9TmzZuVUkq9/vrrKicnx8pprtSWfMXFxWry5MlKKaXq6urU4MGDlVJKpaWlqaKiIqtnuJa2\nZPzqq6/UtGnTrliXo4zhL5d/5ZVXlFLtdz965swZNX78ePXSSy+ptWvXXvH+yJEj1U8//aTMZrMa\nN26cOnjwoNW2ww41PV5cXEx8fDwAoaGh/PzzzxiNRgBcXV1xdXWlvr4ek8lEQ0MD3t7ejBkzhpkz\nZwKg1+s5efKkzeq/Hm3JeDXnz5/nyJEjlk/QcXFxFBcXWydEC24kn8lk4oMPPrjiU3N70lK+EydO\n4OXlhV6vx8nJiXvuuYedO3c2u0xJSQnDhg0D7GP8mst311138dZbbwHg5eVFQ0MDZrPZZhmupS0Z\nm+MoY3ippUuXMmXKFKvX3Rpubm5kZ2fj7+9/xXuVlZV4e3sTGBiIk5MTgwcPpri42GrbYYdq2rW1\ntfj4+Fhe6/V6ampqANBqtaSkpBAfH09cXByRkZH06tULV1dXtFotAGvWrGH06NGW5RcvXszvf/97\nZs+ezdmzZ60bphltyQiwa9cukpOTmThxIvv377dsfBf5+vpa1mNLbc0HUFhYyL333kunTp0sX8vI\nyGDcuHFkZmai2sHNAVvKp9frOXPmDN9//z2NjY2UlJRQW1vb7DINDQ2WaTh7GL/m8jk7O1umT3Nz\nc4mNjbWc0nj//fdJTEzkhRdeoK6uzvqBrqItGQEOHTrEs88+y7hx4/jyyy8BHGYML/rmm28IDAzE\nz8/P8rX2uB91cXG5bD9xqZqaGvR6veX1xfzW2g473DntS126kzYajWRlZbFlyxZ0Oh0TJ06kvLyc\n8PBw4MK50rKyMpYvXw5AYmIiYWFhhISEkJGRQU5ODsnJyTbJ0ZLryRgZGYler2fIkCGUlpaSlpbG\nypUrm11Pe9KaMdy0adNl5+Wfe+457rvvPry9vUlJSaGgoIARI0ZYPUNLLs2n0WiYN28e6enpeHp6\nEhwcfM1lWvpae9CafFu3biU3N5fVq1cD8OCDD9KlSxf69evHihUrWLJkCbNnz7Zq/dfjejL27NmT\nqVOnMnLkSCorK0lMTKSwsLDZ9bQnrRnD3NxcHn74Yctre9mPtsWt2g471JG2v7//ZZ/6jh07ZvnE\nV1FRQffu3dHr9bi5uREdHY3BYABg48aNFBUV8c477+Dq6gpAQkKC5cKtoUOHcuDAASunubq2ZAwN\nDbVcwBMVFUVdXR0+Pj6XnQqorq6+6lSRtbV1DOvr66mqqrpsJ/LQQw/h6+uLi4sLsbGx7WIMW8oH\ncPfdd7Nu3TqysrLw9PQkKCio2WU8PDwsRy72MH5w9XwAO3bsYPny5WRnZ+Pp6QnAwIED6devH2A/\n2yBcPWNAQAAPPPAAGo2GkJAQunbtSnV1tUONIVyY7o+KirK8bq/70Zb8Mv/FcbHWdtihmnZMTAwF\nBQUAlJWV4e/vj06nAyAoKIiKigrLX67BYKBnz55UVlayfv16lixZYpkmV0qRlJTEqVOngAv/EC9e\n9WlrbcmYnZ3Nxx9/DFy4YvJi0+vduzd79uwBLkwt33fffTZIdLm25AMoLy+nd+/elvWcPn2a5ORk\nzp8/D8Du3bvbxRi2lA9g8uTJHD9+nPr6erZt28bAgQObXWbQoEGWr9vD+MHV850+fZoFCxaQlZVl\nuVIcYNq0aVRWVgL2sw3C1TPm5+ezatUq4ML06/HjxwkICHCYMYQLDatz586WqeL2vB9tSXBwMEaj\nkR9//BGTycS2bduIiYmx2nbY4Z7ylZmZyZ49e9BoNGRkZLB//348PT1JSEhg/fr15OXl4ezsTFRU\nFKmpqSxatIhPPvmEbt26WdaxatUqtm7dysqVK3F3dycgIIA5c+bg7u5uw2T/1tqMVVVVTJ8+HaUU\nJpPJ8qsKhw4dYvbs2TQ1NREZGWm5IM/WWpsPoKCggJ07d142Pb5mzRo++ugjtFott99+Oy+//DIa\njcZWsSxayldYWMjSpUvRaDRMmjSJMWPGXHWZ8PBwjh07RlpaGufOnaNbt27MnTvXMlNkS63Nt2HD\nBt5+++3Lrk+YP38+hw8fZuHChbi7u+Ph4cHcuXPx9fW1YbJ/a21Go9HIn//8Z06dOkVjYyNTp05l\n8ODBDjOGcOFD9JtvvnnZqbfNmze3y/2owWBg/vz5HDlyBBcXFwICAhg6dCjBwcEkJCSwe/duMjMz\nARg+fLhlSt8a22GHa9pCCCGEvepQ0+NCCCGEPZOmLYQQQtgJadpCCCGEnZCmLYQQQtgJadpCCCGE\nnZCmLYQQQtgJadpCCCGEnZCmLYQQQtiJ/weJ44Jbe5SDmQAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " # YOUR CODE HERE\n",
+ " x = tf.placeholder(tf.float32, name='x')\n",
+ " y = tf.placeholder(tf.float32, name='y')\n",
+ " W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ " b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ " pred_y = (W*x) + b\n",
+ " loss = tf.reduce_mean(tf.square(y - pred_y))\n",
+ " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n",
+ " with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()\n",
+ " pass"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 551
+ },
+ "outputId": "c3403cde-4a2b-472f-b4e3-8b70b39e5442"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500)"
+ ],
+ "execution_count": 30,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.23320778\n",
+ "Loss after epoch 50 is 0.23203653\n",
+ "Loss after epoch 100 is 0.23087405\n",
+ "Loss after epoch 150 is 0.22972041\n",
+ "Loss after epoch 200 is 0.22857524\n",
+ "Loss after epoch 250 is 0.22743858\n",
+ "Loss after epoch 300 is 0.22631061\n",
+ "Loss after epoch 350 is 0.22519088\n",
+ "Loss after epoch 400 is 0.22407953\n",
+ "Loss after epoch 450 is 0.22297664\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.023238085\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3XdAVfX/x/HnZYMsLwLuhVvTNLfl\nCis1q2/5M/1mZmrmapsDc5Q5Uxu2zOxb33J9Mytbapa2xD3R1MScqEyRDRfO7w/0JorgAO7l8nr8\ng/eecd9vrvDi8znnnmMyDMNARERE7IaTrQsQERGRvBTOIiIidkbhLCIiYmcUziIiInZG4SwiImJn\nFM4iIiJ2xsXWBVwUE5Nk09cvX96LhIRUm9ZQnBy9P3D8HtVf6ebo/YHj91jU/QUG+lx1mUbOF7i4\nONu6hGLl6P2B4/eo/ko3R+8PHL/HkuxP4SwiImJnFM4iIiJ2RuEsIiJiZxTOIiIidkbhLCIiYmcU\nziIiInZG4SwiImJn7OYiJPZo/vzXOXjwT+Lj40hPT6dy5Sr4+voxffprRbL/3r17ERQUjJPTP38j\nvf32Bze9399//4U2bdpz/nwiixYtYMyYCTe9TxERKTnXFM6HDh1ixIgRDBw4kP79++dZtnHjRubN\nm4ezszMdO3Zk5MiRAEyfPp3du3djMpkICwujadOmRV99MXvqqecA+P77bzhyJJJRo54t8teYM+ct\nvLy8inSfy5YtpkWLVgQEVFAwi4iUQoWGc2pqKlOnTqVdu3b5Ln/11VdZtGgRwcHB9O/fn7vvvpv4\n+HiOHTvG8uXLiYyMJCwsjOXLlxd58bayY8c2li37jNTUVEaNeo4XXhjFd9/9BMBLL43hwQf70KBB\nQ6ZPf5mkpCSys7N59tkXqVOn7jXtv2fPO6/Y386d20lJSeb48WOcOnWSp59+gXbtOrB69XesWLEc\nk8lE376PkJWVxf79EYwe/TTjxk3k5ZdfYtGiT9m8eTOzZ8/BxcWFwMAgxo+fxLp1a9izZxfnziVw\n/Pgx/v3vR7n33geK7fsmIiLXptBwdnNzY+HChSxcuPCKZSdOnMDPz49KlSoB0KlTJ8LDw4mPjyc0\nNBSAkJAQEhMTSU5Oxtvb+4YLnbLxJb6J/OqGt89Pr5AHmNL+1RvaNjLyMEuXrsTNzS3f5f/731La\ntGlPr14P8PffR3jzzTm88ca7N1Mu0dFnmTPnLTZt2sjXX39Bs2a38vHHH/LJJ0vJzMxi2rTJzJw5\njw8/fJ85c94iMfGcddvJkyczZ858goMrMm/eLH78cTUmk4nIyMO8//5HnDx5gsmTwxTOIiL5+Pn4\nOupaalDN5doGWTer0HB2cXHBxSX/1WJiYjCbzdbHZrOZEydOkJCQQOPGjfM8HxMTU2A4ly/vVeB1\nS7083XByMhVW7nXx8nTLc+Hxq12E3MfHAy+vf9b19/eiUaOGVKkSAIDJZLIuc3d3xd/fi4MH9xEf\nH8/69WsByMhIu2L/zs5OjB//HM7OuX2XL1+et956K9/9lSvnTrt2bQgM9KF+/VpkZKSRmBhN3bp1\nqFo1EIBFixZa91uhgjfOzlm4uDjh6pqNyWSiSZPc/1SdO9/B1q1badSoEa1a3UbFiv74+LiSlpZS\n4IXYS4PSXn9h1F/p5uj9geP1mJieyIjvR7Bk7xLurXcv3/T7pkRet0ROCDMMo9B1CrvTx5jmkxjT\nfFJRlWR18W5YgYE+V70zVlJSOqmpmdbl586lYhgm62PDMKz/TklJsy5/6qkXaNLkn2Ptl+8/OzuH\nGTNez3PMOSYmKd/9paRk4OrqSUxMEgkJKWRmWkhMTCc9PTPf/cbGJpOYmILFkkNcXEqefcbFnSc9\n3UJSUjqZmTnExCSRmppKdnaOze8OdjMKeg8dgfor3Ry9P3C8HjedDmfkuic4kXSc24Jb8dY9bxVp\nf8V2V6qgoCBiY2Otj8+ePUtQUNAVz0dHRxMYGHgzL2XXTCYT6enppKenc+jQQQAaNWrCr79uAODv\nv4+wbNlnN7W//NSoUZPjx4+RmppKRkYGzz47AsMwMJmcyM7Otq7n6+uLyWTizJkzAOzatYMGDRre\nQKciIo7PkmNh5pZXeeCr7pxKPskLLcfyzb/WUKt8rRKr4aZGzlWrViU5OZmTJ09SsWJF1q9fz5w5\nc0hISGD+/Pn07duXffv2ERQUdFPHm+3dAw/0ZujQx6hZszb16+eGXu/eDzNt2hRGjBhCTk4Ozz47\n+qb2lx9PT08GDx7Gs8+OAODhh/+NyWSiefMWjBgxmAkTpljXnTp1Ki+/PAFnZ2eqVKnKnXfexdq1\nP9xYwyIiDurvxCOMWPcE289upbpPDd4JXUibSm1LvA6TUcicc0REBLNmzeLUqVO4uLgQHBxM165d\nqVq1Kt26dWPr1q3MmTMHgLvuuovBgwcDMGfOHLZt24bJZGLy5Mk0aNCgwEJsPRXiaNMxl3P0/sDx\ne1R/pZuj9welu0fDMFh+cAnjf3uRlKxkHqrbh1kd5+Lr7mddp6j7K2hau9BwLim2fkNL83+qa+Ho\n/YHj96j+SjdH7w/ss8fYtFheDZ/Ml4dX4Orkho+bD96u3ni7eVPO9Z9/x6bF8PPxdfi4+TKr41x6\n13v4in2VZDjrCmEiIuJwcowcPtv/Ca9umsy5jHNU96lBOVdvUrKSiUmL5u/EI2TmZObZplXFNrwb\nupAavjVtU/QlFM4iIuJQdkfvZOyvz7Mjejverj682mEmg24ZiotT3sjLzM4kOSuJ5MxkMrMzqe0f\ngpPJPm45oXAWERGHkJhxjhmbp/LxvkXkGDk8WLc3U9pPo2K5Svmu7+bshtk5ALNHQAlXWjiFs4iI\nlGqGYbDi0HImb5xAbFoMdfzrMrPjXDpW7Wzr0m6YwllEREqtwwl/8eIvz/JH1G94ungyoc1kht/6\nFG7O+V9aubRQOBfg9OkoBgzoS/36uR8Dy8zM5JFHHqNTpy7Xva8vvljOuXPn6NixM7/+uoHBg5/M\nd72Lt3t0dXUtdJ9Hjhxm3rzZV9xmslOnNtxySzPr44CAAN599+3rrvly69evo0uXUP7662CBPYiI\nFLeM7Azm73idN7bPITMnk7trdmfa7bOp7lvD1qUVCYVzIapXr2ENv/PnE3n88Udo27Yd7u4eN7S/\nunXrU7du/asuv3i7x2sJ56vx9vYukvtCX+6zzz6hS5fQQnsQESlOm6I2MvqXZziUcJCK5Sox/fbX\n6Fm7FyZT0d5/wZYUztfB19ePgIAKxMXF8Z//LMTFxZXz58/xyiszmT17GlFRp7BYLAwZMozbbmvF\ntm1beOutuZjNAQQEVKBy5Srs2LGNlSv/x6uvzi7wdo9vvvkeq1Z9ybp1qzGZnLjjjs7069ef6Oiz\nTJw4DldXV+rUqXfNtZ88eZIRI0axaNGnAAwe/CivvjqLjz76gAoVAjl48E/Onj3DpEmvUr9+AxYv\n/oQNG37CZHJi2LBRHDiwn8OHDxEW9iK9ez9s7eGnn35k+fLFODs7U79+Q559djSLFi3I9/aWIiI3\n41x6AlM3TebT/R9jwsSgJk8Q1mZSnguFOIpSE87lpryE+zdFe8vIjF4PkDLl2m8Zefp0FOfPJxIU\nFAzkXrN67NgJrF79HQEBFRg/fhLnzp3jmWeG8ckny1iw4G0mTpxK3br1GD36aSpXrmLdV2pqSoG3\ne4yJiWbDhp94991FAAwfPpguXUJZuXI5d955F3369OOzzz7m8OFDN/19yMzMZN68t/nqqxWsXv0d\nXl5ebNjwEwsWfExU1Ck+++xjxo2byOLFnzB9+mvs2LHtQg+pfPDBO/znP0vw8vJizJjnrMsuv72l\nwllEbpRhGHx9eCUTfh9LTFo0Dc2NmNv5LVpWbG3r0opNqQlnWzl+/BijRg0Fcu9t/dJLL1tvodmo\nUe5tMSMi9rB790727NkFQEZGBllZWZw+fZq6dXNHt7fe2oKMjAzrfo8e/Zvq1Wvi7u6Bu7sHM2fO\ny/O6f/65j5MnT/DUU7nHdVNTUzhzJoqjR/+mS5fce2U3b96STZs2XlFzcnKytWaAkJA6jBhx9ePD\nzZo1ByAwMJj9+/dx6NBBGjVqgpOTE1WrVmPcuIn5bnfixHGqVq1uvatW8+a3cejQAQCaNr0VyL05\nSnJy8lVfW0SkIHFpcTzz83DWHluNh7MHL7WdwvBmT+HqfOOH/kqDUhPOKVNeva5RblG59Jjz5Vxc\nXK1fBwwYRLdu9+RZ7uT0z4fZL79KqpOTM4aRc9XXdXFxpV27DowZMyHP84sXf4Lpwofkr7Z9fsec\nMzPP53lssVis/754P+mLdTo7O5GTU/hVXU2mvH1ZLFm4u7vnu08Rkeu1N2Y3A1c/womk49xRtTNz\nOr1BLb/ati6rRNjHpVBKuUaNmvD7778AkJAQz4IF7wBQoUIgx48fxTAMdu7cnmebwm73WL9+Q3bs\n2E56ejqGYfDGG3PIyEinevUaHDiwH8A6hXwtvL29SUiIxzAM4uJiiYo6edV169dvyN69u7FYLMTH\nxzF+fO4dtS4P7GrVanDy5HFSU1MA2LlzB/XrN7rmmkREruZ/B5fSc2U3TiQd58VW4/m811dlJpih\nFI2c7VnXrqHs2LGVYcMGkZ2dzaBBuVPKQ4eO4KWXxlKxYiXrceqLCrvd4/z5H9CnTz9GjnwCJycn\nOnbsjLu7B//3f/2YOHEcv/66npCQutdco5+fHy1btmbIkAHUqVO3wLOtK1WqzN1392DUqKEYhsGT\nT44EoF69+jzxxACGD3/a2sPIkc/wwgtPYTI50bTprTRrdivbtm2+ru+fiMhFWdlZvBz+Eh/seQ8f\nN18+vPsT7qrZ3dZllTjdleoCe7ybSlFy9P7A8XtUf6Wbo/cHN99jTGoMT6x9jI1Rv1O/fAM+7r6Y\nEP9rH4QUN92VSkREypSdZ7fz+Or+RKWc4t7a9/NW13fxdrt6eDk6hbOIiNhMjpHD0j8/Y9xvL5CZ\nnclLbafwVPPnHOqCIjdC4SwiIiUmMzuTPTG7CD+9kc1RG9lyZhPnMs7h7+7PJ92X0rV6qK1LtAsK\nZxERKTaZ2ZlsOr2RTVEb2XR6I9vPbiXNkmZdXsO3Jt1r3ctzt71ITb9aNqzUviicRUSkyBmGwTeR\nX/HKpskcP38UABMmGpgb0bZyO9pV6kCbSu2o5F3ZtoXaKYWziIgUqe1ntzLpjzC2ntmMq5MrjzUe\nTLcad9G6Ylv8PcrburxSQeEsIiJF4ti5Yzz/42hW/rUCgB61ejGp3cvU9q9j48pKH4WziIjclKTM\n87y5fR4L9rxDRnYGzQKb80qH6bSrrBve3CiFs4iI3JCs7Cw++/MTXts6ndi0WKr6VmV8q0k8VK8P\nTiZdHfpmKJxFROS6ZOdk8+XhFczaMo1j54/i5VKOca1fYmLoeFLOZdu6PIegcBYRkWtiGAZrjv7A\njM2v8Gf8flydXBl8y1Ceve1Fgr2C8XL1IgXHvkRpSVE4i4hIoX4/9SvTNr3M9rNbcTI58XD9f/Ni\nq/FU961h69IcksJZRESuaufZ7Uzf/Aq/nFwPwL2172ds6wnUNzewcWWOTeEsIiJXSM1KZfrml/lg\nz3sAdK7WlbA2k7g1qIWNKysbFM4iIpLHtjNbeOrnYUSeO0xd/3rM6jSP26t0tHVZZYrCWUREAMjI\nzmDu1lm8tXMehmEwrNkoxreZiKeLp61LK3MUziIiQkTsXkb99CT74yKo7luTt7q8S/sqt9u6rDJL\n4SwiUoZZcizM3/E6c7bNJCsniwGNBjGl/VS83XxsXVqZpnAWESmjjiRGMuLHIeyI3k7FcpV4o8vb\ndK3ezdZlCQpnEZEyafXf3zPqpyc5n5nIQ3X7MOOO13THKDuicBYRKUOyc7KZtWUab+yYg6eLJ2/f\nuYA+9fvZuiy5jMJZRKSMiE2LZdiPg/n15Hpq+tbiP/cspnGFJrYuS/KhcBYRKQN2nN3G4DUDOJV8\nkrtrduftOxfg5+5v67LkKnRPLxERB2YYBh9HLOK+L+8hKvkUYW0m8Un3pQpmO6eRs4iIg0rNSmXs\nr8+z/OASzB5m3gtdRJfqd9q6LLkGCmcREQeRmZ3JzugdhEf9TnjUH2w5s5mUrGRuDWzOons+pZpP\ndVuXKNdI4SwiUkqlWdLYcXYbG6N+Z1PURrad3UKaJc26vK5/PbrXupfRrcbh4eJhw0rleimcRUTs\nXFZ2FpGJhzkY/yd/xu/nYPwBDsb/yZHESHKMHOt6Dc2NaV+lA+0qdaBt5Q4EeQXZsGq5GQpnERE7\nFJV8iumbX2FPzC4izx0mKycrz3J/d39aVWzDrUEtaF/5dtpUaovZI8BG1UpRUziLiNiZY+eP8tDX\nvTiedIxyrt40DWxGA3Mj6psb0MDciAbmhgR7VcRkMtm6VCkmCmcRETty5NxhHvy6F1EppxjTKowX\nWo5VCJdBCmcRETtxMP4AD63qRXTqWSa1m8qo5s/YuiSxEYWziIgdiIjdy/+tuo+49Dim3z6bIU2H\n2boksSGFs4iIje08u52Hv/0XiRmJzOn0JgMaP27rksTGrimcp0+fzu7duzGZTISFhdG0aVPrsnXr\n1vHee+/h5uZGz5496d+/P5s3b+aZZ56hbt26ANSrV4+JEycWTwciIqXYltOb6ffdQ6RkJfNW1/d4\nuMG/bV2S2IFCw3nLli0cO3aM5cuXExkZSVhYGMuXLwcgJyeHqVOn8uWXX+Lv788TTzxBaGgoAK1b\nt+att94q3upFREqxP079xiPf9SEjO533QxfxQN2HbF2S2IlCb3wRHh5uDdyQkBASExNJTk4GICEh\nAV9fX8xmM05OTrRt25aNGzcWb8UiIqVcVnYWi/f/l37fPkRWTiYf3v1fBbPkUejIOTY2lsaNG1sf\nm81mYmJi8Pb2xmw2k5KSwtGjR6lSpQqbN2+mdevWVKlShcOHDzNs2DASExMZNWoUHTp0KPB1ypf3\nwsXF+eY7ugmBgT42ff3i5uj9geP3qP5KN29/FxbtXMRrG1/jeOJxPFw8+Orhr+hRt4etSysyjv4e\nllR/131CmGEY1n+bTCZmzpxJWFgYPj4+VK1aFYCaNWsyatQounfvzokTJxgwYABr167Fzc3tqvtN\nSEi9gfKLTmCgDzExSTatoTg5en/g+D2qv9LrfEYi//v7U+aFv05sWgyeLp4MueVJRtz6NFV9qjlM\n3478HkLR91dQ0BcazkFBQcTGxlofR0dHExgYaH3cunVrlixZAsDcuXOpUqUKwcHB9OiR+5dg9erV\nqVChAmfPnqVatWo33ISISGkTkxrDB3ve5aOIhSRlnsfXzY9nW4zmiabDCfQKLHwHUmYVGs4dOnRg\n/vz59O3bl3379hEUFIS3t7d1+ZAhQ5g1axaenp6sX7+exx9/nFWrVhETE8PgwYOJiYkhLi6O4ODg\nYm1ERMTWEjPOERG7l72xu9kVvZPvj3xDenY6FTwDCbtzBv9Xsz++7n62LlNKgULDuUWLFjRu3Ji+\nfftiMpmYPHkyK1euxMfHh27dutGnTx8GDRqEyWRi6NChmM1munbtyujRo/npp5/IyspiypQpBU5p\ni4iUJoZhcCblNHtjd7M3dg97Y/YQEbeX4+eP5lmvmk91Rtz6NP9u+CjVKwU59JSvFC2TcelBZBuy\n9X9aHSsp/Ry9R/VnG4ZhcDolit0xu9gds5M90bvYHbOLmLToPOtV8KxAkwpNaVKhKbdUaMotFZpR\n2z8EJ1Puh2Lstb+i5Og92tUxZxGRsiY+PY4P9yxgZ/R2dsfsIjYtJs/yKt5V6V7rXpoGNrMGccVy\nlXSDCikyCmcRkUukZKXQ95sH2RWzE4Cq3tXoUasXzQJvpVnQrTQNbE4Fzwo2rlIcncJZROSC7Jxs\nhv84mF0xO+lTvx8vt59OgGeArcuSMkjhLCJC7rHliX+MY/XR77mjamfmdZ6Pm7NOZBXbKPTynSIi\nZcGCPe/w4d4FNDQ34j93f6pgFptSOItImfdN5NdM/mMCwV4VWdzzc30WWWxO4SwiZdrWM5sZue4J\nPF28WNLzc6r66EqGYns65iwiZdaRxEgGfN+XrJwsPu3xKbcENrN1SSKAwllEyqi4tDj+/W1v4tLj\neK3TG4TWuNvWJYlYaVpbRMqcdEs6j/3QjyOJkTzV/DkeazzI1iWJ5KGRs4g4vHRLOhGxe9gZvZ0d\nZ7ez9cxmjicd4191HmJC28m2Lk/kCgpnEXE4J5KO89vJX9gZvYOd0dvZHxeBJcdiXe7r5kfveg8z\nr/N867WvReyJwllEHMr3R77lyR8fJyM7AwB3Z3eaBTaneVALmgfdRovg26jlF6JQFrumcBYRh7F4\n/3954Zen8XD2ZGqHKbSt1J6GAY11QREpdRTOIlLqGYbB/J1v8OqmyZg9zCzu+Tm3BbeydVkiN0zh\nLCKlWo6Rw5SNL/H+7rep4l2V5fd+ST1zfVuXJXJTFM4iUmplZWfx7PqRfH5oGfXK12f5vV9Sxaeq\nrcsSuWkKZxGxK+uP/8S3R1bRpMIttK98O/XK18dkMl2xXmpWKk+sfYwfj63htuCWLO75OWYP3d5R\nHIPCWUTsgmEYvLXjdaZtmoKBYX0+wCOAtpU70L5yB9pVvp1GAY05n5HII9/3YeuZzXSpdieL7vkU\nb1dvG1YvUrQUziJic2mWNPp/OYwle5dQqVxl5nZ+k9Mpp9l46nfCo/7guyOr+O7IKgD83f3xcilH\nVMopHqzbm7e6vq+zscXhKJxFxKZOJ0fx2A/92BWzk9uCW/Fx9yUEewUD8GijgRiGwfGkY4RH/cHG\nqN/ZGPUHJ5OOM7TpcF7pMEOfVxaHpHAWEZvZfnYrA394hLOpZxh460CmtnkNd2f3POuYTCZq+Nak\nhm9N+jZ4BICM7Iwr1hNxJPqTU0Rs4n8Hl/LAVz2ISYvmlQ7T+ei+j645cBXM4ug0chaREpWdk82r\nm6bwzq438XXz45PuS+laPTTfM7JFyiqFs4iUmEPxBxn32wv8fupX6vjX5dMeywjxr2vrskTsjsJZ\nRIrd+YxEXts2k0V7F2DJsXB3ze68fecC/Nz9bV2aiF1SOItIsckxclh2YDGvbppCbFoMNXxrMrXD\nTO6u2V3T2CIFUDiLSLHYdmYLE34fw87oHXi5eBHWZhLDmo3Cw8XD1qWJ2D2Fs4gUqbMpZ3h10xSW\nH1wCwIN1ezOp3VQqe1excWUipYfCWUSKhGEYLDuwmAm/jyU5K4kmFZoy/fbZtK3c3taliZQ6CmcR\nuWnRqdG8sOEp1hz9AW9XH2Z3fJ1HGw3E2cnZ1qWJlEoKZxG5Kd9Efs2YX54lLj2O26t05M2u71LN\np7qtyxIp1RTOInJDEjPOEfbbGD4/tAwPZw9e7TCTIU2H6VrXIkVA4Swi1+2XE+t55ucRRKWc4tbA\n5rwTupC65evZuiwRh6FwFpFrlpqVytRNk1i09wNcnFwY0yqMZ1q8gKuzq61LE3EoCmcRuSb74/bx\n5NrHOZhwgHrl6/POnR/QLKi5rcsScUg6OCQiBTIMg48iFnL3is4cTDjA4FuG8uP//apgFilGGjmL\nyFUlpMfz7PpR/PD3t5g9zHx493+5u2Z3W5cl4vAUziKSr/CoPxj+4xCiUk7RofIdvBu6kErelW1d\nlkiZoHAWkTwsORbmbZvNvO2zMWFifOuJPN3ieV1QRKQEKZxFBMg9tnww4QBjfnmOTac3UtW7Gu93\n+4jWldrYujSRMkfhLFKGWXIsbDm9idVHv2ft0R84khgJQK+QB5jb6U38PcrbuEKRsknhLFLGnM9I\nZP2Jn1j99/f8dHwt5zLOAeDlUo6ete/jwbq9ubf2/brfsogNKZxFygDDMPjl5HoW7nmPDSd+Jisn\nC4BK5SrzQJ2HuKdWD9pXvkP3WhaxEwpnEQeWkZ3BykOf8/7ut/kzfj8At1Roxj21enBPzR40qdBU\nI2QRO6RwFnFA8elxfByxiEV7PyAmLRpnkzMP1u3NsGajuDWoha3LE5FCKJxFHEjkub94f/e7/O/g\nEtIsafi4+TLi1qd54pZhVPGpauvyROQaKZxFSrl0Szo//P0tn/35X347uQGAaj7VGdp0OI80HIC3\nm49tCxSR63ZN4Tx9+nR2796NyWQiLCyMpk2bWpetW7eO9957Dzc3N3r27En//v0L3UZEbt6B+D9Z\nvP8T/ndwKQkZCQC0rdSeIbc8SY/avXBx0t/eIqVVoT+9W7Zs4dixYyxfvpzIyEjCwsJYvnw5ADk5\nOUydOpUvv/wSf39/nnjiCUJDQzl+/PhVtxGRG5eclcyqw1/y6f6P2X52KwAVPCsw8tZneKThAOqU\nr2vjCkWkKBQazuHh4YSGhgIQEhJCYmIiycnJeHt7k5CQgK+vL2azGYC2bduyceNGTpw4cdVtROT6\nWXIszPhtBtN+m05KVjImTHStHkr/hgO5q+Y9uDm72bpEESlChYZzbGwsjRs3tj42m83ExMTg7e2N\n2WwmJSWFo0ePUqVKFTZv3kzr1q0L3OZqypf3wsXFttfuDQx07GNzjt4fOGaPkfGRPLrqUcJPhhNc\nLpjR7V9gUPNBVPerbuvSipwjvn+XcvT+wPF7LKn+rvuglGEY1n+bTCZmzpxJWFgYPj4+VK2a/9mg\nl25zNQkJqddbSpEKDPQhJibJpjUUJ0fvDxyvR8Mw+OzPT5j4+3hSLSk83PhhXmkzi/IeZsjEoXoF\nx3v/Lufo/YHj91jU/RUU9IWGc1BQELGxsdbH0dHRBAYGWh+3bt2aJUuWADB37lyqVKlCRkZGgduI\nSMGiU6N5fv0o1h5bjZ+7P+93WcST7Qc59C8+EfmHU2ErdOjQgTVr1gCwb98+goKC8kxPDxkyhLi4\nOFJTU1m/fj3t2rUrdBuRsmhv7B42n95EbFpsgbNJ3x/5lk7L2rD22GruqNqZXx4O58G6/1eClYqI\nrRU6cm7RogWNGzemb9++mEwmJk+ezMqVK/Hx8aFbt2706dOHQYMGYTKZGDp0KGazGbPZfMU2ImXZ\ngt3vMPGP8dbHfu7+hPiFUNu/DrX9Qgjxr0NN31p8vG8RSw98hoezB9Nun8XgW57EyVTo39Ai4mBM\nxrUcEC4Btp6u07GS0s9ee1yQT4X5AAAgAElEQVS45z0m/D6WYK+KPFSvD0cSIzly7jB/Jx6x3oDi\nUk0Db+XdOxdSz1w/z/P22l9RUX+ln6P3aFfHnEXkxi3au4AJv48lyCuYL+//Ls/nkLNzsjmRdNwa\n1pGJh6nmU4Mhtzypj0aJlHEKZ5FismjvB4z/7UUCPYOuCGYAZydnavrVoqZfLbpWD7VRlSJij3Qw\nS6QYfByxiPG/jaaCZyBf3v8ddcvXs3VJIlKKKJxFith/9/2HMb8+RwXPCnx5/3dXHDsWESmMwlmk\nCH22/xNG//IMFTwr8MV931Lf3MDWJYlIKaRwFikiS/78lOc3PEWARwAr7vuGhgGNbF2SiJRSOiFM\n5CYlZZ5nztZZvL/7bcweZlbc9w2NAhoXvqGIyFUonEVukGEYfPHX/3h540TOpp6hum9NPr5nMY0r\nNLF1aSJSyimcRW5AROxexv82ms2nw/Fw9mBs6wmMuPVpPF08bV2aiDgAhbPIdTiXnsCsrdP4T8SH\n5Bg59KjVi1c6TKe6bw1blyYiDkThLHINcowclvz5KdM2TSEuPY4Q/zpMu322Lh4iIsVC4SxSAMMw\n+PHYamZumUZE7B68XMoxsd0rPNl0hC6xKSLFRuEschW/n/qV6ZteYdvZLZgw8VDdPkxq9wqVvCvb\nujQRcXAKZ5HLbD+7lembp/LbyQ0A9KjVi7GtJ+hzyyJSYhTOIhfsi41g1pZXWX30ewA6V+vK+NYT\naR58m40rE5GyRuEsZV5yVjLjfx3N/w4uxcCgTaV2hLWZRLvKHWxdmoiUUQpnKdP+TjzCwB/+zZ/x\n+7mlQjMmtJ1El2qhmEwmW5cmImWYwlnKrPXHf+LJHx/nXMY5Bt8ylFfaz8DV2dXWZYmIKJyl7DEM\ng3d3zWfqpkm4mFx4s8u79GvY39ZliYhYKZylTEnNSuX5DaNY+dcKKparxH/u+YzbglvZuiwRkTwU\nzlJmHD9/jIGrHyEidg+tKrbho3s+I9gr2NZliYhcQeEspVpmdiYzNk9l+cElVCgXQKB7MBXLVaJS\nucpU8q5EsFclKnlXIi4tlqd/Hk58ejyPNnqcGXe8pit8iYjdUjhLqXU08W+e/PFxdkbvIMAjgNjU\nWA7EHrjq+q5OrrzW6Q0eazyoBKsUEbl+Cmcplb4+vJLnNzxNUuZ5+tTvx8yOc6lVuRInz8RyJuU0\np1NOczblNKdTojidfJrzmYn0a/AorSu1sXXpIiKFUjhLqZKalcrEP8bx6f6P8XIpx/yu7/Nwg39b\nl7s7u1PDtyY1fGvarkgRkZukcJZS42D8AZ5Y+xgH4v+kccAtLLzrY+qUr2vrskREipyTrQsQKYxh\nGCze/1/uWtGJA/F/MqjJE/zw0E8KZhFxWBo5i1279GYUfu7+vBv6IT1r97J1WSIixUrhLHYpInYv\nc7fN4rsjqwBoW6k974R+QDWf6jauTESk+Cmcxa7sjd3D3K2z+P7vbwC4LbglL7Yar5tRiEiZonAW\nu3BlKLe6EMp3KpRFpMxROItNRSWf4qXfx/Htka+B3FAe0yqMztW6KpRFpMxSOItNGIbBZ39+wpSN\nL5GUeV6hLCJyCYWzlLjj54/x/Ian+fXkenzcfHm989v8u+GjCmURkQsUzlJicowc/hPxIVPDJ5Nq\nSSG0+l3M6fwmlb2r2Lo0ERG7onCWEnEkMZLn1o8iPOoP/N39md1pAf9Xr69GyyIi+VA4S7HKzslm\n4d73mLF5KmmWNLrXupfZHecRXK6irUsTEbFbCmcpNtGp0YxY9wS/nlxPgEcAb3Z5l/vrPKjRsohI\nIRTOUix+O/kLw9cNITr1LHfVuIfXu7xDoFegrcsSESkVFM5SpLJzspm7bRZzt83C2cmZKe2nMbzZ\nKI2WRUSug8JZiszZlDMMXzeE30/9SjWf6izo9hEtK7a2dVkiIqWOwlmKxIYTPzNi3RPEpsVwT62e\nvNXlXfw9ytu6LBGRUknhLDfFkmNhztYZvL59Di5OLkztMIOhTUdoGltE5CYonOWGRSWfYvi6IYRH\n/UF1nxosvOtjmgffZuuyRERKPYWz3JC1R3/g6Z+HE58eT8/a9/FGl7fxc/e3dVkiIg5B4SzXJTM7\nk6mbJrNg9zu4O7szq+M8BjYerGlsEZEipHCWa/Z34hGeXPs4u2J2Use/Lh/c9TFNKtxi67JERByO\nwlmuyVd/fcHzG54mOSuJh+v/mxkd5+Dt6m3rskREHNI1hfP06dPZvXs3JpOJsLAwmjZtal22ePFi\nVq1ahZOTE02aNGHChAmsXLmSN998k+rVqwPQvn17hg8fXjwdSLFKzUpl4h/j+HT/x3i5lOPtOxfQ\np34/W5clIuLQCg3nLVu2cOzYMZYvX05kZCRhYWEsX74cgOTkZBYtWsTatWtxcXFh0KBB7Nq1C4Ae\nPXowduzY4q1eikW6JZ0/Tv3K2mOrWf3395xOiaJxwC0svOtj6pSva+vyREQcXqHhHB4eTmhoKAAh\nISEkJiaSnJyMt7c3rq6uuLq6kpqaipeXF2lpafj5+RV70VL0zqac4cdja1h7bDW/nlhPqiUVAD93\nf4Y1G0VYm0l4uHjYuEoRkbKh0HCOjY2lcePG1sdms5mYmBi8vb1xd3dn5MiRhIaG4u7uTs+ePalV\nqxY7d+5ky5YtDB48GIvFwtixY2nUqFGBr1O+vBcuLs4339FNCAz0senrF7XTSaf57+7/kpGdAYBh\nGLlfMazrpGWl8fPRn9kWtc36XP2A+vSq14t7691L+2rtcXV2LdnCb4KjvYeXU3+lm6P3B47fY0n1\nd90nhF38BQ+509oLFixg9erVeHt789hjj3HgwAGaNWuG2Wymc+fO7Ny5k7Fjx/LNN98UuN+EhNTr\nr74IBQb6EBOTZNMailJU8inu/6o7x84fLXRdFycX7qjSibtq3kO3GndT27+Oddm5+HQgvfgKLUKO\n9h5eTv2Vbo7eHzh+j0XdX0FBX2g4BwUFERsba30cHR1NYGDurf8iIyOpVq0aZrMZgJYtWxIREUHv\n3r0JCQkBoHnz5sTHx5OdnY2zs21HxmXFmZTTPPj1vRw7f5SRtz5D1+qh+Pt7ce5cap7PI5sw4WRy\nonFAE3zddThCRMReFBrOHTp0YP78+fTt25d9+/YRFBSEt3fuR2iqVKlCZGQk6enpeHh4EBERQadO\nnVi4cCGVKlXi3nvv5dChQ5jNZgVzCYlOjeahr3txJDGSZ1q8QFibSZhMJof/i1ZExJEUGs4tWrSg\ncePG9O3bF5PJxOTJk1m5ciU+Pj5069aNwYMHM2DAAJydnWnevDktW7akatWqvPjiiyxbtgyLxcK0\nadNKopcyLzYtlt6revHXuUMMb/aUNZhFRKR0MRmXHkS2IVuP6kr7yDI+PY4Hv+7F/rgIhjYdztQO\nM/MEc2nv71o4eo/qr3Rz9P7A8XssyWPOTkX2KmIz59IT+L9VD7A/LoLHmwy5IphFRKR0UTiXcucz\nEnn423+xN3Y3jzYayIw75iiYRURKOYVzKZacmUTfbx9iZ/QO+jZ4hNc6vYGTSW+piEhppxtflDI5\nRg5bzmzmu8ivWRX5FadTouhd72Fe7/y2gllExEEonEuB7JxsNp3eyDeRX/HdkW84m3oG+OfSmpPa\nvYKzkz6qJiLiKBTOdiohPZ7tZ7fyw9/f88Pf3xCblnshGLOHmUcaDqBXyP3cXqUTbs5uNq5URESK\nmsLZDqRb0omI3cPO6O3sOLudHdHb+DvxiHV5Bc9AHms8mF4h99O+8u24OOltExFxZPotbyMnko7z\n3q75bDuzhX1xEWTlZFmX+bn707laV5oHtaBj1S60rdRe09YiImWIwrmEZedks2jvAqZvnkqqJQU3\nJzduqdCUFsEtaR50Gy2Cb6OWX4hO7hIRKcMUziXoQPyfPLd+FNvPbqW8e3lmdpzDv+r2xt3Z3dal\niYiIHVE4l4CM7Aze3D6XN3fMJSsni3/VeYhXb59NoFegrUsTERE7pHAuZlvPbOb59U9xMOEAlctV\nYXanedxVs7utyxIRETumcC4myVnJzNj0Ch/uXYCBwcDGg5nY7mV83HxtXZqIiNg5hXMxSEiPp883\n/2J3zE7q+NdlXpe3aVupna3LEhGRUkLhXMTi0+P4v1UPsDd2N/0a9GdWx3l4uHjYuiwRESlFFM5F\nKDYtlt6r7mN/XASPNnqc1zq9ro9EiYjIdVNyFJGY1Bge+vpe9sdFMLDxYAWziIjcMKVHEYhOjebB\nr3vyZ/x+htzyJLM6zlMwi4jIDVOC3KSzKWf411c9OJhwgCebjmDa7bMxmUy2LktEREoxhfNNOJ0c\nxQNf9+Cvc4cY3uwpXukwQ8EsIiI3TeF8g04kHeeBr3sQee4wTzV/jintX1Uwi4hIkdDZ2vnIzsnm\ny8Mr+DvxCPHpccSnxRGXHk98ehwJF76mWdIAeLbFaMa3mahgFhGRIqNwvkx8ehzDfhzMhhM/X7Gs\nnKs3AR4B1C/fALNnAN1q3MOgJk8omEVEpEgpnC+xN3YPj//wCMeTjtGtxt0MbTqCAM8KBHgEUN7D\nrIuJiIhIiVA4X7Bk7xKGrBpCmiWNF1qO5cVW4/VxKBERsYkyH86WHAsvh09kwe538Hb14b/dl3FP\nrR62LktERMqwMh3OMakxDF07kD+ifqNhhYYs6vYZdcrXtXVZIiJSxpXZcN4VvYPHV/fnVPJJeta+\nj6V9PiP9vK2rEhERKYOfc07NSuX1ba/R68u7iUo+xYQ2k/no7k/xcfexdWkiIiJAGRo5W3IsLD3w\nGbO3TOds6hkCPAJ4p/sHdK3ezdaliYiI5OHw4WwYBquPfs+0TVM4lHAQTxdPnrttNKOaP4uPm6+t\nyxMREbmCQ4fz1jObeSV8EptPh+NkcuLRRgN5sdV4KparZOvSRERErsohw/lE0nEm/RHGd0dWAXBP\nrZ681GYK9cz1bVyZiIhI4RwynF/eOJHvjqyiVcU2TGo3lTaV2tq6JBERkWvmkOH8UtspDGwymA6V\n79B1r0VEpNRxyHCu6VeLmn61bF2GiIjIDSlzn3MWERGxdwpnERERO6NwFhERsTMKZxERETujcBYR\nEbEzCmcRERE7o3AWERGxMwpnERERO6NwFhERsTMKZxERETujcBYREbEz13Rt7enTp7N7925MJhNh\nYWE0bdrUumzx4sWsWrUKJycnmjRpwoQJE8jKymLcuHFERUXh7OzMjBkzqFatWrE1ISIi4kgKHTlv\n2bKFY8eOsXz5cqZNm8a0adOsy5KTk1m0aBGLFy9m6dKlREZGsmvXLr799lt8fX1ZunQpw4YNY+7c\nucXahIiIiCMpNJzDw8MJDQ0FICQkhMTERJKTkwFwdXXF1dWV1NRULBYLaWlp+Pn5ER4eTrdu3QBo\n3749O3bsKMYWREREHEuh4RwbG0v58uWtj81mMzExMQC4u7szcuRIQkND6dKlC82aNaNWrVrExsZi\nNptzX8DJCZPJRGZmZjG1ICIi4liu+37OhmFY/52cnMyCBQtYvXo13t7ePPbYYxw4cKDAba6mfHkv\nXFycr7ecIhUY6GPT1y9ujt4fOH6P6q90c/T+wPF7LKn+Cg3noKAgYmNjrY+jo6MJDAwEIDIykmrV\nqllHyS1btiQiIoKgoCBiYmJo0KABWVlZGIaBm5tbga+TkJB6M33ctMBAH2JikmxaQ3Fy9P7A8XtU\nf6Wbo/cHjt9jUfdXUNAXOq3doUMH1qxZA8C+ffsICgrC29sbgCpVqhAZGUl6ejoAERER1KxZkw4d\nOrB69WoA1q9fT5s2bW66CRERkbKi0JFzixYtaNy4MX379sVkMjF58mRWrlyJj48P3bp1Y/DgwQwY\nMABnZ2eaN29Oy5Ytyc7OZuPGjfTr1w83NzdmzpxZEr2IiIg4BJNxLQeES4Ctp0I0HVP6OXqP6q90\nc/T+wPF7tKtpbRERESlZCmcRERE7o3AWERGxMwpnERERO6NwFhERsTMKZxERETujcBYREbEzCmcR\nERE7o3AWERGxMwpnERERO6NwFhERsTMKZxERETujcBYREbEzCmcRERE7o3AWERGxMwpnERERO6Nw\nFhERsTMKZxERETujcBYREbEzCmcRERE7o3AWERGxMwpnERERO6NwFhERsTMKZxERETujcBYREbEz\nCmcRERE7o3AWERGxMwpnERERO6NwFhERKYxhlOjLuZToq4mIiEBu2GVnQ2YmpqxMyLLkfs3MxJSV\n9c/zlz/OZz0sWZgysyArE1NmJmRlXfia+c/zWVl5H+dZ72rrZ/3zWhYLPPkkTH2tRL49CmcREUdh\nGJAn2LLyBpk1bC4Nnawr18tve4ulgP1eCDty8E9JgwLD9pJtS3g0mu+3zNUVXN0ufHXFcHMDNzdy\nvL1zn3f7Z7lbmzYlVpfCWUSkIBdHd1eEWMEBdMXozMMZz/ikS56/2ijuwvOWAkZ1l4/6si5+zbL1\ndwsXkwnc3DBc3cDNNferqytGuXIYbuWtz+NyIQhdXXOD0c39wtfLtnVzw3BxyX+fl65/SbDmPnb5\nZ3tr8Lrn2S+urmAyXXNvgYE+EJNUjN+9fyicRaRkGQZYLFeO4pLccD6TcJXR2TWOxC6b/ix4mvMa\nR4Y5OUXWuveNfssuDaeLIeTiSo6nZ26ouV3yvPXrhVGfiyuGu/uFMLwwCnTLux/DPferNcguDTgX\nV3C/PDgvWc/FFdxzvwZWCSA2PvW6Ak/yp3AWcQQ5OXmPj+UXXlmXjPwKG7UVeowun+cLWv+SUWfu\n9Gf+zCX4LTPyG6F5emL4+VmDKU/wXZz+vGSaM29gXnz+4j4vCUZXV3wr+JGYlp13PVeXC6O5fEZ6\nF4PPzQ2cSsm5uy4uCuYionAWyc/lJ6tkZl2Y1izkZJXMy6YY8wvIQqcpL3veYsn9mmPBnJbxz6jv\n0pGkxWLr7xiGs3PekZRr7ugtx8/zymN6F0drF0dxLi54+JYjLdtkHe1dMYq7fJrT3T2fac4Lj/Md\n7V0ynensXPIhEuhDZglNiUrpp3CWknNhdJfvSSn5BlkmpizLNQThhTBzNeGdmJw35K4ytXn1sLWz\nk1UuCZbcUMkNpRwfn7zTlpcfu7v8+YvTnBfD6tJpz0sC8mJwWsM1v4C8GHwurnmCEWfnm+rVI9CH\nZIWXCKBwLv0uH91dHmIXAohyrrhGn7vqevl+FCHrWqY9r/FklRIa3XkWstwwmfKOuC6O0Ly8MNzL\nXzYSuzjteDHYLkxzXj6KyzMFmc/zl7/W1ba/fJrzsinCwEAf4hVeImWCwvlyl38U4bpPQrnKdObV\nTji5WsBd68cgruNkFf/i+pY5O/8TeJeclJJTrlzu6C3PaC2fk1UuHe1dfrLK5Se1XPJ8nmN0Li6U\nr2gmPjnrsuDLG4w3O7oTESkJDhnObmt/wGPp4vxHfVeb5szKosLFELQDxuXThpefrHL5SSmXju4u\nDbgLwefl701KllHIRxQKmsLM/6MMuLraz8kqgT5ka2QpIg7AQcN5De7frcrznPVklTwjKXfrySpO\nXh5YTM6XfCD9sjM1LztGl+djCwVNc7q7XTKdednZnfmd1FJMJ6t4BfqQquASESkVHDKck197nZSw\nif8E5DWcrBIY6MM5hZeIiNgBhwxnTCYMc4CtqxAREbkhdnKwUERERC5SOIuIiNgZhbOIiIidUTiL\niIjYGYWziIiInVE4i4iI2Jlr+ijV9OnT2b17NyaTibCwMJo2bQrA2bNnGT16tHW9EydO8MILL5CV\nlcWbb75J9erVAWjfvj3Dhw8vhvJFREQcT6HhvGXLFo4dO8by5cuJjIwkLCyM5cuXAxAcHMynn34K\ngMVi4dFHH6Vr166sWbOGHj16MHbs2OKtXkRExAEVOq0dHh5OaGgoACEhISQmJpKcnHzFel9++SV3\n33035cqVK/oqRUREypBCwzk2Npby5ctbH5vNZmJiYq5Y7/PPP6d3797Wx1u2bGHw4ME89thj7N+/\nv4jKFRERcXzXfflOI58b0O/cuZPatWvj7e0NQLNmzTCbzXTu3JmdO3cyduxYvvnmmwL3W768Fy4u\ntr2dX2Cgj01fv7g5en/g+D2qv9LN0fsDx++xpPorNJyDgoKIjY21Po6OjiYwMDDPOhs2bKBdu3bW\nxyEhIYSEhADQvHlz4uPjyc7OxrmAm0/YOphFRETsRaHT2h06dGDNmjUA7Nu3j6CgIOsI+aK9e/fS\noEED6+OFCxfy7bffAnDo0CHMZnOBwSwiIiL/KHTk3KJFCxo3bkzfvn0xmUxMnjyZlStX4uPjQ7du\n3QCIiYkhIOCfu0D16tWLF198kWXLlmGxWJg2bVrxdSAiIuJgTEZ+B5FFRETEZnSFMBERETujcBYR\nEbEzCmcRERE7c92fcy5NrnZNcIDFixezatUqnJycaNKkCRMmTMBisTBhwgSOHz9OdnY2Y8aMoWXL\nljz66KOkpqbi5eUFwNixY2nSpImt2rK63v5WrlyZ7zXPDxw4wJQpUwCoX78+L7/8si3aucL19vfe\ne++xceNGAHJycoiNjWXNmjV07dqVihUrWj8xMGfOHIKDg23S0+UK6nHdunW89957uLm50bNnT/r3\n73/VbU6fPs2YMWPIzs4mMDCQ1157DTc3N1u1ZXUj/c2ePZvt27djsVh48sknueuuuxg3bhz79u3D\n398fgMGDB9O5c2dbtJTH9fa3efNmnnnmGerWrQtAvXr1mDhxosO8f59//jmrVq2yrhMREcHOnTvt\n9nco5H6iaMSIEQwcOND6f/CijRs3Mm/ePJydnenYsSMjR44ESuhn0HBQmzdvNoYOHWoYhmEcPnzY\n6NOnj3VZUlKS0aVLFyMrK8swDMN4/PHHjZ07dxorVqwwJk+ebBiGYRw6dMh46KGHDMMwjP79+xsH\nDx4s2QYKcSP9ffHFF8bMmTOv2Ff//v2N3bt3G4ZhGM8//7yxYcOGEuigYDfS36VWrlxpLFy40DAM\nw+jSpYuRnJxcQpVfu4J6zM7ONjp27GjExcUZ2dnZxqBBg4zTp09fdZtx48YZ33//vWEYhjF37lxj\n8eLFJdzNlW6kv/DwcGPIkCGGYRhGfHy80alTJ8MwDGPs2LHGzz//XOI9FORG+tu0aZPx1FNPXbEv\nR3n/Lt9+ypQphmHY5+9QwzCMlJQUo3///sZLL71kfPrpp1cs7969uxEVFWVkZ2cb/fr1M/76668S\n+xl02Gntgq4J7urqiqurK6mpqVgsFtLS0vDz8+O+++5j/PjxQO5lSs+dO2ez+gtzI/3lJzMzk1On\nTln/Iu7SpQvh4eEl00QBbqY/i8XC0qVLr/gr2N4U1GNCQgK+vr6YzWacnJxo27YtGzduvOo2mzdv\n5s477wRKx3t4tf5atWrFm2++CYCvry9paWlkZ2fbrIeC3Eh/V+Mo79+l3nnnHUaMGFHidV8PNzc3\nFi5cSFBQ0BXLTpw4gZ+fH5UqVcLJyYlOnToRHh5eYj+DDhvOBV0T3N3dnZEjRxIaGkqXLl1o1qwZ\ntWrVwtXVFXd3dwA++eQT7r33Xuv2b731Fo888giTJk0iPT29ZJvJx430B1de8/ziD9lFAQEB+V47\nvaTdaH8Aa9eu5fbbb8fDw8P63OTJk+nXrx9z5szJ9xK0tlBQj2azmZSUFI4ePUpWVhabN28mNjb2\nqtukpaVZp9BKw3t4tf6cnZ2tU58rVqygY8eO1sMRn332GQMGDOC5554jPj6+5Bu6zI30B3D48GGG\nDRtGv379+OOPPwAc5v27aM+ePVSqVCnP1STt7XcogIuLS57fE5eKiYnBbDZbH1/sv6R+Bh36mPOl\nLv2FnJyczIIFC1i9ejXe3t489thjHDhwwHqVs8WLF7Nv3z7ef/99AAYMGED9+vWpXr06kydPZvHi\nxQwePNgmfVzNtfSX3zXPP/zww6vux55cz/v3xRdf5Dlu/vTTT3PHHXfg5+fHyJEjWbNmDffcc0+J\n91CYS3s0mUzMnDmTsLAwfHx8qFq1aqHbFPScPbie/tatW8eKFSv46KOPALj//vvx9/enYcOGfPDB\nB7z99ttMmjSpROsvzLX0V7NmTUaNGkX37t05ceIEAwYMYO3atVfdjz25nvdvxYoV/Otf/7I+Lg2/\nQ29Ucf0MOuzIuaBrgkdGRlKtWjXMZjNubm60bNmSiIgIIPfuWj///DPvvvsurq6uAHTr1s16ElXX\nrl05dOhQCXdzpRvpLyQkxHoSzcVrnpcvXz7P9P3Zs2fzneIpaTf6/qWmpnLmzJk8vyweeOABAgIC\ncHFxoWPHjnbx/kHh161v3bo1S5YsYcGCBfj4+FClSpWrbuPl5WUdjZSG9xDy7w/gt99+4/3332fh\nwoX4+OTeZKBdu3Y0bNgQKB0/g5B/f8HBwfTo0QOTyUT16tWpUKECZ8+edaj3D3Kn6Zs3b259bI+/\nQwtzef8X35eS+hl02HAu6JrgVapUITIy0vqNjIiIoGbNmpw4cYJly5bx9ttvW6e3DcNg4MCBnD9/\nHsj9T3fxTEtbupH+8rvmuZubG7Vr12bbtm1A7pTwHXfcYYOO8rqR/gAOHDhA7dq1rftJSkpi8ODB\nZGZmArB161a7eP+g8OvWDxkyhLi4OFJTU1m/fj3t2rW76jbt27e3Pl8a3kPIv7+kpCRmz57NggUL\nrGdmAzz11FOcOHECKB0/g5B/f6tWrWLRokVA7rRpXFwcwcHBDvP+QW4wlStXzjrFa6+/QwtTtWpV\nkpOTOXnyJBaLhfXr19OhQ4cS+xl06Mt3zpkzh23btlmvCb5//37rNcGXLVvGypUrcXZ2pnnz5owZ\nM4Z58+bx3XffUblyZes+Fi1axLp16/jwww/x9PQkODiYadOm4enpacPOcl1vf2fOnOHFF1/EMAws\nFov1IwCHDx9m0qRJ5OTk0KxZM+tJcbZ2vf0BrFmzho0bN+aZ1v7kk0/46quvcHd3p1GjRkycOBGT\nyWSrtvIoqMe1a9fyzgabUIsAAADuSURBVDvvYDKZGDRoEPfdd1++2zRo0IDo6GjGjh1LRkYGlStX\nZsaMGdaZH1u63v6WL1/O/Pnz85xDMGvWLI4fP85rr72Gp6cnXl5ezJgxI8/1/G3levtLTk5m9OjR\nnD9/nqysLEaNGkWnTp0c5v2D3D+W33jjjTyHzL7//nu7/B0aERHBrFmzOHXqFC4uLgQHB9O1a1eq\nVq1Kt27d2Lp1K3PmzAHgrrvusk7Fl8TPoEOHs4iISGnksNPaIiIipZXCWURExM4onEVEROyMwllE\nRMTOKJxFRETsjMJZRETEziicRURE7IzCWURExM78P0Sk3NpzvRYpAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 721
+ },
+ "outputId": "88bc0cb2-f6c5-40a1-9dea-5c67cfa3a36c"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000)"
+ ],
+ "execution_count": 31,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.087256104\n",
+ "Loss after epoch 50 is 0.087244704\n",
+ "Loss after epoch 100 is 0.087233305\n",
+ "Loss after epoch 150 is 0.08722193\n",
+ "Loss after epoch 200 is 0.08721054\n",
+ "Loss after epoch 250 is 0.087199144\n",
+ "Loss after epoch 300 is 0.08718776\n",
+ "Loss after epoch 350 is 0.08717637\n",
+ "Loss after epoch 400 is 0.08716498\n",
+ "Loss after epoch 450 is 0.0871536\n",
+ "Loss after epoch 500 is 0.087142214\n",
+ "Loss after epoch 550 is 0.08713083\n",
+ "Loss after epoch 600 is 0.087119445\n",
+ "Loss after epoch 650 is 0.08710805\n",
+ "Loss after epoch 700 is 0.08709667\n",
+ "Loss after epoch 750 is 0.0870853\n",
+ "Loss after epoch 800 is 0.08707392\n",
+ "Loss after epoch 850 is 0.08706254\n",
+ "Loss after epoch 900 is 0.08705116\n",
+ "Loss after epoch 950 is 0.087039776\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.027285745\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xlc1PXa//HXMMOACAKjgAuSijuG\nS+ZGuYKWVqdO3WalbZaZ2nayNMq0LFNPeU7abutdVty/snPs1BHFNEsRM5cENQU3XAFZFJFt+P7+\nGBs1FVyAgeH9fDx85Mx3ZrguSd5+t89lMgzDQERERGoMD1cXICIiImdSOIuIiNQwCmcREZEaRuEs\nIiJSwyicRUREahiFs4iISA1jcXUBf8jMPObSrx8Y6ENOToFLa6hK7t4fuH+P6q92c/f+wP17rOz+\ngoL8zrtNe84nWSxmV5dQpdy9P3D/HtVf7ebu/YH791id/SmcRUREahiFs4iISA2jcBYREalhFM4i\nIiI1zAWF8/bt24mOjuazzz47a1tRURGTJk3ir3/9q/O5pKQkevXqxahRoxg1ahTTp0+vvIpFRETc\nXIW3UhUUFDB9+nR69+59zu2zZ8+mQ4cO7Nix44zne/Towdy5cyunShERkTqkwj1nq9XK/PnzCQ4O\nPuf2J554gujo6EovTEREpK6qcM/ZYrFgsZz/Zb6+vuTm5p71fGpqKmPHjiUvL48JEyYQFRVV7tcJ\nDPRx+T1yf74hfObMmaSkpJCZmcmJEycICwvD39+fN954o1K+3sCBA2ncuDFm86m+P/3008v+3GXL\nlnHttdeSl5fHvHnzePHFF4Hyb3h3F+7eo/qr3dy9P3D/HqurvypZIaxFixZMmDCB66+/nvT0dO6+\n+26WLFmC1Wo973tcvapMUJDfWauUjR49HoDvv/+WnTvTmDDhcaDyVjOz28t45ZV/4OPj43yuMj77\nvffep3XrTvj4+PDII0+RmXnsnP25G3fvUf3Vbu7eH7h/j5XdX3lBXyXhHBISwtChQwEICwujUaNG\nHD58mObNm1fFl6t269ev48svP6OgoIAJE57gyScn8N13ywB47rmn+etfh9O+fQdmzHiBY8eOYbfb\nefzxp2jdus0Fff6wYYPO+rwNG37l+PF89u7dw/79+3j00Sfp3TuKxYu/46uv4jCZTIwYcRclJSVs\n2ZLMxImPMnnyFF544Tk++OBTkpKSmD37VSwWC0FBwTzzzPMkJMTz228byc3NYe/ePdx55yhuuOHm\nKvtzExGRC1Ml4bxo0SIyMzMZPXo0mZmZHDlyhJCQkMv6zGmrn+PbtH9VUoUON4bfzLQ+L13Se9PS\nUvnii4XnPRrwf//3BT179uHGG29m166dvP76q/zzn29dTrlkZBzm1VfnsmbNav7976/p3LkLH3/8\nPp988gXFxSW8/PJUZs6cw/vvv8Orr84lL+/U6YapU6fy6qvzCAlpzJw5s1i6dDEmk4m0tFTeeedD\n9u1LZ+rUWIWziMifmA4fxrpyOfS5GpqFV8vXrDCck5OTmTVrFvv378disRAfH8/AgQMJDQ0lJiaG\nRx99lEOHDrFr1y5GjRrF8OHDGThwIBMnTmTZsmWUlJQwbdq0cg9p10atW7cpt6fNm38jNzeH+Pjv\nASgqKjzn6yZOfBQPD8d1eQEBgbz00qzzfmZkZBcAgoODyc/PZ/fuXYSFtcDLyxsvL29mzpxzzvcd\nPZqHyWQiJKQxAN26dWfjxvW0bdueTp0iMZvNBAUFc/x4fsWNi4i4u7IyLBt+xZqwBGvCEjw3bXA8\nf/318ElctZRQYTh36tSp3IuUzne71DvvvHPpVZ3DtD4vXfJeblXw9PQ85/OlpaUnt1t44omn6NQp\nstzPefXVuWeccz7f5wFnXDhmGAYeHmYMo+wCqjVhGIbzUUlJCSaTxzk/U0SkLjLl5mBd8QPWpfFY\nlyfgkZUFgOHpSfG1/SiOHoLvQ/dXWz01ZmRkbWYymSgsdOwZb9/+OwAdO3Zi5coVdOoUya5dO0lK\nWs2IESMv+fPO5YorWrB37x4KCgowm81MmvQE//jHm5hMHtjtdufrGjRogMlk4tChQzRu3JiNG9cT\nGdnljNeIiNQphoF5SwrWZSf3jn9JwnTyZ6I9pDEn7rqb4ughlPTth+HXAADfID+opgveFM6V4Oab\nb2PMmHto0aIV7dp1AOC2227n5ZenMW7cA5SVlfH44xMv6/POpV69eowePZbHHx8HwO2334nJZKJr\n126MGzeaZ5+d5nzt9OnTeeGFZzGbzTRrFsqgQYNZsuS/l9awiEhtlJ+P9eeVjr3jZUswH9gPgGEy\nUdqtO8UxQyiOGUJpp0gwmVxaqsmoIccyXX35vW4BqP3cvUf1V7u5e39QM3s070w9de549c+YiosB\nKAsMpHhANMXRgykeEI3RsGGFn1Xrb6USERFxiaIiPBNXYU2Ix5qwBMvONOemkk6RFMcMpnjQEEqv\n6g5m1y58VR6Fs4iI1GoeB/Y7946tK1dgKjgOQFl9X4qG3ujYOx4UQ1mTpi6u9MIpnEVEpHYpLcWy\n7he8li3BujQey5bkU5tat6F40GCKY4ZQ0rM3eHm5sNBLp3AWEZEaz5SVhfWHpY6rq5cvw+PkTAfD\ny4viAYMojh5MUfQQylq2cnGllUPhLCIiNU9ZGZbNm04ero7Hsv5XTCevX7Y3C+XEX251HK6+pi/U\nr+/iYiufwllERGoE09E8PH9c7gjkZUsxZxwGwDCbKenVx3m42t6+g8tvdapqCudyHDx4gLvvHkG7\ndu0BKC4u5q677qFfvwEX/Vlffx1Hbm4uffv2Z+XKFYwe/dA5X/fzzz/Ss2ef865AdrqdO1OZM2c2\nb7zx3hnP9+vXkyuv7Ox83LBhQ9566/LHXC5fnsCAAdHs2PF7uT2IiFwQw8C8/Xfn3rFnUiKmk6si\nljVqROHwOxz3HvcbgBEQ6OJiq5fCuQJhYVc4w+/o0Tzuu+8uevXqjZeX9yV9Xps27WjTpt15t3/5\n5QK6dbv6gsL5fHx9fc8K7Mrw2WefMGBAdIU9iIicV0EB1tU/nVwIZCnmvXucm0q6dKU4egjF0YMp\n7dINTs4dqIsUzhehQQN/GjZsxJEjR/joo/lYLJ4cPZrLiy/OZPbslzlwYD+lpaU88MBYrrrqatat\nW8vcua9hszWkYcNGNG3ajPXr17Fw4f/x0kuzyx33+Prrb7No0TckJCzGZPLg2mv7c8cdI8nIOMyU\nKZPx9PSkdeu2F1z7vn37GDduAh984FgnffToUbz00iw+/PA9GjUK4vfft3L48CGef/4l2rVrz4IF\nn7BixTJMJg/Gjp3Atm1bSE3dTmzsU9x22+3OHpYtW0pc3ALMZjPt2nXg8ccn8sEH755zvKWI1E0e\ne/c4V+Wy/rwS08nlicv8GlB40y2Oc8cDYzCCg11cac1Ra8K5/rTn8Pq2ckdGFt14M8enXfgwjYMH\nD3D0aB7BwY7xlw0aNGDSpGdZvPg7GjZsxDPPPE9ubi6PPTaWTz75knfffYMpU6bTpk1bJk58lKZN\nmzk/q6DgeLnjHjMzM1ixYhlvvfUBAA8/PJoBA6JZuDCOQYMGM3z4HXz22cekpm6/7D+H4uJi5sx5\ng3/96ysWL/4OHx8fVqxYxrvvfsyBA/v57LOPmTx5CgsWfMKMGX9n/fp1J3so4L333uSjjz7Hx8eH\np59+wrntz+MtFc4idUhJCZ5Jiacu5jptRkBp+w7OveOSq3vCZRwldGe1JpxdZe/ePUyYMAYAq9XK\nc8+9gMXi+GPr2DECgOTk39i0aQO//bYRgKKiIkpKSjh48CBt2jj2brt06UZRUZHzcysa97h1awr7\n9qXzyCOO87oFBcc5dOgAu3fvYsCAaAC6du3OmjWrz6o5Pz/fWTNAeHhrxo07//nhzp27AhAUFMKW\nLSls3/47HTt2wsPDg9DQ5kyePOWc70tP30toaJhzqlbXrlexffs24OzxliLi3kyHD8N/vqLBwn/j\n+eNyPI4dBcCoV4+iwdc5AnlQDGXNw1xcae1Qa8L5+LSXLmovt7Kcfs75zywWT+d/7777fmJirjtj\nu8dp50v+vIR5ReMeLRZPeveO4umnnz3j+QULPnGOezzf+891zrm4+OgZj8sbRWk2e1BWVvGS6ybT\nmX2VlpbgdfKGf42iFHFzdjuWjeud547/mHnsBdivaEHB7Xc49o77XAvel3aNTl1Wd8+2V6KOHTvx\n888/ApCTk827774JQKNGQezduxvDMNiw4dcz3nP6uMeioiIef3wchmE4xz22a9eB9et/pbCwEMMw\n+Oc/X6WoqJCwsCvYtm0LgPMQ8oXw9fUlJycbwzA4ciSLAwf2nfe17dp1YPPmTZSWlpKdfYRnnnFM\n1PpzYDdvfgX79u2l4ORSeRs2rKddu44XXJOI1C6m3By8vvkKv/FjaNipNYHXD6L+nNlYtiRTfG1/\nmDOH7NW/kr12E8dn/J2SgTEK5ktUa/aca7KBA6NZv/4Xxo69H7vdzv33Ow4pjxkzjueem0Tjxk2c\n56n/UNG4x3nz3mP48DsYP/5BPDw86Nu3P15e3vzP/9zBlCmTWblyOeHhbS64Rn9/f7p378EDD9xN\n69Ztyr3aukmTpgwZMpQJE8ZgGAYPPTQegLZt2/Hgg3fz8MOPOnsYP/4xnnzyEUwmDyIju9C5cxfW\nrUu6qD8/EamhTpt57LU0HssvSZjKHEfszjXzOCjID3sNm0pVW2lk5Ek1cdRZZXL3/sD9e1R/tVut\n6S8/H+tPP55cCORPM4+vutpx33H04HPOPK41PV4ijYwUEZFq45x5vDQez8RVZ8w8LvzrbY6LuS5w\n5rFUDoWziEhdU1SE5+qfHfcdL43Hsmunc1NJp0jHfcfRNX/msTtTOIuI1AEe+/dhXbYUa0I81pU/\nOmceGz71Kbr+Bsfh6lo289idKZxFRNzRHzOPE+KxJixxy5nH7kzhLCLiJsqdeTwwmqLowRQPGuw2\nM4/dmcJZRKS2+mPm8cl1q+vazGN3pnAWEalFHDOPVzjOHZ9r5vHJdavrwsxjd6ZwFhGpyQwD847t\nzr1jzzWrT5t5HHRq5nH/gRj+AS4uViqLwllEpKY5cQLrqpUnpzotOXPmcdduzou5Sjt3rdMzj92Z\nwllEpAY478zjBv6aeVwHKZxFRFyhuBjPtWtOXcx1+szjDh0de8eaeVxnKZxFRKqJx+FDjoVAlsY7\nZh7nO9ZpNnx8KBpyvSOQNfNYUDiLiFQdux3Lhl+xJiyBFQk0XL/+1KYrWlAw4k7HVKc+12i0opxB\n4SwiUolMOdlYV/zgOFy9PAGPI0ccGzw9Kb62P8UxjnWr7eGtdauTnNcFhfP27dsZN24c9957LyNH\njjxjW1FREc8//zw7duxg4cKFzudnzJjBpk2bMJlMxMbGEhkZWbmVi4jUBH/MPE6IxythyZkzjxs3\n4cTIeygeNBj/W28kr9DFtUqtUWE4FxQUMH36dHr37n3O7bNnz6ZDhw7s2LHD+dzatWvZs2cPcXFx\npKWlERsbS1xcXOVVLSLiSuebeezh4Zh5HD2Yough2DtdeWrv2M8PCt131rFUrgrD2Wq1Mn/+fObP\nn3/O7U888QS5ubksWrTI+VxiYiLR0dEAhIeHk5eXR35+Pr6+vpVUtohI9TLvTHUcqk5Yco6Zx//j\nWAhkwCAMm2Yey+WrMJwtFgsWy/lf5uvrS+7JxdX/kJWVRUREhPOxzWYjMzNT4SwitUdhIZ6JqxzL\nZCYs0cxjqVbVckGYcXIh9vIEBvpgsbj2f/CgID+Xfv2q5u79gfv3qP6qWHo6fP+941dCAhQUOJ73\n9YVbboGhQ+H66/Fs1gxP4GJHSbi8v2rg7j1WV39VEs7BwcFkZWU5H2dkZBAUFFTue3JyCqqilAsW\nFORHZqb7ng9y9/7A/XtUf1WgtBTPdWsd546XxmPZmnJqU3hrxxCJc808voQ63f37B+7fY2X3V17Q\nV0k4R0VFMW/ePEaMGEFKSgrBwcE6pC0iNYJz5nFCPNblP+CRp5nHUvNUGM7JycnMmjWL/fv3Y7FY\niI+PZ+DAgYSGhhITE8Ojjz7KoUOH2LVrF6NGjWL48OHceOONREREMGLECEwmE1OnTq2OXkREznb6\nzOOEeCwb1p+aeRzanBO3/DHzuB/4+Li4WBEHk3EhJ4SrgasPhehwTO3n7j2qvwvnmHm8/OStTn+a\nedyzt3Pd6uqceezu3z9w/x5r/WFtEZFqZRiYt/9+auZxUuKZM49H3EVR9GBK+g3QzGOpFRTOIlI7\nFRRgXf3TyUBe6px5bJhMlHbtRvHAGM08llpL4SwitYbHnt3OVbnOmnn8l7+emnlcwd0hIjWdwllE\naq6KZh5HD3HMPO7eQzOPxa0onEWkRrmgmcfRgykLbe7iSkWqjsJZRFzr5MxjVq8gYNF/8Pxt46lN\nLVpScMddFA8arJnHUqconEWk2plysrEuX+Y4f3zazGOLpyfFfQdQHO24mMveSjOPpW5SOItI1TMM\nzCnJWJctwWtpPJZ1a8+aeVzv1ps50rkHhq97r80sciEUziJSNfLzsa5c4biyOmEJ5oMHgNNmHscM\noWjQYOfM43pBfhhuvICFyMVQOItIpTGn7Tg5RGIJnmtOm3lss1F463DHrU6aeSxSIYWziFy68mYe\nX9nZce44egil3TTzWORiKJxF5KJ47N93aiGQlSswnZx5XFbfl6JhNzn2jgfFUNa4iYsrFam9FM4i\nUr7TZx4nLMGyJfnUpjZtHfcd/zHz2Gp1YaEi7kPhLCJnMWVlOfaMly05c+axtzdFg2JO7h0PpqxF\nSxdXKuKeFM4i4ph5/NvGk3vH55l5HDOE4qi+mnksUg0UziJ1lOloHp4rfsDr5Mxjj8wMAAyLhZI+\n15yaedyuvRYCEalmCmeRuuL0mccJ8XiuXXNq5nFQsGPmccwQSvr218xjERdTOIu4s4ICrKtWOi/m\nMqfvBU6beXxyqlNpZBfNPBapQRTOIm7GOfM4IR7rqp/Onnk8KIbiQYM181ikBlM4i9R25c48jnBc\nWR0zxDHz2KK/8iK1gf6mitRC5515XK+eZh6LuAGFs0htYLdDYiI+X33jWLd686ZTmzTzWMTtKJxF\naihTTjbWHxKcM4/JzqY+YGjmsYjbUziL1BQnZx57/TFE4k8zj3ngAfKiBlDSr79mHou4OYWziCuV\nN/O4ew+KowdTFD0Ee0QngoIbUKx5xyJ1gsJZpJpVOPM4ZgjF/Qdq5rFIHaZwFqlq5c08juxyauZx\n16s081hEAIWzSJVwzjxOiMf604+nZh77+jlmHscMoXhgtGYei8g5KZxFKsPpM4+XxmPZmnJqk2Ye\ni8hFUjiLXKLzzjz28tLMYxG5LApnkQtV0czjm2+lOGYwxdf008xjEbksCmeRcpiO5uH543K8lsZr\n5rGIVJsLCuft27czbtw47r33XkaOHHnGttWrVzNnzhzMZjN9+/Zl/PjxJCUl8dhjj9GmTRsA2rZt\ny5QpUyq/epHKZhiYf9/m3Ds+Y+Zxo6BTM4/7DcBo4O/iYkXEXVUYzgUFBUyfPp3evXufc/tLL73E\nBx98QEhICCNHjmTIkCEA9OjRg7lz51ZutSJVoaAA688/OgJ52VLNPBYRl6swnK1WK/Pnz2f+/Pln\nbUtPT8ff358mTRy3g/Tr14/ExETatm1b+ZWKVCKP3buwLluC19J4PFf9hKmoCIAy/wAKb/6r43D1\nwBjNPBYRl6gwnC0WC5bzzIDNzMzEZrM5H9tsNtLT02nbti2pqamMHTuWvLw8JkyYQFRUVOVVLXKx\niovxTEo8NfN4x3bnptIOEY77jqMHa+axiNQIVfJTqEWLFkyYMIHrr7+e9PR07r77bpYsWYK1nPs7\nAwN9sFhcuzpSUJB7DxNw9/7gTz0ePAjff+/4tXQpHDu5LrWPD9x0EwwdCkOHYmneHAtQG66vdvfv\nofqr/dy9x+rq77LCOTg4mKysLOfjw4cPExwcTEhICEOHDgUgLCyMRo0acfjwYZo3P//g95ycgssp\n5bIFBfmR6cZDBdy9P4Agmw858ctPLpO59KyZx0W330lx9JCzZx7Xkj8Xd/8eqr/az917rOz+ygv6\nywrn0NBQ8vPz2bdvH40bN2b58uW8+uqrLFq0iMzMTEaPHk1mZiZHjhwhJCTkcr6UyDmZso9gXb4M\na8ISWLGMwCNHgNNmHsecvNUpvI2LKxURuXAVhnNycjKzZs1i//79WCwW4uPjGThwIKGhocTExDBt\n2jSefPJJAIYOHUrLli0JCgpi4sSJLFu2jJKSEqZNm1buIW2RC2YYmJM3n5p5/OsvzpnHNGvGiVH3\nUjxoMCV9+2nmsYjUWibDOLnEkYu5+lCIDsfUXKb8Y3j+eNrM40MHgT/NPB40GNuAPmRm5bu42qpT\nm7+HF0L91X7u3mOtOawtUiUMA3NaquPc8R8zj0tKgJMzj2+73bFu9Z9nHmuFLhFxEwpnqRkKC/Fc\n/TPWhHi8EpZg3r3LuUkzj0WkrlE4i8t47Es/uSrXkvPPPB4UQ1lIYxdXKiJSvRTOUn1KS/H8JenU\nVKetW05tat3GsUymZh6LiCicpWqZMjOx/rDUEcjLl+FxNA8Aw9tbM49FRM5D4SyVq6wMy6YNzsPV\nZ808/uttjsPVUX0181hE5DwUznLZTHm5WFf84Jzq5JGVCZw283hgDMUxQzTzWETkAimc5eIZBuZt\nW8+ceWy3A1AWFKyZxyIil0nhLBfmj5nHSx2Hq8370gHNPBYRqQoKZzkvj927nPcda+axiEj1UTjL\nKcXFeK5ZfepWp9Qdzk2lHTs5rqzWzGMRkSqnn7B1nMfhQ44wXhqP54/L8TjuWJva8PGh6LqhjsPV\ng2Ioaxbq4kpFROoOhXNdY7djWb/unDOPS1u2ojBmlGOqU++oM2cei4hItVE41wGmnGxY+i1+C/+N\ndXkCHtnZABhW66mZxzFDsLdq7eJKRUQEFM7uyTAwpySfmnm8bi2UleEN2Js0dcw8jh5C8bX9wNfX\n1dWKiMifKJzdhCn/GJ4rfzx5uPrsmceeN99Edq9+2CM6aSEQEZEaTuFcWxkG5p2pWJeePHec+PO5\nZx4PGIQRaCMoyA+7Gw9BFxFxJwrn2kQzj0VE6gSFcw1X7szjG/5C8aAYx61OjZu4uFIREaksCuea\npqQEz3VrHYerly05c+Zx23bOZTJLevTSzGMRETelcK4BTJmZjj3jZUvPM/PYEchlV7RwbaEiIlIt\nFM6ucPrM44R4LBs3nJp53DyME7f+j2PmcZ9rNfNYRKQOUjhXkwpnHp/cO7a3badbnURE6jiFc1Wp\nYObxiTtGOs4da+axiIj8icK5Mh0/jvXnlc6rq8+YedztqlMzj6/srJnHIiJyXgrny+SxayfWZUvw\nWhqP5+qfz5x5fMutp2YeN2rk4kpFRKS2UDhfrD9mHv9xq5NmHouISCVTelwAj0MHT547XqKZxyIi\nUuUUzudit2P5dR3WZfFYly7BM/k35ybNPBYRkaqmcP7DkSN4ff0vx+Hq5Ql45OQAJ2ce9xvgOFyt\nmcciIlIN6m44Gwbm5M3Omcf8+gsNysqAP2Ye/8VxMVff/pp5LCIi1apOhbMp/xieP65wLJX5p5nH\n9OlDfr9BFEcPwd4xQguBiIiIy1xQOG/fvp1x48Zx7733MnLkyDO2rV69mjlz5mA2m+nbty/jx48H\nYMaMGWzatAmTyURsbCyRkZGVX31FDANz2h8zj5fguWbV2TOPY4ZQ3H8gjdpewQnNOxYRkRqgwnAu\nKChg+vTp9O7d+5zbX3rpJT744ANCQkIYOXIkQ4YMITs7mz179hAXF0daWhqxsbHExcVVevHnY07b\nQb3333XsHe/Z7Xy+pHNXx4jFmCGUdummmcciIlIjVRjOVquV+fPnM3/+/LO2paen4+/vT5MmjlnC\n/fr1IzExkezsbKKjowEIDw8nLy+P/Px8fKvp3K3PKy/hvegbyvwaUHTjzRRFD6ZkYDRlIY2r5euL\niIhcjgrD2WKxYDnPYhqZmZnYbDbnY5vNRnp6Ojk5OURERJzxfGZmZrWFc/7LszkxZhylXbuBp2e1\nfE0REXFPP+37kbnr59A/vC/jI56slq9ZLReEGSfHIZYnMNAHi6WSDjMH+UGni7/lKSjIr3K+fg3l\n7v2B+/eo/mo3d+8P3KvHVXtXMWX5FJbvXg5A31bXVFt/lxXOwcHBZGVlOR8fPnyY4OBgPD09z3g+\nIyODoKCgcj8rJ6fgckq5bEFBfmS68QVh7t4fuH+P6q92c/f+wH163JSxgZlrX2LZ3qUADAqLYXKP\n54iO6Fup/ZUX9Jc1Gik0NJT8/Hz27dtHaWkpy5cvJyoqiqioKOLj4wFISUkhODi42g5pi4iIXIqt\nR7Zw73/vIuarfizbu5Soptfy7S1L+OKGr+kc3LVaa6lwzzk5OZlZs2axf/9+LBYL8fHxDBw4kNDQ\nUGJiYpg2bRpPPuk4Bj906FBatmxJy5YtiYiIYMSIEZhMJqZOnVrljYiIiPxZctZm3t30JsvTl+Hp\n4Ym3xZt6Fh+8zd7U8/TBx1IPb3M9jpfks2zvUgwMrgq5mtiez3NtaD+X1W0yLuSEcDVw9aEQdzkc\ncz7u3h+4f4/qr3Zz9/6g5vRYZpSxZPdi3vvtLX7evxKAEJ/GeJm9OFF64uSvAuyG/Yz3XdmoM8/0\nfI5BYYMxnWMhqsrur7zD2nVqhTAREXFf+SX5xG1bwHu/vc2uvJ0A9A0dwEORDzPoisF4mM48k1ti\nL+FEaQEn7IWU2kto6tvsnKHsCgpnERGp1fYdS+f9ze/y2ZZPOFqch5fZizvbj2JM53F0bBhx3vd5\nmj3xNPvTAP9qrPbCKJxFRKRW2pz1G29tmMu/Ur/GbtgJqhfM01fHck/EaIJ8yr9DqKZTOIuISK1h\nGAYr0n/gzY1zWbnPcf9xB1tHHu7yCLe0uQ0vs5eLK6wcCmcREanxSuwlfJP6FW9tnMeWI8kAXNOs\nL+O7PMrAsJgac664siicRUSkxiqyF/Fx8vu8vfENDhzfj9lk5pbWtzKuy6PVfu9xdVI4i4hIjWMY\nBot3f8/UVbHsProLH0t9Hryk7IVPAAAgAElEQVRyLA91Hk9YgytcXV6VUziLiEiNsvXIFqaseoaV\n+5Zj8bAwJvJh/tb9aWzeDV1dWrVROIuISI2QXXiE2Wtn8EnKh9gNOwPDonmxzyu0tbVzdWnVTuEs\nIiIuVWIv4eOU9/n7L6+QW5RLeEBrpke9QvQVQ1xdmssonEVEpFrlFx9jW/ZWtmVvZeuRFJanLyM1\ndwcNrP68GDWD+zuNwWq2urpMl1I4i4hIlcksyGTlvuXOIN6WvZW9x/ac8RqzyczdHe9ncs/naFSv\nkYsqrVkUziIiUqkMw2D1gZ/5JOUDvtv5LSVlJc5tQfWCuTa0Px1tHWlv60j7hh1oZ+uAr6fGCp9O\n4SwiIpUi+0Q27256j09SPiQ1dwcA7W0dGN7uTroEd6W9raP2jC+QwllERC6ZYRj8evgXPkn5kH+n\nLaSwtBCrh5Vb2wznnk6j6dm4l9ut3lUdFM4iInLRsk5k8fX2OL7YtsC5nGZrW2vuancvI9rfRcN6\ndeee5KqgcBYRkQtSWlbKD3uX8sW2BSzZ/V9KykqweFi4odVfuCfifv7a9QaOZB13dZluQeEsIiLl\n2pGznS+2fcb//f4FGQWHAehgi+DODiO5te3tzvPIHiYPV5bpVhTOIiJyFsMwWLpnMXPX/4O1h9YA\n4O8VwP2dHuSO9iOJDOqic8lVSOEsIiJOhmHw313f8dq6WWzO2gRA/+YDubP9KK5rOQxvi7eLK6wb\nFM4iIkKZUcZ3O79lzrrZpBzZjAkTt7S+lceveooODTu6urw6R+EsIlKH2cvs/Gfnv5mzbjZbs7fg\nYfLg1jbDeeKqp+rkwImaQuEsIlIH/XH4ekbSC2zP+R2zyczwdnfweLeJtA5s4+ry6jyFs4hIHfNb\n5kamrnqWVQd+wmwyc0f7kTx21ZO08g93dWlyksJZRKSOOHT8IDOSXiRu2+cYGAxpcT1Te7+kPeUa\nSOEsIuLmCkoKeGvjXN7Y8E8KSgvo2LATL0bNoG9of1eXJuehcBYRcVNlRhlfbY/j5TUvcPD4AYLq\nBfPyNbMZ0f4uzB5mV5cn5VA4i4i4geMlx/k9eytbj2xhy5FktmY7/ptdmI2X2YvHu03k0W5P4Gv1\nc3WpcgEUziIitUSRvYj9+fvYdyyd9KN7ST+2h99zfmfLkWR25+3CwHC+1oSJKxq04LoWw3jy6kk0\n9wtzYeVysRTOIiI1UNaJLD7c/B4781LZe3Qv+/LTOXz80BkB/IdAr0D6NL2GDg070rFhJzo07Eg7\nWwd8PX1dULlUBoWziEgNk7Annsd+GE/miQwAzCYzzXxD6dP0GkL9mtPcL4zmfmGE+jWnTWBbQnwa\na51rN6NwFhGpIQpKCngh8Tk+Sn4fTw9PpvR+kVta30rj+k2weOjHdV2i77aISA2wMWM94xIeJDV3\nB+1tHXgr+n06NbrS1WWJi1xQOM+YMYNNmzZhMpmIjY0lMjLSuS0hIYG3334bq9XKsGHDGDlyJElJ\nSTz22GO0aeO4sb1t27ZMmTKlajoQEanFSstKmbf+H/x93SuUlpXyUOQ4nu01TdOf6rgKw3nt2rXs\n2bOHuLg40tLSiI2NJS4uDoCysjKmT5/ON998Q0BAAA8++CDR0dEA9OjRg7lz51Zt9SIitdjuvF2M\nXzaGXw4l0aR+U+YOfJt+zQe4uiypASoM58TERGfghoeHk5eXR35+Pr6+vuTk5NCgQQNsNhsAvXr1\nYvXq1TRr1qxqqxYRqcV+z97GNzv+H+/+9jbHS/L5S/hfmd1vDoHeNleXJjVEheGclZVFRESE87HN\nZiMzMxNfX19sNhvHjx9n9+7dNGvWjKSkJHr06EGzZs1ITU1l7Nix5OXlMWHCBKKiosr9OoGBPlgs\nrl2xJijIvW/Od/f+wP17VH+1V1p2GnHb4vgy+Us2Z2wGwN/Ln09v+ZS7rrzLba62dufvIVRffxd9\nQZhhnHaTu8nEzJkziY2Nxc/Pj9DQUABatGjBhAkTuP7660lPT+fuu+9myZIlWK3W835uTk7BJZRf\neYKC/MjMPObSGqqSu/cH7t+j+qt9DuTv59+p3/Cv1K/YkLEeAKuHletaDuOW1rcS0+I6fD19ycrK\nd3GllcMdv4enq+z+ygv6CsM5ODiYrKws5+OMjAyCgoKcj3v06MHnn38OwGuvvUazZs0ICQlh6NCh\nAISFhdGoUSMOHz5M8+bNL7kJEZGayF5m58Dx/ezK28nuvF2O/x7dxc7cNLZmpwCO+5SHhA9h2BU3\nc33LYfh7Bbi4aqnpKgznqKgo5s2bx4gRI0hJSSE4OBhf31OrzjzwwAPMmjWLevXqsXz5cu677z4W\nLVpEZmYmo0ePJjMzkyNHjhASElKljYiIVBV7mZ19+enszE1jZ14au/LS2Jmbxu6ju9h7dA/FZcVn\nvcfHUp8+Ta/h5ta3ckP4X+gQ1tKt9yqlclUYzt26dSMiIoIRI0ZgMpmYOnUqCxcuxM/Pj5iYGIYP\nH87999+PyWRizJgx2Gw2Bg4cyMSJE1m2bBklJSVMmzat3EPaIiI1yb5j6Xyw+T1Sc7ezMzeNPUd3\nnzOAbd42OjW6khb+rWjh35KWDVo5fx9cL9htziNL9TMZp59EdiFX/4tS50pqP3fvUf1Vj7UHk7h3\n8Z1kncgEIMArgFb+4bT0D6dVQDit/E/+Cgi/qMPTNaW/quTuPdaoc84iInVF3LbPeXLFo9gNOy9F\nzeS2drdj827o6rKkDlI4i0idZy+zMyPpReZt+Af+XgHMH/wx/ZsPdHVZUocpnEWkTssvPsa4hAdZ\nvPt7WvmHs2DY/xEe0MbVZUkdp3AWkTor/dheRn53O1uzU+gbOoD3B39MgHegq8sSwcPVBYiIuELS\nwTUM+ao/W7NTuL/Tg3wx7CsFs9QY2nMWEbdnGAYZBYdJzd1Bau4Ofs/eyv+mfITdsDOr7xzu6/SA\nq0sUOYPCWUTczk/7fiTpYCKpuTtIy00lLTeV/JIzb4EJ9Apk/pBP6Bva3zVFipRD4SwibiPrRBax\nP03kX6kLnc95mb1o6d+K8IA2tA5oQ3hAa1oHtKF9w474evqW82kirqNwFhG3sCj1Gyb/9CRZJ7Lo\nHtKDJ66aSJvAdjT3C8Ps4dqJdyIXS+EsIrVaRkEGk1c+yX92/htvszcv9JnBmMiHFchSqymcRaRG\nySjIYP3hdScPRbfG4nHuH1OGYfCv1K955qeJZBdm07NJb14f8CatAlpXc8UilU/hLCI1Qom9hHc2\nvcHsta84L97yMnvRJrAdHRtG0MEWQceGjl+YTEz68W98v+tb6lnq8fI1sxh95UN4mHR3qLgHhbOI\nuNzP+1cy5f9NIiUzhQCvAB7r9iQZBYfZciSF37O3kpz12xmv9zB5UGaU0btpFP8Y8Aat/MNdVLlI\n1VA4i4jLHMjfz7TVz/Kv1IWYMDGq433E9nyehvVODZuwl9nZfXQnW46kOH8dyN/PiPZ3cl+nB7W3\nLG5J4Swi1a7IXsS7m95kzrrZFJQWcFVId9656W2u8Gx31mvNHmbCA9oQHtCGG8NvdkG1ItVP4Swi\n1cZeZmfJnsW8mDiFtNxUGtVrxIxr/86I9ncREuzv1rOARS6GwllEqlxuYQ6fb/uMj5Lns+fobjxM\nHjxw5UM8fXWs1rMWOQeFs4hUmZSsZD5Mfo+vtsdxovQE9Sz1GNXxXh6MfJj2tg6uLk+kxlI4i0il\nKrGXsHj3d7y/+V0SD6wCIMzvCu7r9CB3dhhJoLfNxRWK1HwKZxGpFIWlhSzY+r+8seGf7M/fB0C/\n0AE8EDmW6LDBWrFL5CIonEXksjhC+RNeXz+HQ8cPUs9Sj9FXjuH+TmNoE9jW1eWJ1EoKZxG5JIWl\nhXy25WPmbvgHh44fxMfiw/gujzGuy6ME+QS5ujyRWk3hLCIX5UTpCT5N+Yh5G/7J4YJD+FjqM6Hr\n44zr8iiN6jVydXkibkHhLCIXpNhezKdbPuIfv75KRsFh6nv68mjXv/Fwl0fOWNFLRC6fwllEymUv\ns/PV9jj+/ssr7D22h/qevjzW7UnGdp6gUBapIgpnETknwzD4767vmLl2Otuyt2L1sPJQ5Dgeu2qi\nDl+LVDGFs4ic5ad9PzIj6QV+PbwOD5MHd7YfxcSrJxPq19zVpYnUCQpnEQHgcMFh1h1ay0fJ77Ny\n33IAbgy/mck9ntMtUSLVTOEsUgcV24vZnLWJXw/9wq+Hf2Hd4V9IP7bXub1f6ACe7TWVLsHdXFil\nSN2lcBapAwzDYH3GOr7f+R8SD6xic9YmiuxFzu0NvRsy+IrruCrkaq4N7Uf3xj1cWK2IKJxF3JS9\nzM7aQ2v4T9q/+W7ntxw4vh8As8lMp0aRXBXSnatCruaqxlfTskErTCaTiysWkT8onEXcSIm9hJ/3\nr+S7nd/y/a5vyTqRCYC/VwC3t7uTYa1u4trQftT3rO/iSkWkPBcUzjNmzGDTpk2YTCZiY2OJjIx0\nbktISODtt9/GarUybNgwRo4cWeF7RKTyHC44zPK9Cfywdykr0n8gtygXgEb1ghjV8T5uaHUT1zTr\ni6fZ08WVisiFqjCc165dy549e4iLiyMtLY3Y2Fji4uIAKCsrY/r06XzzzTcEBATw4IMPEh0dzd69\ne8/7HhG5PKVlpaw7tJZle5fyw94ENmdtcm4L9W3ObW1v54ZWf6Fnk96aBCVSS1UYzomJiURHRwMQ\nHh5OXl4e+fn5+Pr6kpOTQ4MGDbDZHPNZe/XqxerVq0lPTz/ve0Tk4hmGQXxqPG+ueYcf05dztDgP\nAKuHlb6hAxgUFsOgsBjaBLbVuWMRN1BhOGdlZREREeF8bLPZyMzMxNfXF5vNxvHjx9m9ezfNmjUj\nKSmJHj16lPue8wkM9MFice2/8oOC/Fz69auau/cH7tejYRgs3bmUaSumkbgvEYCWAS0ZGXkX17W+\njgEtB+BrdZ9/9Lrb9+/P3L0/cP8eq6u/i74gzDAM5+9NJhMzZ84kNjYWPz8/QkNDK3zP+eTkFFxs\nKZUqKMiPzMxjLq2hKrl7f+BePRqGwcp9K5j9ywx+OZQEwM3tb2Z8pyeIDOri3Ds+kWdwAvfo2Z2+\nf+fi7v2B+/dY2f2VF/QVhnNwcDBZWVnOxxkZGQQFnZrV2qNHDz7//HMAXnvtNZo1a0ZRUVG57xGp\nizZnbuJ4aQFN6zelcf0mWM3Ws15jGAY/7f+Rv//yCkkHHXvK17UYylNXP8PAjte49Q8+ETmlwnCO\niopi3rx5jBgxgpSUFIKDg884PP3AAw8wa9Ys6tWrx/Lly7nvvvto0qRJue8RqUsKSgqYsmoyn275\n+IznG9ULokn9pjT1bUrj+k1pUr8JP+5bTuKBVQAMaXE9E7tPpnNwVxdULSKuVGE4d+vWjYiICEaM\nGIHJZGLq1KksXLgQPz8/YmJiGD58OPfffz8mk4kxY8Zgs9mw2WxnvUekLtp6ZAtjltzL7znbiGh4\nJQPDojl4/ACHjh/kQP5+0nJ3nHG1NUDMFUN46upntHSmSB1mMi7khHA1cPXhOp0rqf1qUo+GYfBJ\nyoc8v+oZCu2FPHDlQzzfezreFu+zXpdXlMvB4wc5eHw/IT5NiGjU6ZyfWZP6qwrqr/Zz9x5r1Dln\nEbk4uYU5PLHiEb7buYhAr0DeG/wx17Uces7XmkwmArwDCfAOpEPDjtVcqYjUVApnkUqUdHANDy8d\nzb78dHo3jeLt6Pdp6tvM1WWJSC2jcBapBCX2Et7Y8E9m/zIDA4Onr47liaue0gpdInJJFM4ilyHr\nRBafpnzERynvc+j4QZrWb8Y7MR/Qq2kfV5cmIrWYwlnkEmzO3MT8ze/wzY6vKLIX4evpx5jIh3my\n+yQCvW2uLk9EajmFs8gFKi0r5fud3zJ/8zvOBULCA1rzwJUPcXu7O/G1uveyhSJSfRTOIhVIP7aX\nuG2f89mWTzhwfD8Ag8JieDByLP2bD8LD5OHiCkXE3SicRc6hoKSA73Yu4sttC/hp/48A1Pf0ZfSV\nY3jgyocID2jj4gpFxJ0pnEVOMgyDtYeSiNu2gH+lLiS/xLHYQK8mfbij/UhuDP+LDl2LSLVQOEud\nV1hayIfJ8/nflA/ZmZcGQKhvc8Z0fpjh7e6glX+4iysUkbpG4Sx1lmEYxO/+L1NWTWbP0d14m725\ntc1w7ugwkmua9dW5ZBFxGYWz1Enbs3/nuVWTWJH+AxYPCw9FjuPJ7pMI8A50dWkiIgpnqVvyinJ5\n9ZeZfJD8HqVlpfRvPpCXombR1tbO1aWJiDgpnKXWyyzIZNX+lTTLDcZcVI9Abxs2bxsNrP6YTCYA\n7GV2Pt/2Ka8kvUjWiSxaNGjJi1GvMKTF9c7XiIjUFApnqbWOFR/lrY3zeHvjGxSUHj9ru8XDQoBX\nIDZvG8X2YnYf3YWPpT7P9ZrGQ53H42X2ckHVIiIVUzhLrVNkL+Lj5Pf556+vcqTwCEH1gnm02xP4\n+9Vnb9YBcoqyySnM5siJI+QUZZN1IpP84nxua3s7z/d+kcb1m7i6BRGRcimcpdawl9n5anscs3+Z\nQfqxvfhZGzC5x3OM6TwOX0/fcgehG4ahw9ciUmsonKXGMwyDpXsW8/KaF9iavQWrh5WxnSfwWLcn\naViv4QV9hoJZRGoThbPUWIcLDvOvHV/xf79/yeasTXiYPLij/UieuvoZQv2au7o8EZEqo3CWGuV4\nyXH+u+s/fLU9jhXpP1BmlGHxsHBDq7/wdI9Y2ts6uLpEEZEqp3AWl7OX2Vm5bwVfbY/ju53fOq+8\nviqkO7e1vZ2/tL6VRvUaubhKEZHqo3AWlzlecpzPtnzM2xvfcI5iDGvQgtvajud/2t6uyU8iUmcp\nnKXa5Rbm8GHyfN777S2yC7PxsdTn7o738z/tRtCjcU9dvCUidZ7CWapNRkEG7256k4+S3ye/5BgB\nXgFM7D6ZByIfwuZ9YVddi4jUBQpnqXLpx/by1sa5LNjyvxTaCwn2CeHJ7pO4J+I+zUcWETkHhbNU\nmYyCDF5bN5NPt3xMaVkpYX5XML7rY9zRfiTeFm9XlyciUmMpnKXS5Rcf482Nc51rXrfyD+dv3Z/m\nlta34Wn2dHV5IiI1nsJZKk2xvZhPt3zMa+tmkXUik6B6wUzr8xJ3dbhboSwichEUznLZDMNgUdo3\nvLzmBXYf3UV9T18m9XiWhzqPx9fT19XliYjUOgpnuSw/71/J9MTn2ZCxHouHhQeufIgnrnqaIJ8g\nV5cmIlJrKZzlkmzO3MT0NVNZkf4DADe3/ivP9Hyelv6tXFyZiEjtp3CWi7IzL41ZSS/xTerXAPQL\nHcCzvabSJbibiysTEXEfFxTOM2bMYNOmTZhMJmJjY4mMjHRuW7BgAYsWLcLDw4NOnTrx7LPPsnDh\nQl5//XXCwsIA6NOnDw8//HDVdCDV4nDBYV77ZSafbf2E0rJSugR15bneL9A3tL+rSxMRcTsVhvPa\ntWvZs2cPcXFxpKWlERsbS1xcHAD5+fl88MEHLFmyBIvFwv3338/GjRsBGDp0KJMmTara6qXK5RXl\n8tbGuby76S0KSgto5R9ObM/nuTH8Zi2zKSJSRSoM58TERKKjowEIDw8nLy+P/Px8fH198fT0xNPT\nk4KCAnx8fDhx4gT+/v5VXrRUjTKjjNScHazPWMe6Q7+wPmMdW4+kYDfshPg05sWoV7ij/UjdFiUi\nUsUqDOesrCwiIiKcj202G5mZmfj6+uLl5cX48eOJjo7Gy8uLYcOG0bJlSzZs2MDatWsZPXo0paWl\nTJo0iY4dO1ZpI3K2E6UnSDywipKyEvyz65F39ASGYZzxmpKyYlKyNvPr4XVsyFjP0eI85zZvszfd\nQrpzXcthjO40Bh9Pn+puQUSkTrroC8JO/+Gen5/Pu+++y+LFi/H19eWee+5h27ZtdO7cGZvNRv/+\n/dmwYQOTJk3i22+/LfdzAwN9sFjMF99BJQoKcp91nlMyUhj+zXC2ZG654Pe0sbXhL6E30bNZT3qG\n9iQyJBKr2VqFVVY+d/oenov6q93cvT9w/x6rq78Kwzk4OJisrCzn44yMDIKCHPewpqWl0bx5c2w2\nGwDdu3cnOTmZ2267jfDwcAC6du1KdnY2drsds/n84ZuTU3BZjVyuoCA/MjOPubSGymAYBgu2/i/P\n/vw0J0pPcGf7UbS1tce3vhf5x4sAMHHqXLHJBG0D29E1+CoCvW1nfFZedhFQVJ3lXxZ3+R6ej/qr\n3dy9P3D/Hiu7v/KCvsJwjoqKYt68eYwYMYKUlBSCg4Px9XWs+tSsWTPS0tIoLCzE29ub5ORk+vXr\nx/z582nSpAk33HAD27dvx2azlRvMUjmOFR9l4orH+Cb1a/y9Ang7+gOGtroBcP+/NCIi7qTCcO7W\nrRsRERGMGDECk8nE1KlTWbhwIX5+fsTExDB69GjuvvtuzGYzXbt2pXv37oSGhvLUU0/x5ZdfUlpa\nyssvv1wdvdRpmzI28OCSe9l9dBfdQ3rw7uAPae4X5uqyRETkEpiMP18h5CKu3qurrXuWhmHw/uZ3\nmLb6OUrKSni069+Y1OPZs66orq39XQx371H91W7u3h+4f4816rC21FyZBZk8+eOjLN71HY3qNeKN\nQe8xMCza1WWJiMhlUjjXIgfy97Pm4GqSDiay5kAi27K3YGBwbbN+vBU9n5D6jV1dooiIVAKFcw1V\nWFrIzrw01h1ay5qDq1l7cA17j+1xbq9nqUdUs2sZ2vIG7uv0IGYPXXAnIuIuFM4uZBgGGQWH2ZG7\nndScHaTl7nD8PjeV9KN7MDh1OUCgVyDXtRhKzyZ96NW0N1c26lzr7kEWEZELo3B2gQP5+3ln05t8\nue0zcotyz9oeVC+YXk370DqgDZFBXejVpA9tAtviYfJwQbUiIlLdFM7VaHv277y58XW+2h5HSVkJ\nwT4hDGt1E20C2hIe0JrWgW1oHdAGf68AV5cqIiIupHCuBusOrWXuhn+weNd3ALQOaMOEro9za9vh\neJm9XFydiIjUNArnKmIYBsv2LmHehn+SeGAVAN2Cr+KRbn/j+pbDdIhaRETOS+FcBQ7k7+eRZWP5\naf+PAAwMi+aRrk/Qp+k1moEsIiIVUjhXsv+kLeJvKyaQW5RLdNhgnun1PFc2inR1WSIiUosonCvJ\n8ZLjTPl5Mp9t/QRvszez+s7h3ojR2lMWEZGLpnCuBJsyNjA2YTRpualENLySd2M+pK2tnavLEhGR\nWkpXJV2GMqOMeRv+ydCF0aTlpjK28wQW3/aDgllERC6L9pwvUpG9iGPFx8goOMxzP0/i5/0rCfYJ\nYd7AdxgQNsjV5YmIiBtQOJ/DtuytvLHhnxzI38/R4qMcc/46RpG96IzXXtdiKP8Y8CYN6zV0UbUi\nIuJuFM6nyS48wuy1M/gk5UPshh0AH0t9/Kx+BHgFEuZ3Bb7WBjSwNsDP6kefptcwvN0duuhLREQq\nlcIZKLGXMC9pHs8vf57colxa+YfzYtQMBobFYPHQH5GIiFSvOp88y/cu4/lVz/B7zjb8rA14oc8M\nRl85RhOfRETEZepsOKfl7mDqqmdZsmcxJkyM6TaGxyInEeQT5OrSRESkjqtT4WwYBokHVvHplo9Z\nlPYNJWUl9Gl6DdOvmcnADlFkZh5zdYkiIiJ1I5wzCjKI+/1zFmz5hJ15aQCEB7QmtudUbmh1ky7o\nEhGRGsVtw9leZufHfT/w2Zb/ZfHu7ygtK8Xb7M1tbW9nVMd76dWkj0JZRERqJLcM5+93/ofnfp7E\nvvx0ADo27MSojvdwa5vhBHgHurg6ERGR8rllOP+wN4HswmxGdriHkR3voWvwVdpLFhGRWsMtw/nv\n/f7BrL6vYfYwu7oUERGRi+aW4WwymTCbFMwiIlI7aSqViIhIDaNwFhERqWEUziIiIjWMwllERKSG\nUTiLiIjUMApnERGRGuaCbqWaMWMGmzZtwmQyERsbS2RkpHPbggULWLRoER4eHnTq1Ilnn32WkpIS\nJk+ezIEDBzCbzbzyyis0b968ypoQERFxJxXuOa9du5Y9e/YQFxfHyy+/zMsvv+zclp+fzwcffMCC\nBQv44osvSEtLY+PGjfznP/+hQYMGfPHFF4wdO5bXXnutSpsQERFxJxWGc2JiItHR0QCEh4eTl5dH\nfn4+AJ6ennh6elJQUEBpaSknTpzA39+fxMREYmJiAOjTpw/r16+vwhZERETcS4XhnJWVRWDgqWER\nNpuNzMxMALy8vBg/fjzR0dEMGDCAzp0707JlS7KysrDZbI4v4OGByWSiuLi4iloQERFxLxe9fKdh\nGM7f5+fn8+6777J48WJ8fX2555572LZtW7nvOZ/AQB8sFtcuuRkU5OfSr1/V3L0/cP8e1V/t5u79\ngfv3WF39VbjnHBwcTFZWlvNxRkYGQUFBAKSlpdG8eXNsNhtWq5Xu3buTnJxMcHCwc++6pKQEwzCw\nWq3lfh1XB7OIiEhNUWE4R0VFER8fD0BKSgrBwcH4+voC0KxZM9LS0igsLAQgOTmZFi1aEBUVxeLF\niwFYvnw5PXv2rKr6RURE3E6Fh7W7detGREQEI0aMwGQyMXXqVBYuXIifnx8xMTGMHj2au+++G7PZ\nTNeuXenevTt2u53Vq1dzxx13YLVamTlzZnX0IiIi4hZMxoWcEBYREZFqoxXCREREahiFs4iISA2j\ncBYREalhLvo+59rkYtcELy0t5dlnn2Xv3r3Y7XaefvppunfvzqhRoygoKMDHxweASZMm0alTJ1e1\n5XSx/S1cuJDXX3+dsLAwwLF628MPP8y2bduYNm0aAO3ateOFF15wRTtnudj+3n77bVavXg1AWVkZ\nWVlZxMfHM3DgQBo3bozZ7Lhd79VXXyUkJMQlPf1ZeT0mJCTw9ttvY7VaGTZsGCNHjjzvew4ePMjT\nTz+N3W4nKCiIv//97xXevlgdLqW/2bNn8+uvv1JaWspDDz3E4MGDmTx5MikpKQQEBAAwevRo+vfv\n74qWznCx/SUlJfHYY/aNF9kAAAdaSURBVI/Rpk0bANq2bcuUKVPc5vv3//7f/2PRokXO1yQnJ7Nh\nw4Ya+zMUYPv27YwbN457773X+f/gH1avXs2cOXMwm8307duX8ePHA9X0d9BwU0lJScaYMWMMwzCM\n1NRUY/jw4c5tx44dMwYMGGCUlJQYhmEY9913n7Fhwwbjq6++MqZOnWoYhmFs377duPXWWw3DMIyR\nI0cav//+e/U2UIFL6e/rr782Zs6cedZnjRw50ti0aZNhGIbxt7/9zVixYkU1dFC+S+nvdAsXLjTm\nz59vGIZhDBgwwMjPz6+myi9ceT3a7Xajb9++xpEjRwy73W7cf//9xsGDB8/7nsmTJxvff/+9YRiG\n8dprrxkLFiyo5m7Odin9JSYmGg888IBhGIaRnZ1t9OvXzzAMw5g0aZLxww8/VHsP5bmU/tasWWM8\n8sgjZ32Wu3z//vz+adOmGYZRM3+GGoZhHD9+3Bg5cqTx3HPPGZ9++ulZ26+//nrjwIEDht1uN+64\n4w5jx44d1fZ30G0Pa1/KmuA33XQTzzzzDOBYpjQ3N9dl9VfkUvo7l+LiYvbv3+/8F/GAAQNITEys\nnibKcTn9lZaW8sUXX5z1r+Caprwec3JyaNCgATabDQ8PD3r16sXq1avP+56kpCQGDRoE1I7v4fn6\nu/rqq3n99dcBaNCgASdOnMBut7ush/JcSn/n4y7fv9O9+eabjBs3rtrrvhhWq5X58+cTHBx81rb0\n9HT8/f1p0qQJHh4e9OvXj8TExGr7O+i24Xwpa4J7enri5eXF/2/v/kKa/OI4jr9Hk9xiVE4Y2ZCw\ni9Qb8SYw00QwNCLtUoQVrYsgDYRMCJxXYcsRYRqaGggVE1dEZOCQvIiCUAjCRMQLaQlaugv/Ekr7\nXQzPr/Vz6ga/7dn4vu72wHnww9dzjjvP8TwAfX19nD9/XrVva2ujpqYGh8OhDl2Jp2jyQfAtY3a7\nnUuXLjExMaE62Raz2azuE0/R5gPwer2cPn2a1NRUda25uZnq6mpcLteejpONhZ0ypqWlsbq6yszM\nDBsbG3z69ImFhYWwbdbX19USWiLUMFy+ffv2qaVPj8dDcXGxehzx9OlTbDYb9fX1+P3+2Af6SzT5\nAKanp7l27RrV1dV8+PABIGnqt+XLly8cOXJEnSYJ2htDAfR6fcg48aefP3+qd0TAv/lj1QeT+pnz\nnwJ7OBM8OzsbCD7P/Pr1K52dnQDYbDZOnDhBZmYmzc3NPHv2DLvdHpcc4ewlX15eHmlpaZSUlPD5\n82caGxvp6ekJex8tiaR+L168CHlufuPGDYqKijh48CDXr19naGiI8vLymGfYzZ8ZdTodd+/e5fbt\n25hMJqxW665tdrqmBZHkGx4exuPx8OTJEwAqKys5dOgQOTk5PH78mPb2dhwOR0x//t3sJd+xY8eo\nra2loqICn8+HzWbD6/WGvY+WRFI/j8fDxYsX1edEGEOj9X/1waT95hzNmeAAAwMDvHv3jkePHpGS\nkgJAWVmZ2kRVWlrK1NRUjNP8VzT5jh8/rjbR5Ofn4/f7OXz4cMjy/fz8/LZLPLEWbf3W1taYm5sL\nGSyqqqowm83o9XqKi4s1UT/YOSPAyZMnef78OV1dXZhMJo4ePRq2jdFoVN9GEqGGsH0+gPfv39PZ\n2Ul3dzcmU/AlAwUFBeTk5ACJ0Qdh+3wWi4Vz586h0+nIzMwkPT2d+fn5pKofBJfp8/Pz1WctjqG7\n+Tv/Vl1i1QeTdnKO5kxwn8+H2+2mvb1dLW8HAgEuX77M0tISEPyl29ppGU/R5Ovu7ubNmzdAcIfi\n1uSWlZXF2NgYEFwSLioqikOiUNHkA5icnCQrK0vdZ3l5Gbvdrl5ZOjo6qon6wc4ZAa5evcri4iJr\na2uMjIxQUFAQts2pU6fU9USoIWyfb3l5mXv37tHV1aV2ZgPU1dXh8/mAxOiDsH2+169f09vbCwSX\nTRcXF7FYLElTPwhOTAcOHFBLvFodQ3djtVpZWVnh+/fvbG5uMjIyQmFhYcz6YFIf3+lyuRgbG1Nn\ngk9MTKgzwd1uNy9fvlRngt+6dYv79+8zODhIRkaGukdvby/Dw8P09PRgMBiwWCzcuXMHg8EQx2RB\nkeabm5ujoaGBQCDA5uam+heA6elpHA4Hv3//Ji8vT22Ki7dI8wEMDQ3x8ePHkGXtvr4+Xr16xf79\n+8nNzaWpqQmdThevWCF2yuj1euno6ECn03HlyhUuXLiwbZvs7Gx+/PhBY2Mjv379IiMjg5aWFrXy\nE0+R5uvv7+fhw4chewicTiffvn2jtbUVg8GA0WikpaUFs9kcx2RBkeZbWVnh5s2bLC0tsbGxQW1t\nLWfOnEma+kHwj+UHDx6EPDJ7+/atJsfQ8fFxnE4ns7Oz6PV6LBYLpaWlWK1WysrKGB0dxeVyAXD2\n7Fm1FB+LPpjUk7MQQgiRiJJ2WVsIIYRIVDI5CyGEEBojk7MQQgihMTI5CyGEEBojk7MQQgihMTI5\nCyGEEBojk7MQQgihMTI5CyGEEBrzD0A0T+oVHBw1AAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 806
+ },
+ "outputId": "7bc4b0e7-e55a-47b5-8d2a-7ad23d5b1d73"
+ },
+ "cell_type": "code",
+ "source": [
+ "# YOUR CODE HERE\n",
+ "linear_regression(learning_rate=0.000004, n_epochs=100000,interval=4000)"
+ ],
+ "execution_count": 32,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.066218026\n",
+ "Loss after epoch 4000 is 0.065922044\n",
+ "Loss after epoch 8000 is 0.06562787\n",
+ "Loss after epoch 12000 is 0.065336615\n",
+ "Loss after epoch 16000 is 0.06505493\n",
+ "Loss after epoch 20000 is 0.06477268\n",
+ "Loss after epoch 24000 is 0.06449185\n",
+ "Loss after epoch 28000 is 0.06421243\n",
+ "Loss after epoch 32000 is 0.063934416\n",
+ "Loss after epoch 36000 is 0.06366609\n",
+ "Loss after epoch 40000 is 0.06339979\n",
+ "Loss after epoch 44000 is 0.06313459\n",
+ "Loss after epoch 48000 is 0.06286868\n",
+ "Loss after epoch 52000 is 0.06260253\n",
+ "Loss after epoch 56000 is 0.062337458\n",
+ "Loss after epoch 60000 is 0.062078353\n",
+ "Loss after epoch 64000 is 0.06182364\n",
+ "Loss after epoch 68000 is 0.061569765\n",
+ "Loss after epoch 72000 is 0.06131672\n",
+ "Loss after epoch 76000 is 0.061064526\n",
+ "Loss after epoch 80000 is 0.060813166\n",
+ "Loss after epoch 84000 is 0.060562644\n",
+ "Loss after epoch 88000 is 0.060312964\n",
+ "Loss after epoch 92000 is 0.06006835\n",
+ "Loss after epoch 96000 is 0.059827697\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.22594003\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xl8FPX9x/HXZndz32GTkIRwn0EQ\nBBGQ03Aoaqm1ihXRgtVW1Gr1hxoP7AFqi/5atQelaP0pVariTUFR8CJyiwUEJJIDEnIn5M5uMr8/\nAktCAoGQZJLl/Xw8eCSzM/Pd72eX5J3vd2ZnLIZhGIiIiEi78zK7AyIiIucrhbCIiIhJFMIiIiIm\nUQiLiIiYRCEsIiJiEoWwiIiISWzt/YS5uSXt/ZQNhIX5U1hYbmof2pqn16j6OjdPrw88v0bVd/Yc\njqAmHz/vRsI2m9XsLrQ5T69R9XVunl4feH6Nqq/1nHchLCIi0lEohEVEREyiEBYRETGJQlhERMQk\nCmERERGTKIRFRERMohAWERExSbtfrKMjeu65/2Xfvm8pKMinsrKSmJhYgoNDWLz4D63S/rXXXkVk\nZBReXif+5nn++b+fc7tffPEpo0aN4ejRYpYvX8qCBQ+fc5siItJ+ziiE9+/fzx133MEtt9zC7Nmz\nG6zbuHEjzzzzDFarlfHjxzN//vw26WhbuuuuewFYvfo9vv8+hTvvvKfVn2PJkmfx9/dv1TZfe20F\nw4ePJCKiiwJYRKQTajaEy8vL+e1vf8vo0aObXP+73/2O5cuXExUVxezZs5k2bRp9+vRp9Y6aYfv2\nrbz22iuUl5dz5533ct99d/LBBx8D8MgjC7jmmusYMGAgixf/mpKSEmpqarjnnv+hT5++Z9T+jBmX\nNWpvx45tlJWVkp6exuHDh7j77vsYPXosa9Z8wBtvrMRisTBr1o04nU727NnF/fffzYMPPsqvf/0I\ny5e/zPbtW3nxxaUYhgWHI5KHHnqMdevW8s03X1NUVEh6eho/+clNXHnlzDZ73URE5Mw0G8Le3t4s\nW7aMZcuWNVqXkZFBSEgIXbt2BWDChAkkJyefUwg/vvER3kt5u8X7N+Wq3jN5fMzvWrRvSsoBXn11\nFd7e3k2u//e/X2XUqDFcddVMDh78nj/9aQl//ONfzqW75ORks2TJs3z11UbeeedNhg69kH/+8x+8\n9NKrVFc7WbRoIU8++Qz/+MffWLLkWYqLi9z7LlnyBP/3fy9hswXyzDNP8dFHa7BYLKSkHOBvf3uB\nQ4cyWLgwSSEsInKS6ppqkjO/xJVdzuTIK7BYLG3+nM2GsM1mw2ZrerPc3FzCw8Pdy+Hh4WRkZJy2\nvbAw/9Nel9Pfzxsvr9Yt3N/Pu8HFs091Ie2gIF/8/U9sGxrqz6BBA4mNjQDAYrG41/n42AkN9Wff\nvt0UFBSwfv2HAFRVVTRq32r14qGH7sVqras7LCyMZ599tsn2AgJ8GD16FA5HEP3796SqqoLi4hz6\n9u1DXJwDgOXLl7nb7dIlEKvVic3mhd1eg81mdf9RNHHiOLZs2cKgQYMYOfIioqNDCQqyU1FRdsrX\noLPo7P1vjurr/Dy9Rk+pL7s0m/8c+A/v73+fD1M+pKS67iZDWfdlER0Y3ebP3+4nZjV3Z4oFwx5j\nwbDHWv15j9+9yeEIOuWdnEpKKikvr3avLyoqxzAs7mXDMNzfl5VVuNffddd9DB48pNFzHVdTU8sT\nT/xvg2PCubklTbZXVlaF3e5Hbm4JhYVlVFe7KC6upLKyusl28/JKKS4uw+WqJT+/DJerxt1+fv5R\nKitdlJRUUl1dS25uCeXl5dTU1Jp+N6tzcbr30BOovs7P02vsqPUZhkHq0YNUuCrw9vLG5mXD2+qN\nzcuOt5cdm9WO3cvO/sJ9fJS6ho/S1rA9exsGBgA9gntyw4DZ3DxiNtaKAHIrWq/GU/3Rck4hHBkZ\nSV5enns5OzubyMjIc2myQ7NYLFRWVgKwf/8+AAYNGsxnn21g8OAhHDz4PZs2bWTWrNmna+a07TWl\ne/cepKenUV5ejtVq5YEH7uV///fPWCxe1NTUuLcLDg7GYrGQmZmJ3R7E119vZ8iQCxtsIyLiKQzD\n4GBxCl8c/pwvD3/Gl5lfkFOefcb7Wy1WxsRcypQe05nafTq9Q/u4Zyjb64+McwrhuLg4SktLOXTo\nENHR0axfv54lS5a0Vt86nJkzr+W2226mR49e9O8/EIBrr72eRYse5447bqW2tpZ77rn/nNprip+f\nH/Pm/Zx77rkDgOuv/wkWi4Vhw4Zzxx3zePjhx93bLljwCPfddx+1tRAbG8dll03lww//07KCRUQ6\nEMMwSDuaypeHP+eLw5+xMfMLssoy3esdfpHM7HMN4b4ROGudOGudVNdU46p1UV1bjavGSXWtkyj/\nKKZ0n8ak+MsI8Qk1sSKwGIZhnG6DXbt28dRTT3H48GFsNhtRUVFMnjyZuLg4pkyZwpYtW9zBO3Xq\nVObNm3faJzR7CqOjTqO0Jk+vUfV1bp5eH3h+je1ZX3Z5Nl8c+pTPD33K54c/JaMk3b2ui18XxsSM\nY2zsOC6NHU+f0L6tcjJVW9TX4unowYMH8/LLL59y/ciRI1m5cmXLeyYiInJMSfVRNmZ+yeeHNvDZ\noQ3sLfjWvS7UJ5QZva7m0thxjI0dT/+wAe1yBnNb0hWzRETEVNnl2byf8g7vp7zDV1kbqTHqzmPx\ns/kxsdtkxsVNZHzsBAZ3GYLV69SfrumMFMIiItLujpRl8X7KO7z3/Tt8lbnRfYbyRVEjmBA3iXFx\nExkRfTE+Vh+Te9q2FMIiItLmSqtLyCzN5NNDn/BuyttszvoKAwMLFi7ueglX957Jlb1+QNfAGLO7\n2q4UwiIick4Mw+BQaQbbs7dyuPQwR8qyyC7LIrs8u+778mzKnKXu7S1YuCRmDFf3nsmMXlcTHdDV\nxN6bSyEsIiJnpaa2hv/mfcPmrGQ2ZSWzOWsTmWWHm9y2i18XegT3JCogiij/aIY4LuTKXlcTFdD2\nV6PqDBTCQFZWJnPmzKJ//wEAVFdXc+ONNzNhwqSzbuvNN1dSVFTE+PET+eyzDcybd3uT2x2/DaHd\nbm+2ze+/P8Azz/y+0e0PJ0wYxQUXDHUvR0RE8OtfP3HWfT7Z+vXrmDQpke++23faGkTk/FBSfZTt\n2dvYmr2ZTVnJbMve4r68I0AXPwdX9LyKkdGj6BnSi+iAaKL8o3H4R+Jtbfq6+1JHIXxMfHx3d8gd\nPVrMT396I5dcMhofH98Wtde3b3/69u1/yvXHb0N4JiF8KoGBga1yX+KTvfLKS0yalNhsDSLieWpq\na9hfuI9t2Vvc//YV7HWfOAXQP6I/IyJHcXH0JYzqegk9Q3p3+o8KmUUh3ITg4BAiIrqQn5/Piy8u\nw2azc/RoEb/5zZP8/veLyMw8jMvl4tZbf85FF41k69bNPPvs04SHRxAR0YWYmFi2b9/KqlX/5ne/\n+/1pb0P4pz/9lXfffYt169ZgsXgxbtxEbrhhNjk52Tz66IPY7Xb69Ol3xn3Pysrk9tsfYunSlwCY\nN+8mfve7p3jhhb/TpYuDffu+JTv7CI899jv69x/AihUvsWHDx1gsXvz853eyd+8eDhzYT1LS/3Dt\ntde7a/j4449YuXIFVquV/v0Hcs8997N8+dImb7soIp1HrVHL1znb+SR9HclZG9mRvY1S54lRrr8t\ngDExl3JR1Eguih7JyOhRDIzv6dEXI2lPHS6EAx5/BJ/3WvdWhlVXzaTs8TO/lWFWViZHjxYTGRkF\n1F2T+YEHHmbNmg+IiOjCQw89RlFREb/85c956aXXWLr0eR599Lf07duP+++/m5iYWHdb5eVlp70N\nYW5uDhs2fMxf/rIcgF/8Yh6TJiWyatVKLrtsKtdddwOvvPJPDhzYf86vQ3V1Nc888zxvv/0Ga9Z8\ngL+/Pxs2fMzSpf8kM/Mwr7zyTx588FFWrHiJxYv/wPbtW4/VUM7f//5nXnzxX/j7+7Ngwb3udSff\ndlEhLNLx5VXksT59HR+nf8SnGZ+QX5nvXtc3tB8XRV9dF7pRIxkQPhCbV4eLCo+hV/aY9PQ07rzz\nNqDuHsqPPPJr9y0cBw1KAGDXrm/YuXMH33zzNQBVVVU4nU6ysrLo27dutHrhhcOpqqpyt5uaepD4\n+B74+Pji4+PLk08+0+B5v/12N4cOZXDXXXXHXcvLyzhyJJPU1INMmpQIwLBhI/jqq42N+lxaWuru\nM0Dv3n1Oe/OIoUOHAeBwRLFnz27279/HoEGD8fLyIi6uGw8++GiT+2VkpBMXF+++C9SwYRexf/9e\nAIYMuRCou5lHaWlpk/uLiLlqjVq2Z29lXfqHfJL2ETtzv3ZPL0cHdOUnA27isu5TuDR2PGG+4c20\nJq2pw4Vw2eO/O6tRa2upf0z4ZDab3f11zpy5TJkyvcF6Ly8v9/cnX4rby8uKYdSe8nltNjujR49l\nwYKHGzy+YsVLWCxex9psev+mjgkfOZLVYNnlcrm/P34/4+P9tFq9qK097aXDAbBYGtblcjnx8fFp\nsk0R6RhctS6+ytrI+ynvsPrg+xwpq/vdYPOyMSbmUibFJ3JZ/BQGRSToeK6JvJrfRI4bNGgwX3zx\nKQCFhQUsXfpnALp0cZCenophGOzYsa3BPvVvQ1hVVcU999yBYRju2xD27z+Q7du3UVlZiWEY/PGP\nS6iqqiQ+vjt79+4BcE/9ngl//wDy8/MxDIP8/DwyMw+dctv+/Qfy3//uxOVyUVCQz0MP1d0B6uRg\n7tatO4cOpVNeXgbAjh3b6d9/0Bn3SUTah7PGySfp67hvw90Meakf17xzJS/sWkalq4JZA27kxekr\n2Dc3lbdmfsDdw+8loctgBbDJOtxIuCObPDmR7du38POfz6Wmpoa5c+umgm+77Q4eeeQBoqO7uo8j\nH9fcbQife+7vXHfdDcyf/zO8vLwYP34iPj6+/PjHN/Doow/y2Wfr6d277xn3MTg4mDFjxnDrrXPo\n06fvac9u7to1hmnTruDOO2/DMAxuv30+AP369ednP5vDL35xt7uG+fN/yX333YXF4sWQIRcydOiF\nbN266axePxE5d4ZhUFhVwJGyI8cuilH39bui/XyUtpbiqiKg7rZ+NyfM48peVzMm5lLs1pZ/EkPa\nTrO3MmxtZp9R5+m3GAPPr1H1dW6eXh+cfY3FVUWkH02jsKqQospCCioLKKoqpLCysO5rVSH5FXnu\nwK2urW6yndjAOGb0uoore/2AkdGj2uxmB57+HnaoWxmKiEjrMwyD5Mwv+b89L/B+yrunDNbjrBYr\nUf7RDO5yAVEBXYkOiCbavyvRAV2JCogmNjCOfmH9Nb3cySiERUTaUWFlASv3/YuXd/+T74rqPnrY\nN7QfE7tNJsw3/Ni/MEJ9wgjzCSPUt+5rsE8IXhadxuNpFMIiIm3MMAw2H9nE/+1+gXdT3qKqpgpv\nL2+u6ftjbk6YyyVdx2gEe55SCIuItLIKZwXbsrfwTe5Ovsn9ms1ZX7lHvb1D+3DToJ9yff+fEOEX\nYXJPxWwKYRGRFqpwVZBfkcfh0sPsytvJztyv2ZnzNfsL91Jj1Li387X6MrPPNcxJmMvYmHEa9Yqb\nQlhEhLop4+KqIvIr88iryCe/Io/8yry6rxV55FfWPVZQWUDBse/LXeWN2vG3+TMqbhSDQi9giONC\nhjgupF9Yf136UZqk/xUicl6qNWpZm/of/r7zLxwo+o6Cynyctc5m9/Oz+RHh24U+Yf0I9w0nwrcL\nDv9IBne5gKGOYfQJ7Ut0VKhHf4RHWo9CWETOK65aF28feJNntz/D3oJvAege3IMhjqF08XMQ4duF\nCL8udd/7RdDFr4v7sXDfCPzt/iZXIJ5EISwi54WqmipW7v0Xz+34X9KOpmK1WPlxv1ncPfxX9A8f\nYHb35DylEBYRj1bmLOPlPS/yl6+f40hZFj5WH25JmMf8Yb+ke3APs7sn5zmFsIh0WtU11XxXuJ/c\nihzyKnLr/pXnNVhOKUrhaHUx/rYA7rjwbn4x9E6iAqLN7roIoBAWkU5oT/5uXt37Cm/se63BDelP\n5mP1ISqgK7cPvYNbL7hd98qVDkchLCKdQlFlIW8deJNXv32Zr3N3ABDhG8GNA+cQGxiHwz+SLn4O\nuvg5cPjVnbEcaA/SZ3KlQ1MIi0i7+65wP28feJOP0z7EbvU+diOC6BM3JgjoSteArkT6R7Eteyuv\n7X2FD75/j6qaKrwsXkztPp1ZA2Yztcd0vK3eZpcj0mIKYRFpF6nFB3nnwCreT32bndk7AbB72akx\naqg1apvdv29oP2YNnM11/WbpmK54DIWwiLSZwyWHeCflLd458CY7crYDdcE7rcfl/KDPNUzvcQV+\nNn/yKnI5UpbFkfIjZJVmcqT8xM3qYwLjmDXgJ4yIulhTy+JxFMIi0mqyy46QnPklyVlfkpz5pfti\nGFaLlYndJvPDPtdy08hZuEob/uqJCogmKiCaoWZ0WsRECmERabGMknQ2Hv6Cr7I2kpz5Jd8Xp7jX\n+dn8GB83iSt7Xc2VvX9AF78uAIT5BZFbqks6ioBCWETOQrmznC8Pf8bH6R/xcfpHpB1Nda8L8g4m\nMX4ql8SMZUzMWIY4LtRJUyLNUAiLyCkZhsH3xQf4OK0udDdmfkFVTRUAgfYgpvecwZiYsYyJuZSE\niAuwellN7rFI56IQFpEGqmuq2Zj5BWtTV7Mu7cMGo92B4Qlc1n0Kl8VPYWT0KI10Rc6RQlhEKKjM\n5+O0j1ib+h8+SV9HqbPumG2gPYgZva7msvgpTI5PJCYw1uSeingWhbDIechV6+L7ohTWpX/I2tTV\nbMpKdn9Wt3twD24ceBNTe1zOqK6jNdoVaUMKYREPVGvUklWaSUZJOuklaaQfTSOjJL1u+Wgah0sP\nUWPUAGDBwkVRI5ne8wqm9biCfmH99XlckXZyRiG8ePFidu7cicViISkpiSFDhrjXrVu3jr/+9a94\ne3szY8YMZs+e3WadFZHGKlwV7M3fw+78XezK+4bd+bvYnbfLPaV8suiArgyPGkH34B6Mi51AYvdp\nOPwd7dxrEYEzCOHNmzeTlpbGypUrSUlJISkpiZUrVwJQW1vLb3/7W9566y1CQ0P52c9+RmJiItHR\nuqScSGurqa0hrSSV/QX72F+4lz3Hwva7ov0NLvvoZfGib2g/BoQPontwD7oFxxMf1J344HhiA7vh\na/M1sQoRqa/ZEE5OTiYxMRGA3r17U1xcTGlpKYGBgRQWFhIcHEx4eN3twS655BI2btzINddc07a9\nFvFghmGQUvQde/L3sL9wL/sL9rKvcB8pRd+5Px50XKA9iJHRoxjc5QISIi5gcJcL6B8+ED+bn0m9\nF5Gz0WwI5+XlkZCQ4F4ODw8nNzeXwMBAwsPDKSsrIzU1ldjYWDZt2sTFF1/cph0W8URlzjK+PPwZ\n69I+ZP2hdaQVpzVY72/zZ2D4IPqG9ad/+AD6hQ2gf/gAugf3wMviZVKvReRcnfWJWYZhuL+3WCw8\n+eSTJCUlERQURFxcXLP7h4X5Y7OZ+4F+hyPI1OdvD55eY0euL704nW9zvyXEN4RQ31BCfUMJ8QnB\n1+bb4ISnAwUHWP3dalZ/t5oNqRvco9wQnxB+POjHjIodxSDHIAY5BtEtpJtHhW1Hfv9ai6fXqPpa\nR7MhHBkZSV5enns5JycHh+PESRwXX3wx//rXvwB4+umniY09/ecICwvLW9rXVuFwBJGb69nXrfX0\nGjtifbVGLZ9mrOfFXcv4MG1Nk7fm8/byJtgnhBCfEJw1TtJLTox2B0UMJjF+Kondp3L5BZdRmF9x\nYkcn5OeVtUcZ7aIjvn+tzdNrVH0ta7MpzYbw2LFjee6555g1axa7d+8mMjKSwMBA9/pbb72Vp556\nCj8/P9avX89Pf/rT1uu1SAd3tKqY1/au4MXd/yCl6AAAwyKHk9h9GhWuCoqrijlaVczR6rp/xVV1\n/1y1Tq7oeRWJ3ac2ugiGzUufHBQ5XzT70z58+HASEhKYNWsWFouFhQsXsmrVKoKCgpgyZQrXXXcd\nc+fOxWKxcNttt7lP0hLxZHvyd/PCf5fxxv6VlLvK8LH6cF3/G5g7+GcMjxphdvdEpJM4oz+577//\n/gbLAwYMcH8/depUpk6d2rq9EulgSp2lbMnaRHLml3x+eAPbsrcCEBfYjV8NXsCNA+cQ4Rdhci9F\npLPRvJdIE0qqj7I56ys2Zn7Jxswv2Jm7A1etC6j7HO6EuEnMu+B2pnSfpjsHiUiLKYTlvGcYBqlH\nD7I9eyvbsrewLXsL3+TudF/W0WqxcmHkMEbHXMrYmEu5uOslBHkHm9xrEfEECmE57xRXFbEjZzvb\nsrewPXsr27O3kl+Z715v87IxPGoEY2IuZXTMWC6OHkWgt2d/HENEzKEQlvNCVmkm76W8zTspb7H1\nyGYMTnzevVtQPJfGTuCi6BEMjxzJBY4huuKUiLQLhbB4rKzSTN7//h3eOfAWm498BdQdzx3VdTSj\nuo5meNQIhkeNIMo/yuSeisj5SiEsnUJNbQ1bjmxifcY6rN5gcdnxtwXgb/fH3+aPvz2AAHsA/jZ/\nduV9wzspb7E56ysMDCxYGBszjqv7/JAZva4m0j/S7HJERACFsHRgpc5SNqR/wtrU1XyUtoaCyoIz\n3teChdExY7mq90yu7P0DjXZFpENSCEuHkl12hLWp/2HNwQ/4/PCn7uspR/lHM2fQXKb2mEafrt05\nnJtLuaucMmcp5c5yyp1llLvKKXeWEx3YlRk9ryIqQLfUFJGOTSEspilzlvHfvG/4OmcbX+dsZ0fO\ndg4Wf+9ePzA8gek9L2d6jxkMjRzmvoGBwxFEro/nXrdWRM4fCmFpF4ZhsL9wH19lbXQH7t6CPQ1u\ndBDiE8rEbpO5LH4K03pcQY+Qnib2WESk7SmEpc3kV+Tz+aENrM/4mA0Zn5BVlule52fzY2T0KC6M\nHM6wyOFcGDmcnsG9GtzqT0TE0ymEpdVU11Sz9chmNmR8woaMj9mZ+7X787gRvhFc0/daLo2dwLDI\ni+gfPkB3CxKR855+C8o5OVpVzMfpH/Gfg++zLu0jSp11x2rtXnbGxFzKxG6TmdhtMhc4hnrUTelF\nRFqDQljOWmbpYdakrmbNwQ/48vDnOGudAMQH9+D6ATcwqdtljIkdR6A9sJmWRETObwphaZZhGOwt\n+JY1Bz9gTeoH7MjZ7l43xHEhl/ecweU9r2Rg+CAd0xUROQsKYWmSq9bFpqxk1hz8gP+krib9aCpQ\nd3OD8XGTuLznFUzrcQVxQd3M7aiISCemEBa30uoSPklfx5rU1axLW0tRVREAgfYgftD7Gqb1vJzE\n+KmE+oaZ3FMREc+gED6PGIZBXkUeGSVpZJSkk1GSUff90XQyStI5WPw91bXVAMQExPLDvtcyvccM\nxsReio/Vx+Tei4h4HoVwJ1dcVcRre1fw6t4VFBy7J66Xl4XaWqPBdoZhcLS6mApXRZPthPiEktBl\nMJfFT2V6zyu4oMtQHd8VEWljCuFOam/Btyz/7995fd9rlLvK8LH6EBMYC4DV6kVNTW2jfSL9o4gP\n7k5cUDfig+LpFtSdbkHxdAvqRrBPSHuXICJy3lMIdyKuWhdrU//D8v8u5YvDnwEQF9iNXw1ewOxB\ncwj3jQCOXVs5V9dWFhHp6BTCHVitUUtm6WHSjqay9chmXtr9AodKMwAYFzuBeRfczrQel2P1sprc\nUxERaQmFsImcNU7yK/PILc8hqyyT1OKDpB496P6afjTNfaIUgL/Nn5sT5jHvgtsYED7QxJ6LiEhr\nUAi3IcMw2Fe4l88PbeBg8ffklueSV5FLbkUOueU5FFYVnnLfUJ9QBkUk0COkJz2Ce9E7tA/Te15B\niE9oO1YgIiJtSSHcyo6UZfFpxno+O7SBzw5tILv8SKNtwn3DcfhHMihiMF38HDj8HUT5Rx8L3J50\nD+6hz+KKiJwHFMLnyFXr4tOMT1if8TGfZqxnX+Fe9zqHXyQ/6nsdE7pNIqHLBUT6RRLuG4Hdajex\nxyIi0lEohFsoqzSTl/f8k1e+fYkjZVlA3T1yJ8cnMiFuMuPjJjIoIkGftRURkVNSCJ+FWqOWzw5t\n4J+7lrM2dTU1Rg2B9iDmDv4ZV/b+ASOjR+nKUiIicsYUwmegoDKf1/b+i//b/QLfF6cAMLjLEG5J\nmMc1/X6sW/aJiEiLnNchvL9gH+99/zbfFe6j0lVFVU0lVTVVVLgqqKqpospVt5xdfoSqmip8rb5c\n3/8n3DJ4HsMjR2iqWUREzsl5FcKGYbArZxcvbVnBeylvNziJqj67lx0fqy++Nh98rL70CxvAtf2u\nZ9aAnxDmG97OvRYREU/l8SFsGAbfFuzh3ZS3eO/A23xXtB8AH6sPl/e8kqt7z2RU19H42/3xsfri\nY/XB5uXxL4uIiHQAHpc2tUYt+wr2suXIJrYc2cSmrGRSjx4E6s5e/tHAHzE1bgZTuk8j0DvI5N6K\niMj5rNOHcEn1UbZlb3WH7vbsbRytLnavD/YO4areM7m690wu6z6VnjFddXMDERHpEDp1CO/I3sbV\nb0+nqqbK/Vjv0D5c0etKRkaPYmT0KPqF9cfL4mViL0VERJrWqUM40j+K6T1m0COkJyOjL+aiqIuJ\n8Iswu1siIiJnpFOHcGxQHMum/dPsboiIiLSI5mlFRERMohAWERExyRlNRy9evJidO3disVhISkpi\nyJAh7nUrVqzg3XffxcvLi8GDB/Pwww+3WWdFREQ8SbMj4c2bN5OWlsbKlStZtGgRixYtcq8rLS1l\n+fLlrFixgldffZWUlBS+/vrrNu2wiIiIp2g2hJOTk0lMTASgd+/eFBcXU1paCoDdbsdut1NeXo7L\n5aKiooKQkJC27bGIiIiHaHY6Oi8vj4SEBPdyeHg4ubm5BAYG4uPjw/z580lMTMTHx4cZM2bQs2fP\n07YXFuaPzWY9956fA4fD86+U5ek1qr7OzdPrA8+vUfW1jrP+iJJhGO7vS0tLWbp0KWvWrCEwMJCb\nb76ZvXv3MmDAgFPuX1hY3rKethKHI8jjr5jl6TWqvs7N0+sDz69R9bWszaY0Ox0dGRlJXl6eezkn\nJweHwwFASkoK3bp1Izw8HG9on0ZnAAAXuklEQVRvb0aMGMGuXbtaqcsiIiKerdkQHjt2LGvXrgVg\n9+7dREZGEhhYdxP72NhYUlJSqKysBGDXrl306NGj7XorIiLiQZqdjh4+fDgJCQnMmjULi8XCwoUL\nWbVqFUFBQUyZMoV58+YxZ84crFYrw4YNY8SIEe3RbxERkU7PYtQ/yNsOzD6O4OnHMsDza1R9nZun\n1weeX6Pqa1mbTdEVs0REREyiEBYRETGJQlhERMQkCmERERGTKIRFRERMohAWERExiUJYRETEJAph\nERERkyiERURETKIQFhERMYlCWERExCQKYREREZMohEVEREyiEBYRETGJQlhERMQkCmERERGTKIRF\nRERMohAWERExiUJYRETEJAphERERkyiERURETKIQFhERMYlCWERExCQKYREREZMohEVEREyiEBYR\nETGJQlhERMQkCmERERGTKIRFRERMohAWERExiUJYRETEJAphERERkyiERURETKIQFhERMYlCWERE\nxCQKYREREZMohEVEREyiEBYRETGJ7Uw2Wrx4MTt37sRisZCUlMSQIUMAyM7O5v7773dvl5GRwX33\n3cdVV13VNr0VERHxIM2G8ObNm0lLS2PlypWkpKSQlJTEypUrAYiKiuLll18GwOVycdNNNzF58uS2\n7bGIiIiHaHY6Ojk5mcTERAB69+5NcXExpaWljbZ76623mDZtGgEBAa3fSxEREQ/UbAjn5eURFhbm\nXg4PDyc3N7fRdq+//jrXXntt6/ZORETEg53RMeH6DMNo9NiOHTvo1asXgYGBze4fFuaPzWY926dt\nVQ5HkKnP3x48vUbV17l5en3g+TWqvtbRbAhHRkaSl5fnXs7JycHhcDTYZsOGDYwePfqMnrCwsPws\nu9i6HI4gcnNLTO1DW/P0GlVf5+bp9YHn16j6WtZmU5qdjh47dixr164FYPfu3URGRjYa8f73v/9l\nwIABrdBNERGR80ezI+Hhw4eTkJDArFmzsFgsLFy4kFWrVhEUFMSUKVMAyM3NJSIios07KyIi4knO\n6Jhw/c8CA41Gve+9917r9UhEROQ8oStmiYiImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwi\nImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiI\niEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIi\nJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiY\nRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhLbmWy0ePFidu7cicViISkpiSFDhrjXZWVl\n8atf/Qqn08mgQYP4zW9+02adFRER8STNjoQ3b95MWloaK1euZNGiRSxatKjB+ieffJK5c+fyxhtv\nYLVayczMbLPOioiIeJJmQzg5OZnExEQAevfuTXFxMaWlpQDU1taybds2Jk+eDMDChQuJiYlpw+6K\niIh4jmZDOC8vj7CwMPdyeHg4ubm5ABQUFBAQEMATTzzBDTfcwNNPP912PRUREfEwZ3RMuD7DMBp8\nn52dzZw5c4iNjeW2225jw4YNTJw48ZT7h4X5Y7NZW9TZ1uJwBJn6/O3B02tUfZ2bp9cHnl+j6msd\nzYZwZGQkeXl57uWcnBwcDgcAYWFhxMTEEB8fD8Do0aP57rvvThvChYXl59jlc+NwBJGbW2JqH9qa\np9eo+jo3T68PPL9G1deyNpvS7HT02LFjWbt2LQC7d+8mMjKSwMBAAGw2G926dSM1NdW9vmfPnq3U\nZREREc/W7Eh4+PDhJCQkMGvWLCwWCwsXLmTVqlUEBQUxZcoUkpKSePDBBzEMg379+rlP0hIREZHT\nO6Njwvfff3+D5QEDBri/7969O6+++mrr9kpEROQ8oCtmiYiImEQhLCIiYhKFsIiIiEkUwiIiIiZR\nCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQh\nLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWw\niIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIi\nIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiElsZ7LR4sWL2blz\nJxaLhaSkJIYMGeJeN3nyZKKjo7FarQAsWbKEqKiotumtiIiIB2k2hDdv3kxaWhorV64kJSWFpKQk\nVq5c2WCbZcuWERAQ0GadFBER8UTNTkcnJyeTmJgIQO/evSkuLqa0tLTNOyYiIuLpmh0J5+XlkZCQ\n4F4ODw8nNzeXwMBA92MLFy7k8OHDXHTRRdx3331YLJZTthcW5o/NZj3Hbp8bhyPI1OdvD55eo+rr\n3Dy9PvD8GlVf6zijY8L1GYbRYPnuu+9m3LhxhISEMH/+fNauXcv06dNPuX9hYfnZ97IVORxB5OaW\nmNqHtubpNaq+zs3T6wPPr1H1tazNpjQ7HR0ZGUleXp57OScnB4fD4V6eOXMmERER2Gw2xo8fz/79\n+1uhuyIiIp6v2RAeO3Ysa9euBWD37t1ERka6p6JLSkqYN28e1dXVAGzZsoW+ffu2YXdFREQ8R7PT\n0cOHDychIYFZs2ZhsVhYuHAhq1atIigoiClTpjB+/Hiuv/56fHx8GDRo0GmnokVEROQEi3HyQd42\nZvZxBE8/lgGeX6Pq69w8vT7w/BpVX8vabIqumCUiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJi\nEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJ\nFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJrGZ3QEREREAamvB6QSnE4uzGqqPf63G4nLV\nfT3+uMt5YtnpOuV2uJxYqqvr2qyuBmc1luPPUV19bL2z7vHqanC5ILYrPP1n8PZu85IVwiIinsgw\n6gKluvpYYJ0i0JzOulCqt139QHIH1/HHnU6wWwgoKj0RlvXbcNZtVxdyx/c5OTidjfvldNb1qyOI\ni8NSUY6hEBYR6SBqapoOjuMjrvrfB9iw5xbXC6amwq/x6M0ddmczeqv/eL12LdXVbfpy+J/Ftoa3\nN4bdG+w2DG8fsNvB15da72Cw2TG87WD3xrDb65Z9vOuWvY8tezdcxvvYtvXbtXvXLdts4OODYbOD\nt/3Y+mNfve11j9uPtel9fF39tuw4okIwckva7LWrTyEsIu3PMOqmHZsKpKZGSU2GX912jacTT1o+\nvm1TAXd81NZEu41Gb7W1Z1ViaFu9dDZb4/Cxe1Mb7NsgSAxv7wYB1zhs6gWX3XYiBI8HnN37WPid\naOt4iIZGhlJYWt3w+ez2hmF3rG2sVrBY2ujV6PwUwiKdnWGcGKU1Ne3ndDYMuPojtkYjrpOOxTmr\nsTibHr01mqp0ndzGsX2djfd1dJBpR8NiOREk9YLDCAjAsIe6Hz8xGmscbo1Gb3Y7AaGBlDqNpkdv\nJ4/KvL3rvvp4n1huKiyPPdYhAs0RhKudRoqeTiEscrJjJ4ecHFynPZZ1qtHUyaO5423VP8Z20ugN\nagkpqzjl6K3J5zMMs181oOG0ozugfHyoDQx0B5Ldz5dqi7Xe6KneiMu9fAajN/eI0A7ePvVGc94N\npiHrT4E2Wme1tsnrEOAIokIhJWdAISxtq/7JIc2N0s7orEYXeFvwLyw5sdzUSST1H693HO3UJ6fU\nmw6tqTH7VcObY9OOTY2afH0xGgXK8eCqNzqz1xu9uacoTz16O7H9Sc/XYPTm3fR0qLc32GxnNEpz\nOIIoVkCJAArhzqf+tGODEzvqBUyAHXtOUeMRl7Op8Gt8xmKzx9SaPEnkNNu1gYCz3L7BtGP90ZSf\nH0ZISOPRW4PjYidNR540emvqONipgsp9sojNfuzkkXrbHdvfERNOblEleOlj/CKe7vwO4VN9Ju10\nJ2e05DNpDR4/9ejtjE5OOcNpx7Y6KeS4BqOjeidl1Pr7Nzmych8XO/aYe8TV4OSQJgKtwXRkXRsh\nkaEUlbsaT1U2OPPRp+EorY2mHduEjw94te2ZrSLSMXTqELZkZxO46HEsRYVn/pk0p5Mux0Oyo5wc\n4uV1Ijjqh09gYONjbKc7OeTY4/4hgZQ5a+ttf+zsR5sdw8enbtrwdKO0U4XiselJ7HZzTw5xBOHU\ndKaIeIBOHcLWg9/j8/prjY7hGfVGRu5pxGOfSfPy9cHlZW0YXO4TO04/emsUVI1Oy683lXnSdqcM\ntzY4OcTfEUS5QkpEpMPr1CHsumQ0+d+lQ03NGX8mzeEIokgBJSIiHUCnDmEAIzDI7C6IiIi0iE6/\nFBERMYlCWERExCQKYREREZMohEVEREyiEBYRETGJQlhERMQkZxTCixcv5vrrr2fWrFl88803TW7z\n9NNPc9NNN7Vq50RERDxZsyG8efNm0tLSWLlyJYsWLWLRokWNtjlw4ABbtmxpkw6KiIh4qmZDODk5\nmcTERAB69+5NcXExpaWlDbZ58sknuffee9umhyIiIh6q2RDOy8sjLCzMvRweHk5ubq57edWqVVx8\n8cXExsa2TQ9FREQ81FlfttKodyu9oqIiVq1axYsvvkh2dvYZ7R8W5o/NZu5t5RwOz7/UpafXqPo6\nN0+vDzy/RtXXOpodCUdGRpKXl+dezsnJweFwAPDVV19RUFDAjTfeyJ133snu3btZvHjxadszO4BF\nREQ6imZDeOzYsaxduxaA3bt3ExkZSWBgIADTp09n9erV/Pvf/+b5558nISGBpKSktu2xiIiIh2h2\nOnr48OEkJCQwa9YsLBYLCxcuZNWqVQQFBTFlypT26KOIiIhHshj1D/KKiIhIu9EVs0REREyiEBYR\nETGJQlhERMQkZ/054Y5o8eLF7Ny5E4vFQlJSEkOGDHGvW7FiBe+++y5eXl4MHjyYhx9+GJfLxcMP\nP0x6ejo1NTUsWLCAESNGcNNNN1FeXo6/vz8ADzzwAIMHDzarLLezrW/VqlX86U9/Ij4+HoAxY8bw\ni1/8gr179/L4448D0L9/f37961+bUU6TzrbGv/71r2zcuBGA2tpa8vLyWLt2LZMnTyY6Ohqrte6j\ncEuWLCEqKsqUmuo7XX3r1q3jr3/9K97e3syYMYPZs2efcp+srCwWLFhATU0NDoeDP/zhD3h7e5tV\nlltL6vv973/Ptm3bcLlc3H777UydOpUHH3yQ3bt3ExoaCsC8efOYOHGiGSU1cLb1bdq0iV/+8pf0\n7dsXgH79+vHoo4922PcPzr7G119/nXfffde9za5du9ixY0eH/T26f/9+7rjjDm655Rb3/8HjNm7c\nyDPPPIPVamX8+PHMnz8faKefQaOT27Rpk3HbbbcZhmEYBw4cMK677jr3upKSEmPSpEmG0+k0DMMw\nfvrTnxo7duww3njjDWPhwoWGYRjG/v37jR/96EeGYRjG7NmzjX379rVvAc1oSX1vvvmm8eSTTzZq\na/bs2cbOnTsNwzCMX/3qV8aGDRvaoYLmtaTG+latWmUsW7bMMAzDmDRpklFaWtpOPT8zp6uvpqbG\nGD9+vJGfn2/U1NQYc+fONbKysk65z4MPPmisXr3aMAzDePrpp40VK1a0czWNtaS+5ORk49ZbbzUM\nwzAKCgqMCRMmGIZhGA888IDxySeftHsNp9OS+r766ivjrrvuatRWR3z/DKNlNZ68/+OPP24YRsf8\nPVpWVmbMnj3beOSRR4yXX3650frLL7/cyMzMNGpqaowbbrjB+O6779rtZ7DTT0ef7trWdrsdu91O\neXk5LpeLiooKQkJCuPrqq3nooYeAustwFhUVmdb/5rSkvqZUV1dz+PBh91+3kyZNIjk5uX2KaMa5\n1OhyuXj11Vcb/WXbkZyuvsLCQoKDgwkPD8fLy4tLLrmEjRs3nnKfTZs2cdlllwEd5z1sSX0jR47k\nT3/6EwDBwcFUVFRQU1NjWg2n05L6TqUjvn9w7jX++c9/5o477mj3fp8pb29vli1bRmRkZKN1GRkZ\nhISE0LVrV7y8vJgwYQLJycnt9jPY6UP4dNe29vHxYf78+SQmJjJp0iSGDh1Kz549sdvt+Pj4APDS\nSy9x5ZVXuvd/9tlnufHGG3nssceorKxs32Ka0JL6oO7uV/PmzePmm29mz5497h+k4yIiIhpcA9xM\nLa0R4MMPP+TSSy/F19fX/djChQu54YYbWLJkSYPLrJrldPWFh4dTVlZGamoqTqeTTZs2kZeXd8p9\nKioq3FNfHeU9bEl9VqvVPV35xhtvMH78ePchhFdeeYU5c+Zw7733UlBQ0P4FnaQl9UHd3eV+/vOf\nc8MNN/Dll18CdMj3D1peI8A333xD165d3VdShI73e9RmszX4HVFfbm4u4eHh7uXjtbfXz6BHHBOu\nr/4v3dLSUpYuXcqaNWsIDAzk5ptvZu/evQwYMACoO9a4e/du/va3vwEwZ84c+vfvT3x8PAsXLmTF\nihXMmzfPlDpO5UzqGzp0KOHh4UycOJEdO3bwwAMP8I9//OOU7XQ0Z/Mevvnmmw2Obd99992MGzeO\nkJAQ5s+fz9q1a5k+fXq713A69euzWCw8+eSTJCUlERQURFxcXLP7nO6xjuBs6lu3bh1vvPEGL7zw\nAgA/+MEPCA0NZeDAgfz973/n+eef57HHHmvX/jfnTOrr0aMHd955J5dffjkZGRnMmTOHDz/88JTt\ndDRn8x6+8cYb/PCHP3Qvd4bfoy3RVj+DnX4kfLprW6ekpNCtWzfCw8Px9vZmxIgR7Nq1C4DXX3+d\nTz75hL/85S/Y7XYApkyZ4j6ZafLkyezfv7+dq2msJfX17t3bfTLLsGHDKCgoICwsrMG0e3Z2dpNT\nM2Zo6XtYXl7OkSNHGvxSmDlzJhEREdhsNsaPH9/h30OAiy++mH/9618sXbqUoKAgYmNjT7mPv7+/\ne2TRUd7DltQH8Pnnn/O3v/2NZcuWERRUd7H80aNHM3DgQKBz/AxC0/VFRUVxxRVXYLFYiI+Pp0uX\nLmRnZ3fI9w9a/h5C3RT7sGHD3Msd8ffo6Zxc+/H3pb1+Bjt9CJ/u2taxsbGkpKS4X7Bdu3bRo0cP\nMjIyeO2113j++efd09KGYXDLLbdw9OhRoO4/1vEzG83UkvqWLVvG+++/D9SdEXg8wHr16sXWrVuB\numnccePGmVBRYy2pEWDv3r306tXL3U5JSQnz5s2juroagC1btnT49xDg1ltvJT8/n/LyctavX8/o\n0aNPuc+YMWPcj3eU97Al9ZWUlPD73/+epUuXus+EBrjrrrvIyMgAOsfPIDRd37vvvsvy5cuBuunO\n/Px8oqKiOuT7By2rEepCKCAgwD0921F/j55OXFwcpaWlHDp0CJfLxfr16xk7dmy7/Qx6xGUrlyxZ\nwtatW93Xtt6zZ4/72tavvfYaq1atwmq1MmzYMBYsWMAzzzzDBx98QExMjLuN5cuXs27dOv7xj3/g\n5+dHVFQUixYtws/Pz8TK6pxtfUeOHOF//ud/MAwDl8vlPrX+wIEDPPbYY9TW1jJ06FD3yWkdwdnW\nCLB27Vo2btzYYDr6pZde4u2338bHx4dBgwbx6KOPYrFYzCrL7XT1ffjhh/z5z3/GYrEwd+5crr76\n6ib3GTBgADk5OTzwwANUVVURExPDE0884Z7JMdPZ1rdy5Uqee+65Bsf3n3rqKdLT0/nDH/6An58f\n/v7+PPHEE0RERJhYWZ2zra+0tJT777+fo0eP4nQ6ufPOO5kwYUKHff+gZf9Hd+3axR//+McGh7tW\nr17d4X6P7tq1i6eeeorDhw9js9mIiopi8uTJxMXFMWXKFLZs2cKSJUsAmDp1qnv6vD1+Bj0ihEVE\nRDqjTj8dLSIi0lkphEVEREyiEBYRETGJQlhERMQkCmERERGTKIRFRERMohAWERExiUJYRETEJP8P\nOCsDxpcSrXYAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ }
+ ]
+}
\ No newline at end of file