diff --git a/Assignment-4.ipynb b/Assignment-4.ipynb
new file mode 100644
index 0000000..3bc43af
--- /dev/null
+++ b/Assignment-4.ipynb
@@ -0,0 +1,955 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "Assignment-4.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "collapsed_sections": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ "[View in Colaboratory](https://colab.research.google.com/github/arghac14/Assignment-4/blob/arghac14/Assignment-4.ipynb)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])\n"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "dabf3a64-06d3-4be4-f74c-b2a56683f1ba"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 109,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const_103:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_104:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_105:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 204
+ },
+ "outputId": "efedfd5d-b8ea-48d4-e99f-c4ecd55f71af"
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 110,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "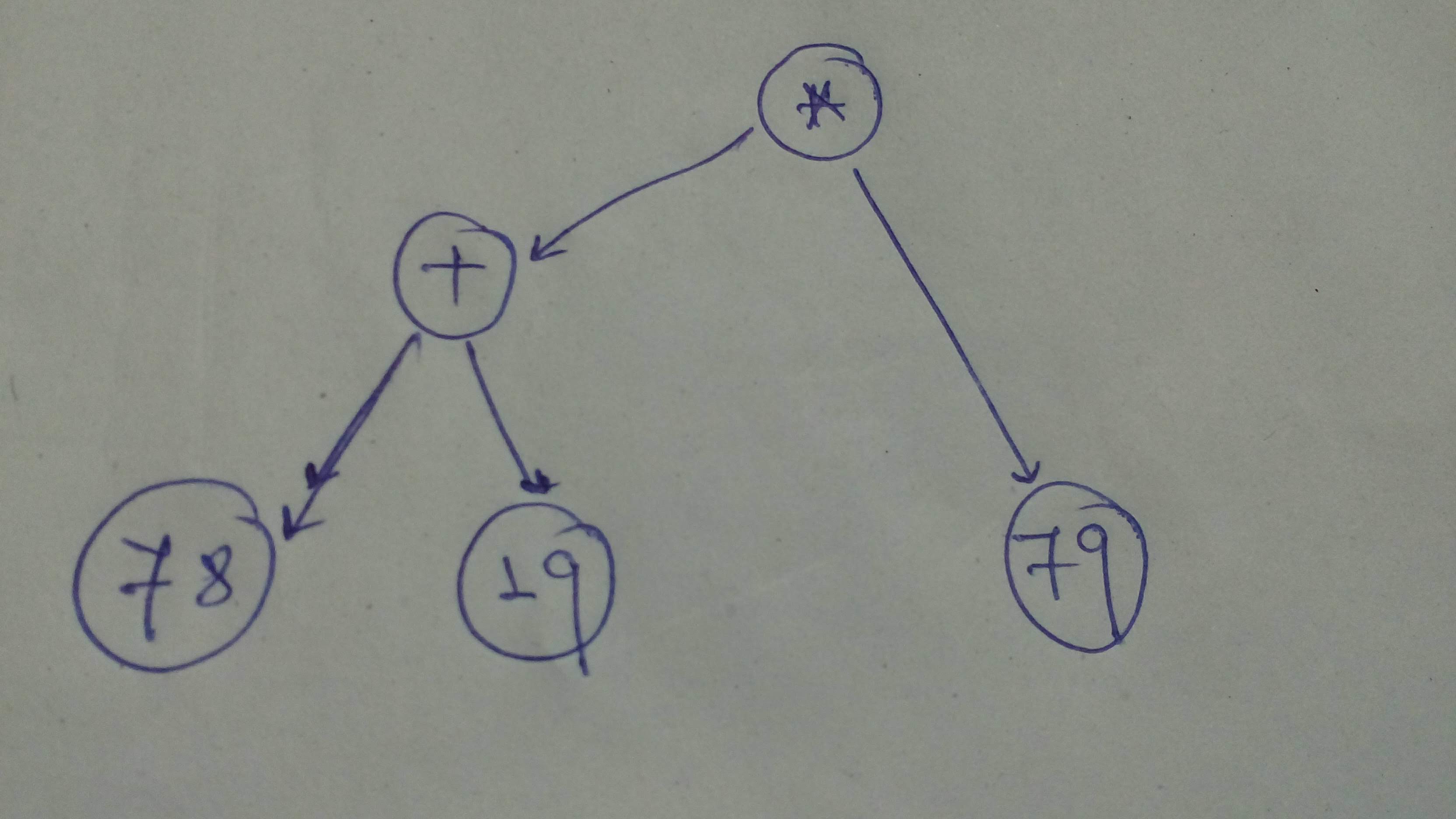"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 51
+ },
+ "outputId": "5fe81bb5-dee9-4b51-a93e-a4a950f6d49b"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 111,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "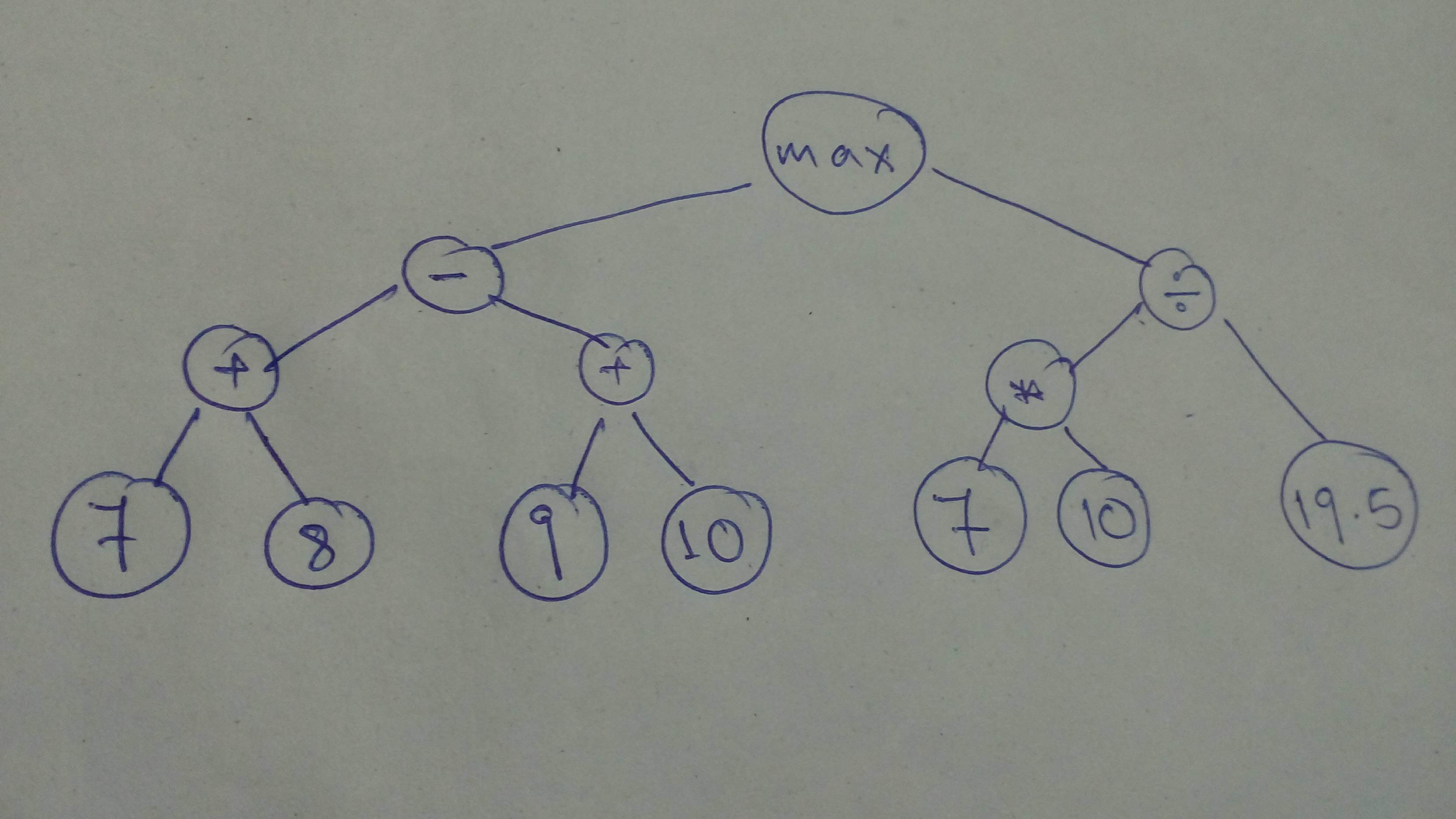"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "35496621-cd71-48bd-ea42-40ff66aa5b77"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 112,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "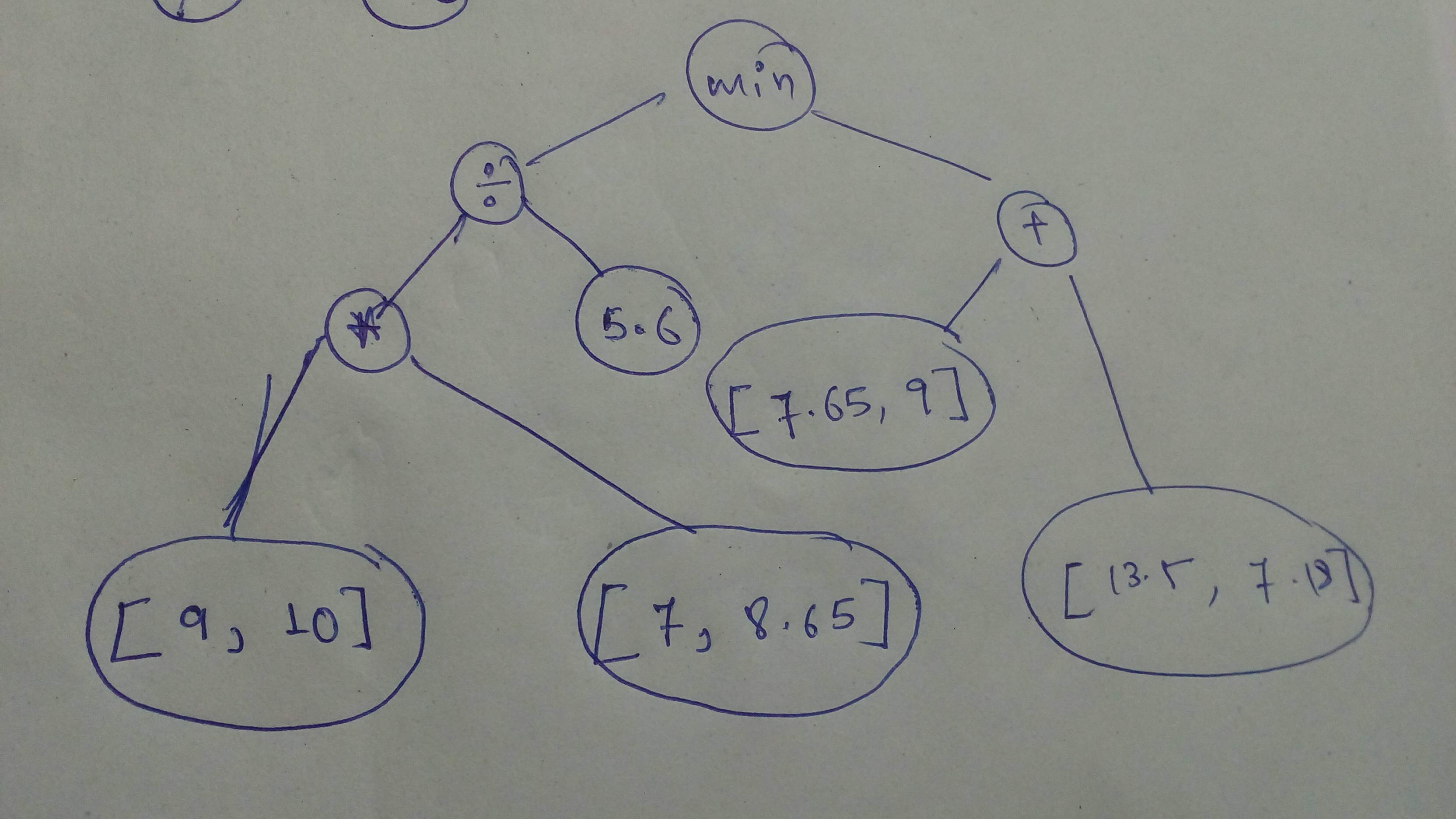\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "60b7e1a4-47ef-4d09-df03-ba9b890f325f"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "cg_1a=tf.cast(tf.multiply(tf.constant(([9,10]),dtype=tf.float32),tf.constant(([7,8.65]),dtype=tf.float32)),dtype=tf.float32)\n",
+ "cg_1b=tf.cast(tf.divide(cg_1a,5.6),dtype=tf.float32)\n",
+ "\n",
+ "cg_2=tf.cast(tf.add(tf.constant([7.65,9]),tf.constant([13.5,7.18])),dtype=tf.float32)\n",
+ "cg_3=tf.cast(tf.minimum(cg_1b,cg_2),dtype=tf.float32)\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess=tf.Session()\n",
+ "cg1,cg2,result=sess.run([cg_1b,cg_2,cg_3])\n",
+ "print(\"part 1\",cg1)\n",
+ "print(\"part 2\",cg2)\n",
+ "print(\"result\",result)\n",
+ "sess.close()"
+ ],
+ "execution_count": 113,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "part 1 [11.25 15.446429]\n",
+ "part 2 [21.15 16.18]\n",
+ "result [11.25 15.446429]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "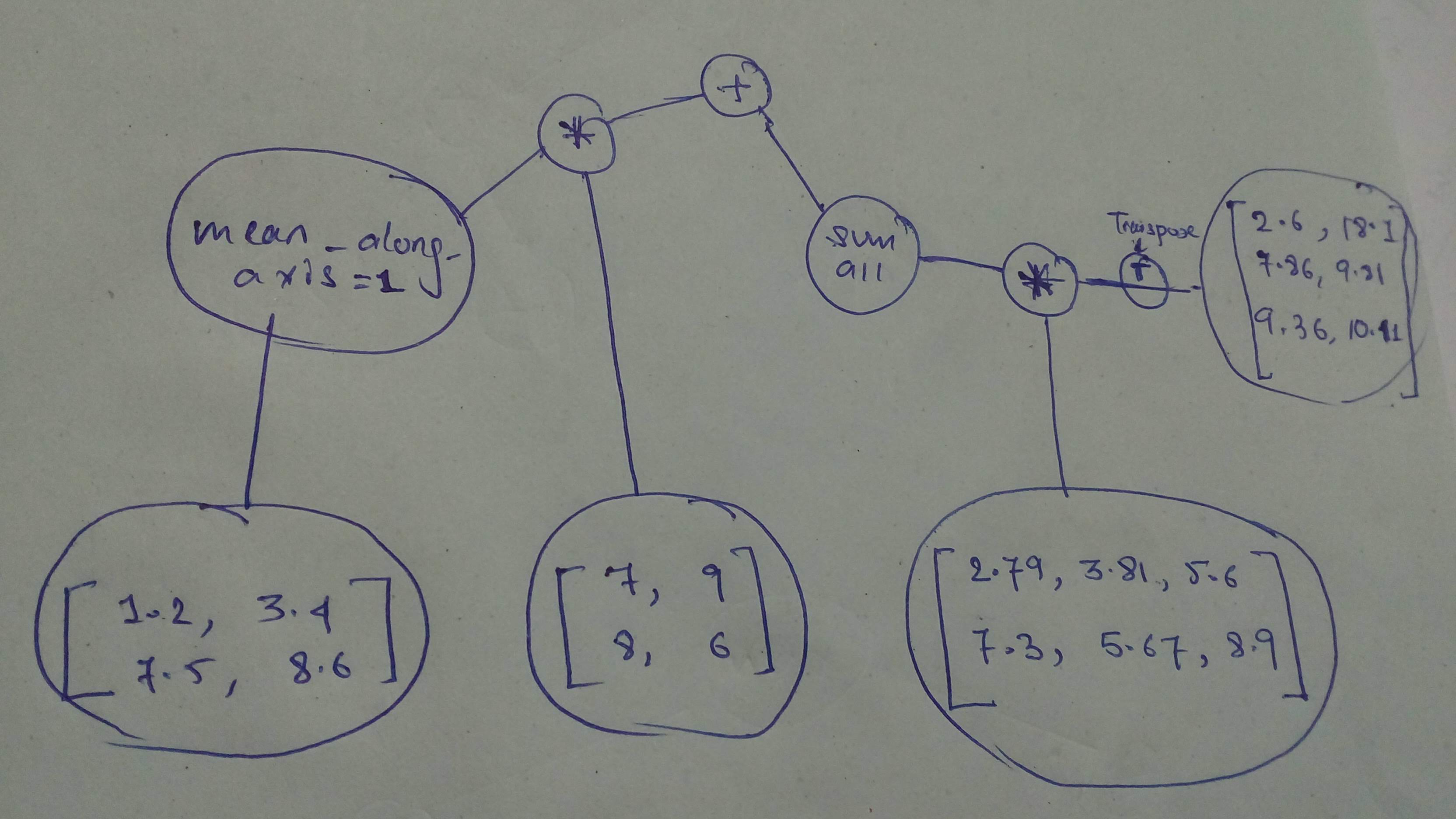"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 51
+ },
+ "outputId": "fd7e7d35-92b9-416f-aa01-dc87dde85595"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "cg_1a=tf.constant(([1.2,3.4],[7.5,8.6]),dtype=tf.float32)\n",
+ "cg_1b=tf.constant(([1.2,3.4],[7.5,8.6]),dtype=tf.float32)\n",
+ "cg_1=tf.reduce_mean(cg_1a, axis=1)*cg_1b\n",
+ "\n",
+ "cg_2a=tf.transpose(tf.constant(([2.6,18.1],[7.86,9.81],[9.36,10.41]),dtype=tf.float32)) * tf.constant(([2.79,3.81,5.6],[7.3,5.6,8.9]))\n",
+ "cg_2=tf.reduce_sum(cg_2a)\n",
+ "cg=cg_1 +cg_2\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess=tf.Session()\n",
+ "print(sess.run(cg))\n",
+ "sess.close()"
+ ],
+ "execution_count": 114,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[372.09158 396.70157]\n",
+ " [386.58157 438.56158]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ "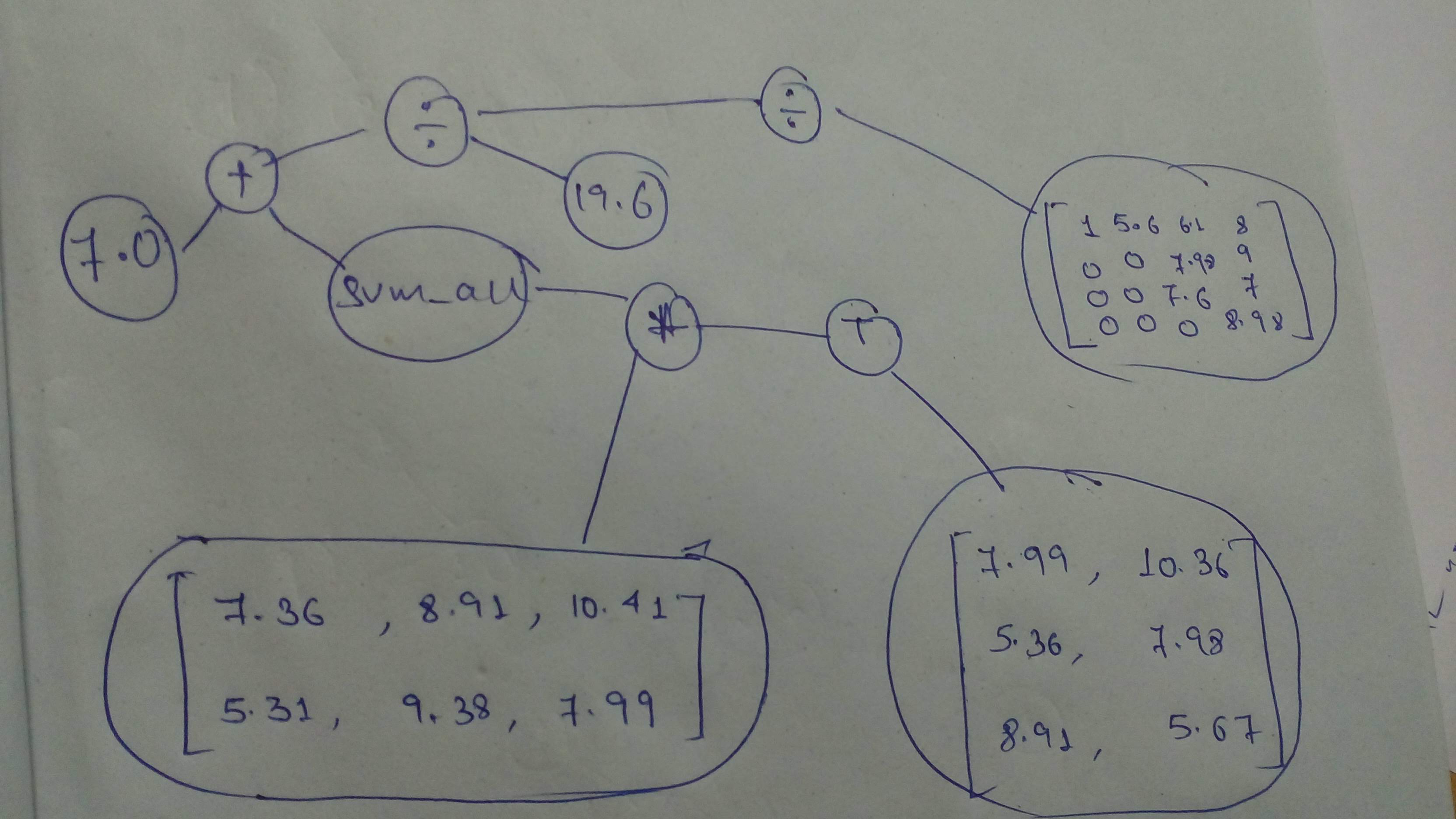"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 85
+ },
+ "outputId": "9058981e-dbd3-4a01-a5d6-04f8e4b1699b"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "cg1 = tf.constant(7.0, dtype = tf.float32)\n",
+ "cg2 = tf.constant([[7.36, 8.91, 10.41], [5.31, 9.38, 7.99]], dtype = tf.float32)\n",
+ "cg3 = tf.constant([[7.99, 10.36], [5.36, 7.98], [8.91, 5.67]], dtype = tf.float32)\n",
+ "cg4 = tf.constant([[1, 5.6, 6.1, 8], [0, 0, 7.98, 9], [0, 0, 7.6, 7], [0, 0, 0, 8.98]], dtype = tf.float32)\n",
+ "\n",
+ "cg_1 = (cg1 + tf.reduce_sum(cg2 * tf.transpose(cg3))) / 19.6\n",
+ "\n",
+ "cg = cg_1 / cg4\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess=tf.Session()\n",
+ "print(sess.run(cg))\n",
+ "sess.close()"
+ ],
+ "execution_count": 115,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[19.463488 3.475623 3.1907358 2.432936 ]\n",
+ " [ inf inf 2.4390335 2.1626098]\n",
+ " [ inf inf 2.5609853 2.7804983]\n",
+ " [ inf inf inf 2.1674263]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ },
+ "outputId": "23dd33e5-80b5-45a7-9f2c-33055d11a21b"
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'r')\n",
+ "plt.show()"
+ ],
+ "execution_count": 118,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFKCAYAAADmCN3IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3WlgVOXZxvH/LJlkspJggloBxQrU\nYlgCYoPYQout1FbflqBRUWpcEBQUVEJEAhVIXIIYwQURpZRFo1aRUrSvRaoFRYhvXLG2uBINCWSb\nTJKZZM77IZqasiQMk5zMzPX7NmfOOXPfHOCas8zzWAzDMBAREZGgZDW7ABEREfGfglxERCSIKchF\nRESCmIJcREQkiCnIRUREgpiCXEREJIjZzS7AH+XltQHfZ2JiNJWV7oDvtztTz+EhHHuG8OxbPYe2\n5OS4wy7XGfk37Hab2SV0OfUcHsKxZwjPvtVzeFKQi4iIBDEFuYiISBBTkIuIiAQxBbmIiEgQU5CL\niIgEMQW5iIhIEFOQi4iIBDEFuYiISBBTkIuIiAQxBbmIiEgQU5CLiIgEkPXrr4h8ej14PF3zeV3y\nKSIiIqHO5yPqiZUkjhpB/I3XY//gvS752KCc/UxERKQ7sX34AXGzphOxaye++ARq73uApsFDu+Sz\nFeQiIiL+qq8n+v57iV62FEtTEw0X/Ya6hfn4ep3YZSUoyEVERPwQ8fdXib3tZuyf7KX5lN647i7A\nM+4XXV6HglxEROQYWCoqiM3NIapoA4bVinvKjdTdngOxsabUoyAXERHpCMMg8ql1xM6/A+vBg3hT\nh+Aq6Lp74UeiIBcREWmHbe+/iL3tFhyvbcOIjsH1+8XUXzMF7ObHqPkViIiIdFceD9HLHyB6yT1Y\nGhtpHPdzXPkF+Hr3MbuyVgpyERGRw7DvfJO4W6dj3/MhzSm9cC2+B8+vLgaLxezS2lCQi4iIfIel\nuoqYhQtwrn4cgPqrsqibm4uR0MPkyg5PQS4iIgJgGDhefJ7YnNux7S+jacBAau8rpGnkOWZXdlQK\nchERCXvWL78gNnsWkS9vwYiMpG7OnbinzQCHw+zS2qUgFxGR8NXUhHPlI8TkL8LirsNz7nm47ltK\nc7/vm11ZhynIRUQkLNnf+T9iZ04n4p3/w5eURG3+fTReclm3e5itPQpyEREJLy4XMfcsxrniISw+\nHw0Zl+JasBjjhBPMrswvCnIREQkbjr9uIXb2LGxffkHzqadRe+9SvD8eY3ZZx0VBLiIiIc9SVkbs\n3NlEvfAcht1O3c234r7lNnA6zS7tuCnIRUQkdPl8RP1xNTG/n4e1phpv2ghqCwppPvOHZlcWMApy\nEREJSbaP9hA3azoRO9/AFxdPbX4BDZOzwGo1u7SAUpCLiEhoaWggeum9RD+4FIvXS+OFF+FafA++\nE08yu7JOoSAXEZGQEfH634m9dQb2vf+m+eTv4covwPOL8WaX1akU5CIiEvQsBw8QO38uURvWYlit\nuK+7AXf2XIzYOLNL63QKchERCV6GQWTRBmLnzcF64ADeQam4lhTSNGSY2ZV1GQW5iIgEJesne+Hy\n24j/618xoqNx5S6k/vqpYA+vaAuvbkVEJPh5vTgffpCY+/KhoYHGn47DdfcSfH36ml2ZKfwKcq/X\nS3Z2NqWlpdhsNvLy8ujdu3ebdTZu3Mjq1auxWq1MnDiRjIwM3G432dnZVFRU4HQ6yc/PJzk5mT17\n9jB//nwABgwYwIIFC467MRERCT32XTuJmzUD+4fv4zshGcuTT1Iz5oKgGx89kPz6Md2mTZuIj49n\n/fr1TJkyhYKCgjbvu91uli9fzpNPPsmaNWtYvXo1VVVVPP300/Tu3Zt169Zxww03UFhYCMCiRYvI\nyclhw4YNuFwutm3bdvydiYhIyLDU1hCbPYsevxyH/cP3qZ80mYPbd8Ell4R1iIOfQb5jxw7GjRsH\nQHp6OsXFxW3eLykp4ayzziIuLo6oqCiGDRtGcXExn376KampqQAMHz6c3bt34/F42LdvX+vyMWPG\nsGPHjuPpSUREQoVh4Ni0kcRRI3Cueozm759B1cYtuAoKMXokml1dt+BXkFdUVJCUlNSyA6sVi8WC\nx+M57PsASUlJlJeX079//9az7Z07d1JaWkplZSXx8fGt6/bs2ZPy8nK/mhERkRBiGMTMnU3C1Vdg\nPXiAuttzqPzbP/Cek252Zd1Ku/fIi4qKKCoqarOspKSkzWvDMI66j2/fnzBhAh999BGZmZmcffbZ\nbcK+o/sCSEyMxm63tbvesUpODv3fG/439RwewrFnCM++Q6Znw4DbboPHHoEf/hDLs88SM2AAMYdZ\nNWR69lO7QZ6RkUFGRkabZdnZ2ZSXlzNw4EC8Xi+GYeBwOFrfT0lJoaKiovX1/v37GTJkCA6Ho/VB\ntrq6Ol555RWSkpKoqqpqXbesrIyUlJSj1lRZ6e5Yd8cgOTmO8vLagO+3O1PP4SEce4bw7DuUeo7O\n+z0x9xfQdEZ/qp56ASMpBQ7TWyj13J4jfWHx69L6qFGj2LJlCwBbt25l5MiRbd4fPHgw7777LjU1\nNdTV1VFcXMzw4cPZtm0bS5cuBVqeah89ejQRERH069ePXbt2AfDyyy8zevRof8oSEZEQEF1wNzH3\n30fTaf2ofvZFjHZO7sKdXz8/Gz9+PNu3byczMxOHw0F+fj4AK1asYMSIEQwdOpRZs2aRlZWFxWJh\n2rRpxMXFMXLkSNauXcvEiRNJSEhgyZIlAOTk5DBv3jx8Ph+DBw8mPV33P0REwpHzwaXE3L2I5j59\nqX5uU8hOdBJIFqMjN6W7mc64jBJOl2e+pZ7DQzj2DOHZd7D37Hx0ObF3zqH55O9R9cJf8PU9td1t\ngr3nYxHQS+siIiKBFPXEypYQ73Ui1c+92KEQlxYKchERMVXUujXEzZ6J74Rkqp99keZ+3ze7pKCi\nIBcREdNEFm0g9pYb8SUmUvXMRpr7DzC7pKCjIBcREVNEvvAccTdNwYhPoLroBZrP/KHZJQUlBbmI\niHQ5x+ZNxE3JwoiOofqp52hKHWJ2SUFLQS4iIl3K8b8vEX/tVRAZRfX6Z2kaNtzskoKaglxERLpM\nxKt/I/53V4DdTvXap2kaeY7ZJQU9BbmIiHSJiO2vk3BVJgDVq9fjHaVRPAPBr5HdREREjoV955sk\nXJYBTU3UPLkW70/Gml1SyFCQi4hIp7K/vZuEzN9CYwM1K/+AZ9wvzC4ppCjIRUSk09jfLSFh4v9g\nqXNR++gqPL/8ldklhRwFuYiIdArbB++TkHERlppqapc9SuNFvzG7pJCkIBcRkYCzffxPekz4NdaD\nB6m9fxmNGZeaXVLI0lPrIiISUNa9/ybhNxdirSinNr+AhsuvNLukkKYgFxGRgLF+/hk9fvsrbGVf\n47orj4arrzW7pJCnIBcRkYCw7vuSHr+5ENu+L3HNXUD99dPMLiksKMhFROS4Wb/+ioTfXIjt88+o\nuz2H+um3mF1S2FCQi4jIcbGUl5Pw219h/2QvdTffinvWbLNLCisKchER8Zvl4AF6TPg19o//iXvK\njbjn3AkWi9llhRUFuYiI+MVSVUlCxsXYP3yf+qzrqFuwSCFuAgW5iIgcM0ttDQmX/oaId0uonzQZ\n16J7FOImUZCLiMixcblIyJxARPFuGi65DNe9S8GqODGL/uRFRKTj3G4SJl1CxM43aPif31K7dLlC\n3GT60xcRkY5paCDhqkwc/3iNxl/+mtplK8BmM7uqsKcgFxGR9nk8xGdNwrFtK40/v4CaR1dBRITZ\nVQkKchERaY/XS/x1vyPyry/hGfNTalb+ARwOs6uSbyjIRUTkyJqaiJt2LZGbX8Rz7nlUP7kOIiPN\nrkq+Q0EuIiKH19xM3IypRD3/HN6RP6J6zVPgdJpdlfwXBbmIiBzK5yP21hlEFW3Amzac6nVFEBNj\ndlVyGApyERFpyzCInXMrzrV/wDt4KNUbnsOIize7KjkCBbmIiPyHYRAzLwfnEytpOnMQ1U//CSOh\nh9lVyVEoyEVEpIVhELNoAdGPLqdpwECqntmIkZhkdlXSDgW5iIgAEH1vHtGFS2jqdzrVz2zEOOEE\ns0uSDlCQi4gIzgcKiLkvn+a+p1L93CZ8vU40uyTpILs/G3m9XrKzsyktLcVms5GXl0fv3r3brLNx\n40ZWr16N1Wpl4sSJZGRk4Ha7yc7OpqKiAqfTSX5+PsnJyUyaNAm32010dDQAs2fPZtCgQcffnYiI\ntMv58DJiFy2g+ZTeVD23Cd/J3zO7JDkGfgX5pk2biI+Pp6CggNdff52CggKWLl3a+r7b7Wb58uU8\n88wzREREMGHCBMaNG8fzzz9P7969KSwsZNeuXRQWFnLXXXcBkJeXR//+/QPTlYiIdEjU4yuIzc2h\n+aSTqXr2RXy9+5hdkhwjvy6t79ixg3HjxgGQnp5OcXFxm/dLSko466yziIuLIyoqimHDhlFcXMyn\nn35KamoqAMOHD2f37t3HWb6IiPgras2TxM25FV9yCtXPvojvtH5mlyR+8CvIKyoqSEpqeZLRarVi\nsVjweDyHfR8gKSmJ8vJy+vfvz7Zt2wDYuXMnpaWlresUFhZy+eWXM2/ePBoaGvxqRkREOiZyw1pi\nb52Br2dPqp59kebvn2F2SeKndi+tFxUVUVRU1GZZSUlJm9eGYRx1H9++P2HCBD766CMyMzM5++yz\nW8P+yiuvZMCAAfTp04fc3FzWrl1LVlbWEfeXmBiN3R74qfOSk+MCvs/uTj2Hh3DsGcKz7w71vGED\n3DwNevTA8sorJA0e3PmFdaJwPM7f1W6QZ2RkkJGR0WZZdnY25eXlDBw4EK/Xi2EYOL4zE05KSgoV\nFRWtr/fv38+QIUNwOBwsWLAAgLq6Ol555RWA1sv0AGPHjmXz5s1Hramy0t2B1o5NcnIc5eW1Ad9v\nd6aew0M49gzh2XdHenZs2kj8tVdhxMRS/dSfaDq5HwTxn1M4HecjfWHx69L6qFGj2LJlCwBbt25l\n5MiRbd4fPHgw7777LjU1NdTV1VFcXMzw4cPZtm1b60NxGzduZPTo0RiGweTJk6mpqQHgzTff5Iwz\ndIlHRCSgGhuJWvUY8df/DiPKSfWGZ2kaMszsqiQA/Hpqffz48Wzfvp3MzEwcDgf5+fkArFixghEj\nRjB06FBmzZpFVlYWFouFadOmERcXx8iRI1m7di0TJ04kISGBJUuWYLFYmDhxIpMnT8bpdNKrVy9u\nuummgDYpIhK2XC6ca57E+fCD2L7+CiM6hpp1RTSNGNn+thIULEZ7N7i7oc64jBJOl2e+pZ7DQzj2\nDOHZ93d7tlQexPn4CpyPPYy1shIjOob6yVnUT5mG78STTK40cMLpOB/p0rpfZ+QiItI9Wcu+xvnw\nMqJWr8Ja58KXmEjdbXOov+Z6jZseohTkIiIhwPrpJzDvYZKeeAJLYyPNvU7EdXsO9ZMmQ2ys2eVJ\nJ1KQi4gEMdueD4kuXELkn56B5mZ8fU/FfdMtNFxyGURGml2edAEFuYhIELIX7yJ6aQGRW/4MQNMP\nzsQ+9w4OjrkA7PqvPZzoaIuIBAvDIOL1vxO9tADHa68C4E0bjvvm2/CM+znJvRKC+jfh4h8FuYhI\nd+fz4XjpL0QXFhCxexcAnvPG4L55Ft5Ro8FiMblAMZOCXESku2pqIvL5Z4kuXIJ9z4cANI7/Fe4Z\nM2kammZycdJdKMhFRLqbhgainlpH9INLsX3+KYbNRkPGpbhvuoXmgT8wuzrpZhTkIiLdhMVVS9Tq\nJ1pGYdtfhhEZSf3vrsE9dTq+vqeaXZ50UwpyERGTWQ4ewLnyUZwrH8FaVYUvJhb3jTfjvn4aRq9e\nZpcn3ZyCXETEJNavv8L58DKcq1dhcdfhS0qibvYd1Gddh9Ej0ezyJEgoyEVEupj1k71EL3uAqKfW\nYvF4aD7pZOrnzKX+iskQE2N2eRJkFOQiIl3E9sH7LaOwPf8sFp+PptP6UX/TLTRkXKpR2MRvCnIR\nkU5m37WT6AcKiHzpLwA0nTkI982zaPzVxWCzmVydBDsFuYhIZzAMIv7+KtEPFOB4/e8AeEeMxH3z\nLDw/+7kGcZGAUZCLiASSz4fjL39uGYXt7WIAPGN+ivvmW/Gek64Al4BTkIuIBILXS+SfniH6wfux\nf7QHw2Kh8cKLWkZhGzzU7OokhCnIRUSOR0MDUev/SPTyB7B9/hmG3U7DpZe3jMJ2Rn+zq5MwoCAX\nEfGDxVVL1BOPE/3IMqzl+zGioqjPuq5lFLbefcwuT8KIglxE5FjU1+N8YiXRhQVYDx7EFxuHe/pM\n3NdNxUhJMbs6CUMKchGRjvB6Wy6hF9yN7atSfPEJLaOwXXM9RkIPs6uTMKYgFxE5Gp+PyD89Q8zd\ni7B9+gmG09lyBj5tOkZiktnViSjIRUQOyzBwvPQXYvLuwv7h+xgREdRffS3uW27D1+tEs6sTaaUg\nFxH5LxGvbSNm8QIidu/CsFppuOQy6m7N1lSi0i0pyEVEvmHf/RYxi+/C8dqrADReeBF1s++gecBA\ncwsTOQoFuYiEPduHHxCTdxeRW/4MtIzEVjfnTpqGDDO5MpH2KchFJGxZP9lLzL15RD77NBbDwHv2\nOdTlzMObfq7ZpYl0mIJcRMKO9atSopfcS9Ta1Viammj64VnU3TEPz0/P11joEnQU5CISNiwHDhD9\n4P04V63A0tBA0+nfx509t2U6UavV7PJE/KIgF5GQZ6mtwfnIcpwPL8PqqqX5e6fgvm0ODRMzwa7/\nBiW46W+wiISu/x5O9YQTcM2ZS/2k30FUlNnViQSEglxEQo/XC48+StL8Bdi+/qplONU5d+K+9gaI\njTW7OpGAUpCLSOhobm4ZTvWexfDpJ1g1nKqEAQW5iAS/1uFUf4/9ww8wIiLgxhs5eP10DacqIU9B\nLiJB7ZDhVC+9nLpbs+mZNghfea3Z5Yl0Or+C3Ov1kp2dTWlpKTabjby8PHr37t1mnerqambOnElM\nTAyFhYVH3W7Pnj3Mnz8fgAEDBrBgwYLj60pEQt5hh1PNnktz/wHmFibSxfz64eSmTZuIj49n/fr1\nTJkyhYKCgkPWyc3NJS0trUPbLVq0iJycHDZs2IDL5WLbtm3+lCUiYcD2wfvEX5lJ4gU/xfHaq3jG\n/JTKl1+lZtUahbiEJb+CfMeOHYwbNw6A9PR0iouLD1ln4cKFhwT54bbzeDzs27eP1NRUAMaMGcOO\nHTv8KUtEQpj1k73E3XANiWPSidzyZ7xnn0PV85upfupPGhNdwppfl9YrKipISmp5AtRqtWKxWPB4\nPDgcjtZ1Yg/zE4/DbVdRUUF8fHzrOj179qS8vNyfskQkBP33cKreQam4c+7UcKoi32g3yIuKiigq\nKmqzrKSkpM1rwzD8+vDDbdeRfSUmRmO32/z6zKNJTo4L+D67O/UcHoKy54oKuPtuWLYMGhqgf3+4\n6y4iJkwgoYPDqQZl38dJPYefdoM8IyODjIyMNsuys7MpLy9n4MCBeL1eDMNoczZ+JCkpKYdsl5yc\nTFVVVes6ZWVlpKSkHHU/lZXudj/rWCUnx1EeZk+4qufwEGw9tzuc6oG6Du0n2PoOBPUc2o70hcWv\ne+SjRo1iy5YtAGzdupWRI0f6vV1ERAT9+vVj165dALz88suMHj3an7JEJJjV1+N86EGSRqQSc28e\nREXiWnQ3B3cU03DZJI2JLnIEfv3LGD9+PNu3byczMxOHw0F+fj4AK1asYMSIEaSmpjJ58mRqamoo\nKytj0qRJTJ069Yjb5eTkMG/ePHw+H4MHDyY9PT1wHYpIt+f484vEzrlVw6mK+MFi+HuD20SdcRkl\nnC7PfEs9h4fu3rPtww9IHHce2GzUX3tDwIZT7e59dwb1HNqOdGld16pExDyNjcRPvRaLx0P1H5/C\nc/4FZlckEnT8ukcuIhIIMffmYX//XeqvuEohLuInBbmImML+5hs4ly2luc+p1P1+sdnliAQtBbmI\ndDmLq5b4G68DoGb5CozY8P4dsMjxUJCLSJeLyb0D22efUn/jzTSNPMfsckSCmoJcRLqU46W/4Fzz\nJE0/PIu623PMLkck6CnIRaTLWCoqiLvlRgyHg5qHHoMOjAgpIkenIBeRrmEYxN06A2tFOXU5uTT/\n4EyzKxIJCQpyEekSkU+tI3Lzi3jSz6V+yjSzyxEJGQpyEel01s8/IzbndnyxcdQ++Ah0cPYyEWmf\nRnYTkc7l8xE3/QasrlpqCh/G17uP2RWJhBR9LRaRTuV8ZDmO7a/TeMGFNF5ymdnliIQcBbmIdBrb\nhx8Qs3gBvhOSqS0oBIvF7JJEQo6CXEQ6x3cmRKldugzjhBPMrkgkJCnIRaRTaEIUka6hIBeRgNOE\nKCJdR0EuIgGlCVFEupaCXEQCShOiiHQtBbmIBIzjZU2IItLVFOQiEhCWigribtaEKCJdTUEuIsfv\nuxOizJmnCVFEupCCXESOmyZEETGPglxEjsshE6LYbGaXJBJWNGmKiPhPE6KImE5n5CLiN02IImI+\nBbmI+EUTooh0DwpyETl2Ho8mRBHpJhTkInLMNCGKSPehIBeRY2J/8w2cD96vCVFEugkFuYh0WOuE\nKIZBzbJHNSGKSDegIBeRDmudEOWmW2g650dmlyMiKMhFpIM0IYpI96QgF5F2aUIUke5LQS4iR6cJ\nUUS6NQW5iByVJkQR6d78Gmvd6/WSnZ1NaWkpNpuNvLw8evfu3Wad6upqZs6cSUxMDIWFhUfdbtKk\nSbjdbqKjowGYPXs2gwYNOs7WROR4aUIUke7PrzPyTZs2ER8fz/r165kyZQoFBQWHrJObm0taWlqH\nt8vLy2PNmjWsWbNGIS7SHXxnQhTX4ns0IYpIN+VXkO/YsYNx48YBkJ6eTnFx8SHrLFy48JAg78h2\nItI9aEIUkeDg16X1iooKkpKSALBarVgsFjweD47vPMkaGxvb4e0ACgsLqays5PTTTycnJ4eoqKgj\nfn5iYjR2e+Av8SUnh9/gFuo5PBxzz++9B4sXQEoKkatXkZwc3zmFdTId6/AQjj1/V7tBXlRURFFR\nUZtlJSUlbV4bhuHXh3+73ZVXXsmAAQPo06cPubm5rF27lqysrCNuV1np9uvzjiY5OY7y8tqA77c7\nU8/h4Zh79nhIvPQy7B4P1QUP4iEKgvDPTMc6PIRTz0f6wtJukGdkZJCRkdFmWXZ2NuXl5QwcOBCv\n14thGG3Oxo8kJSXlsNt9e7kdYOzYsWzevLndfYlI52gzIcrPNSGKSHfn1z3yUaNGsWXLFgC2bt3K\nyJEj/d7OMAwmT55MTU0NAG+++SZnnHGGP2WJyHHShCgiwceve+Tjx49n+/btZGZm4nA4yM/PB2DF\nihWMGDGC1NTU1nAuKytj0qRJTJ069bDbWSwWJk6cyOTJk3E6nfTq1YubbropoE2KSPs0IYpIcLIY\n/t7gNlFn3A8Jp/ss31LP4aGjPcfOmo5zzZO4p8+kbu78zi+sk+lYh4dw6vlI98g1spuIaEIUkSCm\nIBcJc5oQRSS4KchFwpkmRBEJegpykTCmCVFEgp+CXCRMWb/4XBOiiIQAv35+JiJBzucj7qYpWF21\n1BQ+rAlRRIKYzshFwpAmRBEJHQpykTBj+/ADYhYvwHdCMrUFhWCxmF2SiBwHBblIOPF4iJ96LRaP\nh9r7l2GccILZFYnIcVKQi4QRTYgiEnoU5CJhQhOiiIQmBblIGNCEKCKhS0EuEgZicu/A9tmn1N90\nC03n/MjsckQkgBTkIqFu0yZNiCISwhTkIiHMUlEB11yjCVFEQpiCXCRUfTMhCmVlmhBFJIQpyEVC\n1LcTonDeeZoQRSSEKchFQtB3J0Rh9WpNiCISwhTkIqHmOxOiuBbfA6eeanZFItKJNPuZSChpaCB6\n6b2aEEUkjCjIRYKdYWDftZOop9YT+cJzWKurNCGKSBhRkIsEKesXnxNVtIHIp9dj3/tvAJpPPAn3\nlb+j/qqrNSGKSJhQkIsEE5eLyE0vEPX0ehyv/x0Aw+mk4TcZNFxyGd7zfqIH20TCjIJcpLvz+Yh4\n/e9EPbWOyD9vxOJ2A+D50SgaL7mMxl9dhBEXb3KRImIWBblIN2X718ct4f3MU9j2fQlAc99TaZiY\nSUPGpfhOPc3kCkWkO1CQi3QjlsqDRD7/HFFPryNi9y4AfHHx1F9xFQ0TL6Np5Dl6gE1E2lCQi5jN\n68Xxt/9tue/90mYsHg+G1YpnzE9puOQyGi+4EJxOs6sUkW5KQS5iEtu77xD19Dqini3CWlEOQNPA\nH9Aw8TIaJ0zEd+JJJlcoIsFAQS7ShSxlZUQ9+zRRT6/H/sF7APiSknBfcz2Nl1xGU+oQXToXkWOi\nIBfpbA0NRL60mcin1uHY+gqW5maMiAgax/+KhomZeH52vqYXFRG/KchFOoNhYH9rZ8tT5y88h7Wm\nGgDvkKEt970vnoDRs6fJRYpIKFCQiwTQ0UZba7jkMpoHDDS5QhEJNQpykeNkcdXi2LSRqKfW4fjH\na4BGWxORrqMgF/FHc3PLaGtPr2872to56S2jrf36Yo22JiJdwq8g93q9ZGdnU1pais1mIy8vj969\ne7dZp7q6mpkzZxITE0NhYWHr8p07dzJjxgwWL17MmDFjANizZw/z588HYMCAASxYsMDPdkQ6V+to\na0UbsJXuAzTamoiYy+rPRps2bSI+Pp7169czZcoUCgoKDlknNzeXtLS0Nss+//xznnjiCYYNG9Zm\n+aJFi8jJyWHDhg24XC62bdvmT1kincJSeZCoVY/R44KxJKWnEf1AAZaaGuovv5KqjVs4uLME921z\nFOIiYgq/gnzHjh2MGzcOgPT0dIqLiw9ZZ+HChYcEeXJyMsuWLSMuLq51mcfjYd++faSmpgIwZswY\nduzY4U9ZIgFl/aqUuKnX0vOs/sRlz8L+djGeMT+l5pHHOfDex7juX4b3nHT97ltETOXXpfWKigqS\nkpIAsFqtWCwWPB4Pju/8FjY2NvaQ7ZyHGWaysrKS+Pj/3Evs2bMn5eXl/pQlEhjNzUQ98Rgxi+/C\n6qqlqf8AGi65nMaMSzTamoh0O+0GeVFREUVFRW2WlZSUtHltGEbACurIvhITo7HbA/8UcHJyXPsr\nhRj1/F+Ki+H662HXLujRA1bAnJkbAAAS/0lEQVSswJ6VRazVyqFfTYNHOB5nCM++1XP4aTfIMzIy\nyMjIaLMsOzub8vJyBg4ciNfrxTCMNmfjxyIpKYmqqqrW12VlZaSkpBx1m8pKt1+fdTTJyXGUl9cG\nfL/dmXr+D4urlui7F+F87BEsPh8Nv52Ia8FijJQUOFBnQqWBE47HGcKzb/Uc2o70hcWve+SjRo1i\ny5YtAGzdupWRI0f6XVhERAT9+vVj166WKRtffvllRo8e7ff+RI6VY/MmEs89m+hHH6K576lUPf08\ntQ+vbAlxEZFuzq975OPHj2f79u1kZmbicDjIz88HYMWKFYwYMYLU1FQmT55MTU0NZWVlTJo0ialT\np9LY2Mjjjz/O3r17ef/991mzZg2rVq0iJyeHefPm4fP5GDx4MOnp6QFtUuRwrPu+JHbObURu+TNG\nRAR1M2/DPeNWTRkqIkHFYgTyBncX6YzLKOF0eeZbYdvzV5U4Vz5CTP4iLO46PD8ahevepTT3H2B2\neZ0iHI8zhGff6jm0HenSukZ2k/Dy1lv0yLqWiHdL8CUmUpt3L42XXq6fkIlI0FKQS1iw1NYQs/j3\nsOoxIgyDhksuw5W7EOOEE8wuTUTkuCjIJbQZBo5NLxB7x2xsX38F/ftTlb8E77nnmV2ZiEhA+PXU\nukgwsH7+GfFXTCQh60qsBw9Qd3sOvPOOQlxEQorOyCX0eL04H32ImPvysLjdeEb/GNc9S2g+/Qxi\nIiMBj9kViogEjIJcQor9rTeJu/Vm7B++j69nT2rvuZ/GjEv1MJuIhCwFuYQES3UVMQsXEPWHVVgM\ng/orrqLuzgUYiUlmlyYi0qkU5BLcDIPI558ldm421vL9NA0YiOvepS2zkomIhAEFuQQt6yd7iZs9\nE8erf8OIiqIuZx7uqdPBz3H/RUSCkYJcgo/HQ/RDhUQvuQdLQwOen4yl9u4l+E7rZ3ZlIiJdTkEu\nQcX+xg7ibpuB/aM9+JJTqH3gIRov/q0eZhORsKUgl6BgqTxIzF25OP+4GoD6q7Kom5uLkdDD5MpE\nRMylIJfuzTCIfOYpYnNzsFZU0PSDH1J731KaRvg/da6ISChRkEu3Zfv3x8TePgvHa69iOJ245t1F\n/fVTISLC7NJERLoNBbl0P42NRD94P9EPFGBpbKTxZ+fjyi/A16ev2ZWJiHQ7CnLpViL+8Rqxt92M\n/V8f09zrRFyL78Fz4UV6mE1E5AgU5NItWA4cIHb+HUQ9tQ7DYqE+6zrq5tyJEZ9gdmkiIt2aglzM\nZRhEblhL7IK5WA8exDsoFdd9S2kaNtzsykREgoKCXExj+/ifxN52M47tr2NEx+D6/WLqr5kCdv21\nFBHpKP2PKV2voYHopfcR/eD9WLxeGn/xS1yL78F3Sm+zKxMRCToKculSEdu2Env7Ldg/2Uvzyd/D\ntfhePOMvNLssEZGgpSCXzuX1Yv/gPezFu3G8+jci/7IJw2rFff003LNzMGLjzK5QRCSoKcglcAwD\n62efElG8C/vbu4nYvQv7e+9gaWhoXcU7ZCiu+x6gKXWIiYWKiIQOBbn4zVJ5sCWwi3djL95FxNu7\nsR440Pq+YbPRdOYgmoam4U0bTtPQNJr7DwCr1cSqRURCi4JcOqaxEft777ScbX8T3PZP9rZZpblP\nXxrO/TFNw4bjHTacprNSITrapIJFRMKDglwO5fNh++Tf2Hfvar1Mbn/vXSxe739WSeiB5ydj8Q5L\nawnuIWkYKSkmFi0iEp4U5IKlvJyIt3e1XB4v3o397WKs1VWt7xsRETQNOqslsIem0ZQ2nObTTtcl\nchGRbkBBHm7cbuzvlBDx9m54//9IeuNNbJ9/1maVpn6n4/nZ+a33tZsGpUJkpEkFi4jI0SjIQ1lz\nM7aP//mfJ8jf3o39g/ewNDe3rmLp2ZPGn53/zX3tNJqGpmEkJplYtIiIHAsFeQixfv1Vy33tt795\nGO3/3sbqqm1934iK+k9gDxtO/M9+zIHYEzSzmIhIEFOQByuXi4iSt9sEt+2r0jarNPUfgOc797Wb\nfvBDiIj4zwrJcVBei4iIBC8FebAxDKLWPEnsvDlY3O7Wxc0pvWj8xS9pGpbW8tOvIUM1BaiISBhQ\nkAcRy8EDxM2cTuTmF/H16EH95GtaHkgbNhzfyd/TJXIRkTCkIA8SEa//nbhp12H7qhRP+rnULl+B\n73unmF2WiIiYTD8E7u68XmIWLSDht7/Cur+Mupx5VD/7okJcREQAP8/IvV4v2dnZlJaWYrPZyMvL\no3fvtnNJV1dXM3PmTGJiYigsLGxdvnPnTmbMmMHixYsZM2YMAJMmTcLtdhP9zXCes2fPZtCgQf72\nFDKse/9N/A1ZRLxdTHPfU6l55HGa0kaYXZaIiHQjfgX5pk2biI+Pp6CggNdff52CggKWLl3aZp3c\n3FzS0tLYs2dP67LPP/+cJ554gmHDhh2yz7y8PPr37+9POaHHMIh8ah2xc27DWueiIeNSXPn3YcTF\nm12ZiIh0M35dWt+xYwfjxo0DID09neLi4kPWWbhwIWlpaW2WJScns2zZMuLiNAf1kViqq4ibcjXx\n028Aq5Wah1dSu3yFQlxERA7LrzPyiooKkpJaRv+yWq1YLBY8Hg8Oh6N1ndjY2EO2czqdR9xnYWEh\nlZWVnH766eTk5BAVFXXEdRMTo7Hbbf6UflTJySZ/wfjHP+Dyy+Gzz+Ccc7CuW0f8aad16kea3rMJ\n1HP4CMe+1XP4aTfIi4qKKCoqarOspKSkzWvDMI6riCuvvJIBAwbQp08fcnNzWbt2LVlZWUdcv7LS\nfcT3/JWcHEe5WYOjNDURff+9RBfcDYB75u24b80Gu71TB2wxtWeTqOfwEY59q+fQdqQvLO0GeUZG\nBhkZGW2WZWdnU15ezsCBA/F6vRiG0eZs/Fh9e5keYOzYsWzevNnvfQUb6xefE3/DNUTsfIPm751C\n7cMr8Z6TbnZZIiISJPy6Rz5q1Ci2bNkCwNatWxk5cqTfBRiGweTJk6mpqQHgzTff5IwzzvB7f8Ek\n8k/PkDhmFBE736Dh1/9D5dZ/KMRFROSY+HWPfPz48Wzfvp3MzEwcDgf5+fkArFixghEjRpCamtoa\nzmVlZUyaNImpU6fS2NjI448/zt69e3n//fdZs2YNq1atYuLEiUyePBmn00mvXr246aabAtpkd2Nx\n1RKbcztRG9ZiRMdQ88BDNF56uUZmExGRY2YxjvcGtwk6435IV91nsb+9m7gpWdg/2Yt38FBqH1lJ\n8+nmXIEIp3tL31LP4SMc+1bPoe1I98g1sltX8flwFt5Pj1+Ow/7JXtw33kzVn/9qWoiLiEho0Fjr\nXcD6VSlxN16P47VtNPc6kdplj+L98RizyxIRkRCgM/JO5ti8icSf/AjHa9to/MV4Kl/doRAXEZGA\n0Rl5Z3G7iZ2Xg/MPqzCioqi9ewkNk7P0QJuIiASUgrwT2N59h/gbsrD/8yOazhxEzSOP0zzwB2aX\nJSIiIUiX1gPJ58P56HISLxiL/Z8f4b7uBiq3/E0hLiIinUZn5AFi2b+f+OlTcPztf/GdkExN4UN4\nfvZzs8sSEZEQpyAPAMf/vkTc9KlYK8rxjP0ZNYWPYKSkmF2WiIiEAV1aPx4NDcTMnU3CZRlYaqpx\n3ZVH9bpnFOIiItJldEbuJ9tHe4i//mrsH7xHU/8B1Dz8OM1npZpdloiIhBmdkR8rwyDqiZUkjjsP\n+wfvUX9VFpUvb1OIi4iIKXRGfgwsBw4Qd8s0IrdsxpeYSM0jq/CMv9DsskREJIwpyDso4u+vEjft\nOmxlX+M59zxql6/Ad9LJZpclIiJhTpfW2+PxEPP7eSRkXIT1QAWuuQuoLnpBIS4iIt2CzsiPwvbv\nj4mbcg0RJW/TdFo/ah95nKahaWaXJSIi0kpn5IdjGESu/yOJPz2PiJK3abj0cqpeeU0hLiIi3Y7O\nyP+LpaqS2NtuIeqF5/DFJ1D76Coa/2eC2WWJiIgcloL8OyLe2E7c1GuxffkF3rPPoeahx/D16Wt2\nWSIiIkekS+sATU2Qm0vCxeOxlu6j7rY5VD2/WSEuIiLdns7I6+vpkXER7HwDX+8+1Dy0kqaR55hd\nlYiISIeE/Rm5dX8Z9vfegcxMKv/2ukJcRESCStifkfv6nkrFx1+QfHISRnmt2eWIiIgck7A/Iwcg\nIsLsCkRERPyiIBcREQliCnIREZEgpiAXEREJYgpyERGRIKYgFxERCWIKchERkSCmIBcREQliCnIR\nEZEgpiAXEREJYgpyERGRIKYgFxERCWIWwzAMs4sQERER/+iMXEREJIgpyEVERIKYglxERCSIKchF\nRESCmIJcREQkiCnIRUREgpjd7AI6m9frJTs7m9LSUmw2G3l5efTu3bvNOtXV1cycOZOYmBgKCwuP\nut2ePXuYP38+AAMGDGDBggVd3VK7OtLzxo0bWb16NVarlYkTJ5KRkYHb7SY7O5uKigqcTif5+fkk\nJyczadIk3G430dHRAMyePZtBgwaZ0doRBbrnUD7OZWVl5OTk4PF48Pl8zJkzh0GDBjF27FhOPPFE\nbDYbAPfddx+9evUyo7WjCnTf27dvZ8mSJdhsNs477zymTZtmUmdH5m/PDz/8MNu3bwfA5/NRUVHB\nSy+9FBTHOtA9B8Nx9psR4p577jlj/vz5hmEYxmuvvWbMmDHjkHVmzJhhLF++3Ljpppva3e6KK64w\nSkpKDMMwjJkzZxqvvvpqZ7dwzNrrua6uzjj//PONmpoao76+3vjlL39pVFZWGk888YRxzz33GIZh\nGG+99ZYxd+5cwzBaev7oo4+6tolj1Bk9h+pxzs/PN9avX28YhmHs3r3buPrqqw3DMIwxY8YYLper\na5vwQ6D7vuCCC4zS0lKjubnZyMzMND7++OOubagD/O35v/fx2GOPGYYRHMc60D0Hw3H2V8hfWt+x\nYwfjxo0DID09neLi4kPWWbhwIWlpae1u5/F42LdvH6mpqQCMGTOGHTt2dHIHx669nktKSjjrrLOI\ni4sjKiqKYcOGUVxczKefftra2/Dhw9m9e3eX1+6vQPYc6sc5MTGRqqoqAGpqakhMTOzy2o9HIPv+\n4osvSEhI4KSTTsJqtfLjH/84pI71t5qamli/fj1XXHFFl9Z9PALZc7AcZ3+F/KX1iooKkpKSALBa\nrVgsFjweDw6Ho3Wd2NjYDm1XUVFBfHx86zo9e/akvLy8kzs4du31/N33AZKSkigvL6d///5s27aN\nn//85+zcuZPS0tLWdQoLC6msrOT0008nJyeHqKiorm2qHYHsubKyMqSP8+TJk5kwYQLPP/88LpeL\n9evXt66Tm5vLvn37SEtLY9asWVgslq5tqgMC2Xd5efkh637xxRdd21AH+Nvzt15++WXOPffcNv9u\nu/uxDmTPwXKc/RVSQV5UVERRUVGbZSUlJW1eG36OSHu47fzdVyAFoudv358wYQIfffQRmZmZnH32\n2a1/8a+88koGDBhAnz59yM3NZe3atWRlZQWwi2PTFT0fy766QiB7XrlyJRdccAE33HADW7du5e67\n72bZsmVMnz6d0aNHk5CQwLRp03jppZf4xS9+EdhGjlFn93311VcHtuAACGTP33r22WfbPOfR3Y51\nV/QcykIqyDMyMsjIyGizLDs7m/LycgYOHIjX68UwjDZn40eSkpJyyHbJycmtl+YAysrKSElJCXgf\nx8KfnlNSUqioqGh9vX//foYMGYLD4Wj9i19XV8crr7wC0Hp5C2Ds2LFs3ry5M1tqV2f3nJSUFNLH\n+a9//Ss333wzAKNGjWrt/+KLL25d97zzzuOf//yn6UHe2X3/97qhdqwB3G43X3/9Naecckrr+93t\nWHd2z93xOAdSyN8jHzVqFFu2bAFg69atjBw50u/tIiIi6NevH7t27QJaLt2MHj26cwo/Du31PHjw\nYN59911qamqoq6ujuLiY4cOHs23bNpYuXQq0PA06evRoDMNg8uTJ1NTUAPDmm29yxhlndG1DHRDI\nnkP9OPft27f1bOedd96hb9++1NbWkpWVhcfjAeCtt97qlscZAtv3Kaecgsvl4ssvv6SpqYmtW7cy\natSoLu+pPf72DLBnzx769evXum6wHOtA9hwsx9lfIT/7WXNzM3PnzuXTTz/F4XCQn5/PSSedxIoV\nKxgxYgSpqamtQVVWVsYZZ5zB1KlTOfvssw+73b/+9S/mzZuHz+dj8ODBzJkzx+wWD9Fez0OHDmXL\nli08/vjjWCwWrrjiCn7961/T0NDA9OnTqaqqIiEhgSVLlhAXF8fmzZtZuXIlTqeTXr16sWjRIpxO\np9ltthHonkP5OO/fv5877riDhoYGAO644w4GDhzI6tWref7554mMjOTMM8/kzjvv7Hb3TSHwfb/1\n1lvcd999AJx//vmm3jY6En97Blp/evXdy8zBcKwD3XMwHGd/hXyQi4iIhLKQv7QuIiISyhTkIiIi\nQUxBLiIiEsQU5CIiIkFMQS4iIhLEFOQiIiJBTEEuIiISxBTkIiIiQez/AROiYbAsVAK9AAAAAElF\nTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 432
+ },
+ "outputId": "b74563f6-3e06-40ce-bb90-67f7d7013447"
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 123,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07239858\n",
+ "Loss after epoch 20 is 0.07236038\n",
+ "Loss after epoch 40 is 0.0723222\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.015346773\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XlYlPX6x/H3LCwiqKCACpqKioqy\nqJlLrmmW1alfpzpWpqWttp9KixZbPVZqWZ06ZbZb2mLn2GZl2aq5g4I7brgCisiAwCzP7w9wlFJx\nAR4YPq/r8spxvjPct6if5lnur8UwDAMRERGpMaxmFyAiIiLlKZxFRERqGIWziIhIDaNwFhERqWEU\nziIiIjWMwllERKSGsZtdwGHZ2fmmfv3Q0CBycwtNraEq+Xp/4Ps9qr/azdf7A9/vsbL7Cw8POe5z\n+uRcxm63mV1ClfL1/sD3e1R/tZuv9we+32N19qdwFhERqWEUziIiIjWMwllERKSGUTiLiIjUMApn\nERGRGkbhLCIiUsMonEVERGqYGjOEpCZ6+eUXWL9+Lfv376OoqIjmzaNo0KAhEyc+Xynvf8UVlxAR\nEYnVeuT/kV555Y0zft/ffvuZc87pzcGDecyY8Trjxj18xu8pIiLV56TCecOGDYwdO5brr7+eESNG\nlHtu4cKFTJ06FZvNRr9+/bj99tsBmDhxIqmpqVgsFpKTk4mPj6/86qvYnXfeC8DXX3/B5s0Z3HHH\nPZX+NSZPfomgoKBKfc9Zs2bStevZNG7cRMEsIlILVRjOhYWFPPXUU/Tq1euYzz/99NPMmDGDyMhI\nRowYwdChQ9m/fz/btm1j9uzZZGRkkJyczOzZsyu9eLOsWLGMWbM+oLCwkDvuuJf77ruDr776AYBH\nHhnH5ZdfRYcOHZk48Qny8/Nxu93cc88DtG3b7qTe/6KLzvvL+61cuZyCAgfbt29j584d3HXXffTq\n1Yd5877i009nY7FYGD78WpxOJ2vWpHH//Xfx4IOP8sQTjzBjxvssXryY556bjN1uJzw8goceeoz5\n879l1aoUDhzIZfv2bVxzzXVcfPFlVfb7JiIiJ6fCcPb392f69OlMnz79L89lZmbSsGFDmjVrBkD/\n/v1ZtGgR+/fvZ/DgwQDExMSQl5eHw+EgODj4tAt9fOEjfJHx39N+/bFcEnMZj/d++rRem5GxiY8+\nmoO/v/8xn//4448455zeXHLJZWzZsplp0ybz4ouvnkm5ZGXtZfLkl/jjj4X873+fkZCQyDvvvMm7\n735ESYmTZ56ZwKRJU3nzzf8wefJL5OUd8L52woQJTJ78MpGRTZk69Vm+/34eFouFjIxN/Oc/b7Fj\nRyYTJiQrnEVE/sTpdvLdtnkkuDoSbW9bLV+zwnC22+3Y7cdelp2dTVhYmPdxWFgYmZmZ5ObmEhcX\nV+7Xs7OzTxjOoaFBJ5xbGlTPH6vVUlG5pySonn+5wePHG0IeEhJIUNCRtY0aBdGpU0eiohoDYLFY\nvM8FBPjRqFEQ69ens3//fhYs+A6A4uJDf3l/m83KQw/di81W2ndoaCgvvfTSMd+vfv0AevU6h/Dw\nEGJjW1NcfIi8vCzatWtLdHQ4ADNmTPe+b5MmwdhsTux2K35+biwWC507l35yHzCgL0uXLqVTp06c\nfXY3mjZtREiIH4cOFZxwEHttUNvrr4j6q918vT/wrR4dJQ5mrJjB1D+msj1vO8PaDeOra76qlq9d\nLReEGYZR4ZqKdvoYl/QY45Ieq6ySvA7vhhUeHnLcnbHy84soLCzxPn/gQCGGYfE+NgzD+/OCgkPe\n5++88z46dz5yrv3P7+92e/jXv14od845Ozv/mO9XUFCMn189srPzyc0toKTERV5eEUVFJcd835wc\nB3l5BbhcHvbtKyj3nvv2HaSoyEV+fhElJR6ys/MpLCzE7faYvjvYmTjR99AXqL/azdf7A9/pMbsw\nmxmr/8NbadM5UHyAevZ63NjlFp4Y8lil9ldlu1JFRESQk5Pjfbx3714iIiL+8utZWVmEh4efyZeq\n0SwWC0VFRRQVFbFhw3oAOnXqzC+//ATAli2bmTXrgzN6v2M566xWbN++jcLCQoqLi7nnnrEYhoHF\nYsXtdnvXNWjQAIvFwp49ewBISVlBhw4dT6NTERHftTkvgwd+vpdu78cxdfnz2Cw2xp2dzIrr1jCx\n7/M0D2lebbWc0Sfn6OhoHA4HO3bsoGnTpixYsIDJkyeTm5vLyy+/zPDhw0lPTyciIuKMzjfXdJdd\ndgU33zyKVq3aEBtbGnpXXPEPnnnmccaOvRGPx8M999x/Ru93LPXq1WPMmFu5556xAPzjH9dgsVhI\nSurK2LFjePjhx71rn3rqKZ544mFsNhtRUdGcd975fPfdN6fXsIiIDzlQlMsDP9/L3IzPMTBo2aAV\nYxPvZHjstQT5Ve7dNCfLYlRwzDktLY1nn32WnTt3YrfbiYyMZNCgQURHRzNkyBCWLl3K5MmTATj/\n/PMZM2YMAJMnT2bZsmVYLBYmTJhAhw4dTliI2YdCfOVwzPH4en/g+z2qv9rN1/uD2tljXvEBrpx7\nKSnZK+nSJIE7k+7h4phLsVv/+tm1svs70WHtCsO5upj9Da2Nf6hOha/3B77fo/qr3Xy9P6h9PeaX\nHOSqLy5j+d5lDO9wLS8O/DdWy/HP9lZnOGt8p4iI1DmOknyGf/l3lu9dxpXth/PCgFdOGMzVreZU\nIiIiUg0cTgdXf3UFS/cs5vJ2V/LSoNewWY9/K68ZFM4iIlJnFDgLGPHVVSzevYhLYy7nlfNer3HB\nDApnERGpIwqdhYz8ejgLd/3GxW0u5dXB04954VdNoHAWERGfV+QqYtQ3V/Przp8Z1voSXh/yFn42\nP7PLOq6a+b8MNcTu3bsYOXI4sbGlt4GVlJRw7bWj6N9/4Cm/12efzebAgQP06zeAX375iTFjbjnm\nusPbPfr5VfyHZvPmTUyd+txftpns3/8cunRJ8D5u3Lgxr776yinX/GcLFsxn4MDBbNy4/oQ9iIjU\nFI6SfHYX7ObR3x/k5x0LGNrqQt44/+0aHcygcK5Qy5ZnecPv4ME8brjhWnr27EVAQOBpvV+7drG0\naxd73OcPb/d4MuF8PMHBwZWyL/SfffDBuwwcOLjCHkREqtPG3A38lPkDuwt2s6fcjz04nEdufRrc\n8nzeHPoe/rZjb1hUkyicT0GDBg1p3LgJ+/bt4+23p2O3+3Hw4AGefHISzz33DLt27cTlcnHjjbfS\nrdvZLFu2hJdemkJYWGMaN25C8+ZRrFixjDlzPubpp5874XaP06a9xty5nzN//jwsFit9+w7g6qtH\nkJW1l0cffRA/Pz/atm1/0rXv2LGDsWPvYMaM9wEYM+Y6nn76Wd566w2aNAln/fq17N27h8cee5rY\n2A7MnPkuP/30AxaLlVtvvYN169awadMGkpMf4Ior/uHt4Ycfvmf27JnYbDZiYztyzz33M2PG68fc\n3lJEpDIZhsG76W/xyG/jKfGUlHuucWBjzmrQiqb1m9KsfnPahrZndOebCLAFmFTtqak14Vz/8UcI\n+KJyt4wsvuQyCh4/+S0jd+/excGDeURERAKlM6vHj3+YefO+onHjJjz00GMcOHCAu+++lXffncXr\nr7/Co48+Rbt27bn//rto3jzK+16FhQUn3O4xOzuLn376gVdfnQHAbbeNYeDAwcyZM5vzzjufq666\nmg8+eIdNmzac8e9DSUkJU6e+wn//+ynz5n1FUFAQP/30A6+//g67du3kgw/e4cEHH2XmzHeZOPF5\nVqxYVtZDIW+88W/efvtDgoKCGDfuXu9zf97eUuEsIpXJUZLP/T/fzZyNnxIaEMqkXlNoH9qBpvWb\nElm/aa0J4eOpNeFslu3bt3HHHTcDpXtbP/LIE94tNDt1Kt0WMy1tFampK1m1KgWA4uJinE4nu3fv\npl270k+3iYldKS4u9r7v1q1baNmyFQEBgQQEBDJp0tRyX3ft2nR27MjkzjtLz+sWFhawZ88utm7d\nwsCBpXtlJyV1548/Fv6lZofD4a0ZICamLWPHHv/8cEJCEgDh4ZGsWZPOhg3r6dSpM1arlejoFjz4\n4KPHfF1m5naio1t6d9VKSurGhg3rAIiPTwRKN0dxOBzH/doiIqdqzb50xnx7HRkHNtE9sgfTz3+H\nqJBos8uqVLUmnAsef/qUPuVWlqPPOf+Z3e7n/e/IkaMZMuSCcs9brUcuhv/zlFSr1YZheI77de12\nP3r16sO4cQ+X+/WZM9/FUjbF5nivP9Y555KSg+Ueu1wu788P7yd9uE6bzYrHU/FUV4ulfF8ul5OA\ngIBjvqeIyJkyDIOP1n3Ag7/cR5G7iNsS7uSRno/X+Iu7TodupaoEnTp15rfffgYgN3c/r7/+bwCa\nNAln+/atGIbBypXLy72mou0eY2M7smLFcoqKijAMgxdfnExxcREtW57FunVrALyHkE9GcHAwubn7\nMQyDffty2LVrx3HXxsZ2ZPXqVFwuF/v37+Ohh0p31PpzYLdocRY7dmynsLAAgJUrVxAb2+mkaxIR\nOVkFzgLu+vE27llwOwH2QN698COe6POMTwYz1KJPzjXZoEGDWbFiKbfeOhq3283o0aWHlG++eSyP\nPDKepk2bec9TH1bRdo8vv/wGV111NbfffhNWq5V+/QYQEBDIlVdezaOPPsgvvywgJqbdSdfYsGFD\nunfvwY03jqRt23YnvNq6WbPmDB06jDvuuBnDMLjlltsBaN8+lptuGsltt93l7eH22+/mvvvuxGKx\nEh+fSEJCIsuWLT6l3z8RkRPZsH89Y769jvW560iK6Mob57/DWQ1amV1WldKuVGVq224qp8rX+wPf\n71H91W6+3h9Ufo8Hi/N4acULvLHqVYrcRdzY5RYm9H7atIu9qnNXKn1yFhGRGsXpdvLemreZvPRf\n7CvaR7P6zXnm3Oe4OOZvZpdWbRTOIiJSIxiGwTdbvuKpPx4j48Am6vsFk3zOY9wcP5YgvyCzy6tW\nCmcRETHd8r1LeXzhIyzevQibxcb1cWO4/+yHiAiKMLs0UyicRUTEFLlF+1m0ayGfb/yU/2XMAeCC\nVsN4tNeTtAs9+QmIvkjhLCIi1WJ/0T4W7VrIwp2/8vuu31i7Lx2D0muSE8OTeLz3M/SOOtfkKmsG\nhbOIiFSZFXuX8dmGj/l912+s2Zfm/fVAWyDnRvWjd9S59Gnelx7NemK1aPTGYQpnERGpdCv2LmPy\n0knM3/4dUBrGfaP6e8M4KbJbrZ9/XZUUziIiUmn+HMq9mvfh7q730Seqr8L4FCicRUTkjK3cu5yX\nvp/MVxu/AkpDedzZyfSJ6mtyZbWTwllERE5bWs5qJi1+iu+2zQOgZ7PejOuRTJ/mfbFYLCZXV3sp\nnEVE5LT8nLmA677+B0XuIs5p1ouJQ56mc/3uCuVKoHAWEZFT9lPmj4z8ejgGBm8N/YCL2lxCREQD\nn58fXl0UziIickoWbP+BUd9cjYHBuxd+xKCWg80uyeconEVE5KQt2P4DI78ZDqBgrkK641tERE6K\ngrn6KJxFRKRCP26f7w3m9y6cpWCuYgpnERE5oR+3f8+ob67GgoX3LpzFwJbnmV2Sz9M5ZxEROa7S\nYL6mNJiHzWJAi0Fml1QnKJxFROqwPQW72XZwGzsdmezI38FORya7HDu9Pz9QfIBAW6CCuZopnEVE\n6qBDrkOM/+WfzFo385jP1/cLJjo4mu6RPbgj6R5t5VjNFM4iInVMZv52bpg3glXZKcQ17sKgloOJ\nCokmOjiaqOAWRIdE08C/oSZ9mUjhLCJSh/ycuYBbvr+B/UX7GdFxFBP7Pk+gPdDssuRPFM4iInWA\nYRi8kjKNZ/54HJvFxuT+0xgZd4PZZclxKJxFRHycw+ngnh9vZ27G5zSr35wZQ9+je9MeZpclJ6Bw\nFhHxYZsPbGLUN9ewPncdPZv15s2h7xERFGF2WVIBDSEREfFBxe5iZq2byZBPB7A+dx03dbmVz/72\nhYK5ltAnZxERH7IjP5P30t/mg7XvknMom3r2evz7vDe4Mna42aXJKVA4i4jUcoZh8POOBbyVNp3v\ntn6Dx/DQKKARtyXcyeguN3FWg1ZmlyinSOEsIlJL5RUfYPa6D3k7/U0yDmwCID48kdGdb+Kytn8n\nyC/I5ArldCmcRURqkQNFuXy79Ru+2jyXBZk/UOwuxt/qz5XthzO6y010jeiu4SE+QOEsIlLD7Tu0\nj2+2fMmXm//HLzt+wuVxAdAhrCNXtP8H13QcSZN6TUyuUirTSYXzxIkTSU1NxWKxkJycTHx8vPe5\n+fPn89prr+Hv789FF13EiBEjWLx4MXfffTft2rUDoH379jz66KNV04GIiA9yOB18un42X2T8l4W7\nfsNtuIHSw9YXt/kbF7e5lLah7UyuUqpKheG8ZMkStm3bxuzZs8nIyCA5OZnZs2cD4PF4eOqpp/j8\n889p1KgRN910E4MHl27A3aNHD1566aWqrV5ExMccKMrlzdWvM33Va+QW5wLQLfJsLm5zKRe1uYRW\nDVubXKFUhwrDedGiRd7AjYmJIS8vD4fDQXBwMLm5uTRo0ICwsDAAevbsycKFC4mKiqraqkVEfExW\nYRavp/6bt9PexOHMJzQglHFnJ3NNx+toHqx/U+uaCsM5JyeHuLg47+OwsDCys7MJDg4mLCyMgoIC\ntm7dSlRUFIsXL6ZHjx5ERUWxadMmbr31VvLy8rjjjjvo06dPlTYiIlIb7czfwb9TpvHBmncpchcR\nERTJ/Wc/yMi4Gwj2Cza7PDHJKV8QZhiG9+cWi4VJkyaRnJxMSEgI0dHRALRq1Yo77riDCy+8kMzM\nTEaOHMl3332Hv7//cd83NDQIu912Gi1UnvDwEFO/flXz9f7A93tUf7Xb0f1t2r+JZ397lndT38Xp\ncdKyYUvG9xnP6KTRtXqXqLr0PaxKFYZzREQEOTk53sdZWVmEh4d7H/fo0YMPP/wQgClTphAVFUVk\nZCTDhg0DoGXLljRp0oS9e/fSokWL436d3NzC026iMoSHh5CdnW9qDVXJ1/sD3+9R/dVuh/tbv38d\nLy6fzOebPsVjeGjTMIa7u97HFe3/gZ/Nj/xcJ/k4zS73tNSV72Flvt/xVDhbu0+fPnz77bcApKen\nExERQXDwkUMtN954I/v27aOwsJAFCxbQq1cv5s6dy4wZMwDIzs5m3759REZGnmkfIiK11srdKxk9\n7zr6zTqHzzZ+TGxoR14f8ha/X72MqzuOwM/mZ3aJUoNU+Mm5a9euxMXFMXz4cCwWCxMmTGDOnDmE\nhIQwZMgQrrrqKkaPHo3FYuHmm28mLCyMQYMGcf/99/PDDz/gdDp5/PHHT3hIW0TEVy3bs4QXl0/m\nu23zAEgMT+Le7uMY2upCrBbtPSTHZjGOPolsIrMPhehwTO3n6z2qv5rHMAwKXYU4nA4cJQdxlDjI\nd+aTX5JPXvEBPt3wMb/sWABAnxZ9uDPhPga2OM9nJ3jVxu/hqajOw9qaECYicooWbP+Bcb/cS2b+\ndjyG54Rr+0UP5J/dHuBvCReQk+OopgqltlM4i4icJJfHxbNLnmHaiin4Wf3oFnk2If4hhPg1IMQ/\nhPr+wYT4hRDsH0KIfwhdmsSTGNEVwGc/LUvVUDiLiJyEXY6d3PL9aBbvXsRZDVox/fx3vMErUtkU\nziIiFZi/7Vvu+OEW9hft55KYy3hhwMs0CGhodlniwxTOIiLH4XQ7mbj4Sf6dMo0AWwDP9pvK9XFj\ndIhaqpzCWUTkGHbkZ3LzdzewbO8S2jSMYfrQd+nSJL7iF4pUAoWziAjgMTxszN3Air3LWL53GXMz\n5nCg+ACXt7uCyf2nEezv22MppWZROItInbS3cC8r9i4r/ZG1nJSsFeSXHPQ+X98vmCkDXmJEx1E6\njC3VTuEsInVKibuEsfNvYm7G5+V+vV2j9gxrfTFJkd3oFtGdTo07a6SmmEbhLCJ1Rom7hBu/G8W8\nLV+REJ7Eha0vomtkd5IiutIwoJHZ5Yl4KZxFpE5wup3c9N31zNvyFf2iB/L+sFnUs9czuyyRY9LU\ndRHxeU63k5u/v4FvtnxJ36j+vHfhRwpmqdEUziLi05xuJ7d8P5qvNs/l3Kh+vD9sNkF+QWaXJXJC\nCmcR8Vkuj4vb5t/Il5v/R+/m5yqYpdZQOIuIT3J5XIydfyNzMz6nZ7PezLzoE+r71Te7LJGTonAW\nEZ/j8ri4ff5N/HfTHM5p1osPL/5UwSy1isJZRHxKWs5qxnw7ks83fcbZTc/ho4s+Jdgv2OyyRE6J\nbqUSkVrvYHEeczZ+ysy175GavRKAs5uew6yLP9PYTamVFM4iUisZhsHi3YuYufY95mZ8ziHXIWwW\nG0NbXci1HUcx+KzzsVv1T5zUTvqTKyK1SrG7mBmr3+D9NW+TcWATAK0atObajiP5R4draFq/mckV\nipw5hbOI1BpZhVncMO9alu5ZTIAtgL+3u4oRnUbRq3kfrBZdQiO+Q+EsIrVCWs5qRn49nB2OTC5v\ndwWT+k6hUWCo2WWJVAmFs4jUeF9t/oLb599EoauQ5HMe4+6u92kbR/FpCmcRqbEMw+CF5c8zacnT\nBNnr884FHzKszcVmlyVS5RTOIlIjHXId4p4fx/L5ps+IDm7Be8Nm0blJF7PLEqkWCmcRqXF2O3Yx\n6purScleyTnNevHW0A8IDwo3uyyRaqNwFpFqk1WYxRMLHyEtZxUBtgAC7fXK/htIw/oh4LIRYAvk\nu63fsLdwD1d3GMFz/V8gwBZgduki1UrhLCJVzjAMPtv4MQ//Oo7c4lzq+wXjMdwUuYowMP6y3mqx\n8mSfidwSf7su/JI6SeEsIlVqb8EeHvj5HuZt/ZogexD/6vs8N3S+CavFimEYOD1OilyHCG7kx86s\nHIpdxYQENCAyKNLs0kVMo3AWkSphGAYfr/+IR35/kLziA/Rp3pcXBr5Cq4atvWssFgv+Nn/8bf6E\nB4dgPaS9lkVA4SwiVWC3Yxf3/XQX87d/R32/YJ7tN5VRcaM1xUvkJCmcRaTSGIbBrHUzefT3hzhY\nkke/6IFMHfASLRucZXZpIrWKwllEKkVu0X7++dNdfLV5LsF+IUwZ8BIjOo7SBV0ip0HhLCJn7I9d\nC7lt/o3sdOygZ7PevDp4OtEhLcwuS6TWUjiLyGlzeVxMXfYcU5c/B8C4s5O5t9sD2Kw2kysTqd0U\nziJyWnbkZ3Lb/BtZvHsR0cEteHXIm/Rs1svsskR8gsJZRE7ZFxn/5Z8/3UVe8QH+FvN/TO7/orZv\nFKlECmcROSmGYbD14BZeWfki7695h3r2ekwd8DLXdhypi75EKpnCWUSOa0/Bbn7d8TO/7fyFX3f8\nzA5HJgBxjbvw+pC3aB8Wa3KFIr5J4SwiXo6SfH7KXMBvO3/m1x0/s/HABu9zoQGhXNzmUvpFD2B4\nh2sJtAeaWKmIb1M4i9RxhmGwdM8SZq59l/9tmkOhqxCAIHt9zms5hHOj+tMvuj9xTbpowpdINVE4\ni9RROYdy+GT9LGaufZcNuesBaNmgFVe2/wcDWpxHUkRX/G3+JlcpUjcpnEXqELfHzc87FjBz7XvM\n2/IVTo8Tf6s//9f271zbaRTnRvXTp2ORGkDhLFJH/L7zV+7/+W4yDmwCoGNYJ0Z0GsXf219FWGBj\nk6sTkaMpnEV83MHiPJ5cNIH31ryF1WLlmg7XMTLuBpIiuukWKJEa6qTCeeLEiaSmpmKxWEhOTiY+\nPt773Pz583nttdfw9/fnoosuYsSIERW+RkSqx/db53H/z/ewu2AXHcM68cLAV+ga2d3sskSkAhWG\n85IlS9i2bRuzZ88mIyOD5ORkZs+eDYDH4+Gpp57i888/p1GjRtx0000MHjyY7du3H/c1IlL1cg7l\n8Mhv45mz8RP8rH6MOzuZu7r+Uxd4idQSFYbzokWLGDx4MAAxMTHk5eXhcDgIDg4mNzeXBg0aEBYW\nBkDPnj1ZuHAhmZmZx32NiFQdwzD476bPSP71AfYV7aNrRDdeGPhvOjbuZHZpInIKKrwsMycnh9DQ\nIzNzw8LCyM7O9v68oKCArVu34nQ6Wbx4MTk5OSd8jYhUPsMwWLJ7Mdd9/Q9u+X40ha5Cnuwzka8u\nn69gFqmFTvmCMMMwvD+3WCxMmjSJ5ORkQkJCiI6OrvA1xxMaGoTdbu42c+HhIaZ+/arm6/2B7/f4\n5/6yCrJ4P/V93lz5Juty1gEwsNVApl8ynZiwGDNKPCN17fvni3y9x+rqr8JwjoiIICcnx/s4KyuL\n8PBw7+MePXrw4YcfAjBlyhSioqIoLi4+4WuOJTe38JSLr0zh4SFkZ+ebWkNV8vX+wPd7PNxf6b3K\nP/LBmvf4duvX5e5VvqbjSPpFD8DittS634u68v3zZb7eY2X3d6Kgr/Cwdp8+ffj2228BSE9PJyIi\noty54xtvvJF9+/ZRWFjIggUL6NWrV4WvEZFTt/XAVp5d8gzdP+jC8C//zpeb/0fbRu155txnWXX9\nel4//236txio26NEfECFn5y7du1KXFwcw4cPx2KxMGHCBObMmUNISAhDhgzhqquuYvTo0VgsFm6+\n+WbCwsIICwv7y2tE5NQdch3i681f8OG6D/h1x08ABPuFcF2nGxjRcSSJEV0VxiI+yGKczAnhamD2\noRAdjqn9fKVHwzBYlZ3CzLXvMWfjpxwsyQOgb8u+XBFzNX9r+3/U96tvcpWVz1e+f8fj6/2B7/dY\nnYe1NSFMpIbILdrPJ+tn8eG6D1izLw2AyKCm3ND5RoZ3uIae7br69D98InKEwlnEZFmFWbya8hLv\npM2g0FWAn9WPi9tcyjUdRzCgxXnYrfprKlLX6G+9iEl2O3bx75RpvJf+NkXuIprVb864HslcFXs1\nTeo1Mbs8ETGRwlmkmu3Iz+SlFVP5cO37lHhKiA5uwV1d/8nVHUcQYAswuzwRqQEUziLVZGveFl5a\nMZXZ6z/E6XFyVoNW3NP1fq6MHa6Z1yJSjsJZpIrtO7SPKcsm8U76DFweFzGN2nJvtwe4vN2VOp8s\nIsekfxlEqkiRq4jpq//Di8snk19ykNYN2zC+x8NcGnM5Nqu5o2pFpGZTOItUMo/h4fONn/LMH0+w\nw5FJaEAoz5z7LKPixujwtYgj8BkqAAAgAElEQVScFIWzSCVauPM3Hl/4MCnZK/G3+nN74t3c0+0+\nGgY0Mrs0EalFFM4ilWBHfibJvz7AvK1fA3B5uytIPmcCLRucZXJlIlIbKZxFztC8LV9z14+3cqD4\nAD2b9ebx3k/TNbK72WWJSC2mcBY5TSXuEp76YwKvp/6bQFsgz/d/kZGdbtBGFCJyxhTOIqdha94W\nbvn+BlZmraBdo/a8cf47xDXpbHZZIuIjFM4ip+iLjP9yz4I7yC85yFWxVzOp3xSC/bRfuYhUHoWz\nyEkqchUxYWEyb6e9SZA9iJcGvcbwDteaXZaI+CCFs0gFDMNgZdZy7v/5HtJyVtExLI7p579D+7BY\ns0sTER+lcBY5jowDG/lswyfM2fgJm/MyALiu0w08fe4k6tnrmVydiPgyhbPIUXY7dvHfTXOYs/ET\nUrNXAlDPXo//a/t3ru54HQNaDDK5QhGpCxTOUuc53U4+2/gxH6//iN93/oqBgc1iY3DL87m8/ZVc\n0PoiXfAlItVK4Sx1Vom7hI/Xf8SLyyezPX8bAOc068Xl7a7kkpjLaFKvickVikhdpXCWOqfEXcKs\ndTOZtmIKmfnbCbAFMKbLzdyWcKfGbYpIjaBwljqj2F3MR2s/4KUVU9nhyCTQFshNXW7lzq730rR+\nM7PLExHxUjiLzzIMg9zi/Ww+kMGKvct4LfUVdjp2EGgL5Jb4sdyRdA+R9ZuaXaaIyF8onKXWc3vc\nrMpOIWv3DlIy09iSt5kteRlszttMXvEB77p69nrcmnAHtyfdTWRQpIkVi4icmMJZarU9Bbu55fvR\nLNr1e7lf97f606pha3o260XrhjHENGrLha0vJiIowqRKRUROnsJZaq2fMxdw2/wx5BzKYchZQ/m/\nuEtpYmtOm4YxRAVHY7PazC5RROS0KJyl1nF73ExZ9ixTlj2L3WrnmXOf5cYutxIR0YDs7HyzyxMR\nOWMKZ6lVsgqzuG3+jfy64ydahLRk+vnv0DWyu9lliYhUKoWz1BoLd/7GLd+PZm/hHoa2upCXBr1G\naGCY2WWJiFQ6hbPUeB7Dw8srXuBfS57CgoUJvZ5mbOKdWCwWs0sTEakSCmep0dJz0nj09wf5becv\nNKvfnDfOf4dzmvU0uywRkSqlcJYaaW/hXp5d/DQfrnsfj+Hh/LMu4MVBr2retYjUCQpnqVEOuQ7x\neuq/mbZiKgVOB7GhHXiizzMMajnE7NJERKqNwllqBMMw+HzTpzy96HF2ODJpHNiYx3o9yXWdrsdu\n1R9TEalb9K+emG7ZniU8+vuDLN+7DH+rP3ck3cM9Xe+jQUBDs0sTETGFwllMNXfT59z8/Q14DA+X\nxlzOI70e56wGrcwuS0TEVApnMc28LV9z6/wxBNnr8+6FH9I3ur/ZJYmI1AgKZzHFj9vnc+O3I/G3\n+vPhxZ/Ss1kvs0sSEakxrGYXIHXP7zt/5fpvrsFqsfL+sNkKZhGRP9EnZ6lWS3Yv5tqvrsJtuHl/\n2CwdyhYROQaFs1SblKwVXP3V3yl2FzFj6Pu6d1lE5DgUzlIt0nJWc9UXl1HgdPCfwTMY1uZis0sS\nEamxFM5S5dbvX8dVX1xKXnEeLw16jcva/d3skkREajSFs5y2Qmchzy2dyPdb52Gz2vCz+uNnteNn\n88ff6o/dasff5s/yvcvIOZTD5P7T+EeHa8wuW0SkxlM4y2n5Y9dC7l4wli15mwn2C8Hf5keJ24nT\nU0KJuwQDw7vWbrUz8dznGBl3g4kVi4jUHicVzhMnTiQ1NRWLxUJycjLx8fHe52bOnMncuXOxWq10\n7tyZhx9+mDlz5jBt2jRatmwJQO/evbntttuqpgOpVgXOAv61+Emmr/oPALcl3MmD5zxCPXu9cuvc\nHjclnhJcHidWi436fvXNKFdEpFaqMJyXLFnCtm3bmD17NhkZGSQnJzN79mwAHA4HM2bM4LvvvsNu\ntzN69GhSUlIAGDZsGOPHj6/a6qVaLdr1O3f/OJatB7fQtlE7pg16lbObnnPMtTarjXrWekC9Yz4v\nIiLHV2E4L1q0iMGDBwMQExNDXl4eDoeD4OBg/Pz88PPzo7CwkKCgIA4dOkTDhtqswNc4nA6e+eNx\nZqx+A6vFyh1J9/DA2Q/95dOyiIhUjgonhOXk5BAaGup9HBYWRnZ2NgABAQHcfvvtDB48mIEDB5KQ\nkEDr1q2B0k/cY8aMYdSoUaxZs6aKypeq5HA6+HrzlwyY3ZsZq9+gfWgsX13+PY/1elLBLCJShU75\ngjDDOHKhj8Ph4PXXX2fevHkEBwczatQo1q1bR0JCAmFhYQwYMICVK1cyfvx4vvjiixO+b2hoEHa7\n7dQ7qETh4SGmfv2qVlF/hc5CFmYuZMGWBSzYuoClu5bi8riwWqw8dO5DPNb/MQLtgdVU7emp69/D\n2k791X6+3mN19VdhOEdERJCTk+N9nJWVRXh4OAAZGRm0aNGCsLAwALp3705aWhpXXHEFMTExACQl\nJbF//37cbjc22/HDNze38IwaOVPh4SFkZ+ebWkNVOlZ/hmGweM8f/JT5A7/v/JUVe5fh9DgBsFls\nJEYk0bt5Xy5r93e6NIknP9dJPk4zyj8pdfF76EvUX+3n6z1Wdn8nCvoKw7lPnz68/PLLDB8+nPT0\ndCIiIggODgYgKiqKjIwMioqKCAwMJC0tjf79+zN9+nSaNWvGxRdfzIYNGwgLCzthMEv12+3Yxfhf\n/sm8rV8DYLVYiW+SQJ+ofpwb1ZcezXoS4t/A5CpFROqmCsO5a9euxMXFMXz4cCwWCxMmTGDOnDmE\nhIQwZMgQxowZw8iRI7HZbCQlJdG9e3eio6N54IEHmDVrFi6Xi2eeeaY6epGT4DE8vL/mHZ5c9Bj5\nJQfp07wvtyXeQc9mvWkQoIv5RERqAotx9ElkE5l9KKQuHI75Y+MK/vnTXSza9TsN/BvyeO+nubbj\nSCwWi9nlVYq68D1Uf7WXr/cHvt9jjTqsLbWf0+3kX7/+iyd+foJidzHDWl/CpH6TaVq/mdmliYjI\nMSicfVxq1kru/elO0nJWEREUyb/6TuaSmEvNLktERE5A4eyj9hftY/LSSbyVNh2P4WFM0hjGJz1G\no8DQil8sIiKmUjj7mBJ3CTNWv8HU5c+RV3yANg1jeL7/i1yedLFPnwsSEfElCmcfYRgGX23+gicX\nPcrWg1toFNCIp/tM4vrON+Jv8ze7PBEROQUKZx+QmrWSxxYms2jX79itdm6Ov437uo8nNDDM7NJE\nROQ0KJxrsV2OnUxc/CQfr/8IgAtaDWNC76eIadTO5MpERORMKJxroW0Ht/LyiheZte4DSjwlxDXu\nwpN9JtI3ur/ZpYmISCVQONciG3M3MG3FFD7b8DFuw03rhm24t9sDXNl+ODarxqOKiPgKhXMtkJ6T\nxovLJzM343MMDDqEdeTurvdxadvLsVv1LRQR8TX6l72GMgyDpXuW8MrKF7ybU8SHJ3Jvtwe4sPVF\nWC0VbsUtIiK1lMK5BjEMgxVZy5i76b98ufl/ZOZvB+Dspufwz24PMKjlEJ+Zgy0iIsencDaZx/Cw\nfO9S5mb8ly8z/sdOxw4Agv1C+Hu7q7i200j6NO+rUBYRqUMUzibZfnAb01e9xhcZ/2NXwU4AGvg3\n5KrYq7kk5jIGtBhEgC3A5CpFRMQMCudqtrdgDy8sf57317yD0+OkYUAjhne4lr/FXEbf6AEKZBER\nUThXl9yi/byychpvrv4Ph1yHaNWgNeN6JPO3mP/TeE0RESlH4VzFHE4Hb6S+yr9TXiK/5CDN6jfn\nqT6TuLrDCPxsfmaXJyIiNZDCuYrklxzko7Uf8OKKyeQcyiEsMIwnek/k+s5jqGevZ3Z5IiJSgymc\nK4Hb42ZD7nqW713q/bF+/zoMDIL9Qhh3djK3JIwlxL+B2aWKiEgtoHA+DXsL9rAyawUr9i5j+d6l\nrMhaToHT4X0+yF6f3s3PpXfUuYzpcjNhgY1NrFZERGobhXMFDhTlkpK9kpSsFazMWkFK1gp2F+wq\nt6Z9aCzdIs/2/ogN66CxmiIictqUIMeQmb+dyUsn8cfuhWzJ21zuuYigSC5oNYzEiK4kRXSja2Q3\nGgY0MqlSERHxRQrno7g9bt5Ke4Nn/niSQlcBDQMa0S96IEkRXcvCuCvN6jfXtC4REalSCucy6Vnp\njPr8BpbvXUpoQCjP9pvClbHDtcGEiEgdZsnKwm91Cra01XD+IOiYVC1ft86Hc7G7mGnLpzBtxRSc\nHieXtb2cp899joigCLNLExGR6mIYWPfsxr4qFXvqSuyrU7GvSsW2+6hrjFavhDc/qJZy6nQ4L92z\nmH8uuJP1ueuIColiUt+pDG11odlliYhIVTIMrDsyS4N41Ursq1LxW5WKNTur3DJ302YUD70QV5cE\nXAlJNLxsGBwyqqXEOhnOewv3Mm35ZGasfgMDg+vjxjDtkqkUH9S5ZBERn2IYWLduwW9VSlkYp2Bf\nnYp1//5yy9zRLSgedgmu+ARcCYk4OydgREaWf6/gYDiUXy1l15lw3ndoH19u/h//2zSHhbt+w2N4\naNuoHVMHvkLPZr1oEBBCNtXzmy4iIlXA48G2OaP0sLQ3iFdhPZhXbpm7VWuKzu1fGsTxibi6JGA0\nrlnzKHw6nA8U5fL1li/576bP+HXHz7gNNwDdI3twebsrGNHpegLtgSZXKSIip8zlwrZpY2kAH/5U\nvHoV1oIjA6EMiwV3TFtKBg/B1SURV0Iirs5dMBqFmlj4yfHJcF6xdxlTlj3LT5k/4vQ4AUgMT+LS\ntn/n0rb/R3RIC5MrFBGRk+Z0Ylu/ruzQdFkQp6/GcuiQd4lhteJuH0tJl9LD0q74siAODjGx8NPn\nk+H8xqrX+H7bt8Q17sJlbS/nb23/j9YN25hdloiIVKS4GPu6NdhTU45csLV2DZbiYu8Sw27HHdsR\n5+HD0vEJuDp1hvr1TSy8cvlkOE/u/yIP95xAi5CWZpciIiLHc+gQ9vTVZYekU0sDed0aLC6Xd4nh\n54erY1zpp+HDn4o7xkGgb5+S9MlwDvYPIdi/dh7KEBHxSQ4H9vQ0/FYduVjLtmE9Frfbu8QIDDwS\nwvFl54hjO4K/v4mFm8Mnw1lERMxjOZiHPW116fnh1NJbl2wbN2AxjtwjbATVx9Xt7KMOTSfibh8L\ndsUSKJxFROQMWHL3Y1+9CntqCmxIJ3TJUuxbym8Y5AkOwdmrz5Hzw/GJuGPags1mUtU1n8JZRERO\niiUnB/uqlHIDPWzbt5VbY23UiJK+A8qumE7AFZ+Au1UbsGqfglOhcBYRkb+w7t1z5Lalw4emd+4o\nt8bTuDElA8/DFZ+IMz6RhgP7sK9+Y9DOfWdM4SwiUpcZBtZdO/+64cPePeWWuSObUjxkqHfOtCs+\nAU/zqPJBHB4C2Zq0WBkUziIidYVhYN2+rWyjh5Qjc6Zzcsotc0dFU3zBRd7D0q6EJDyRTU0qum5S\nOIuI+CKPB9vWzUcN80jFvjoF64ED5Za5W55F8cV9cB6+halLAkZ4uElFy2EKZxGR2s7txpaxqdyt\nS/bVq7DmHyy3zNUmhpIBg3DFlx6WdnWJxwgNM6loORGFs4hIbeJyYduw3ntI2i81BXvaaiyFBd4l\nhsWCu117Ss6/4Mgwj85dMBo0NLFwORUKZxGRmqqkBPv6teUv1kpPw1JU5F1i2Gy423fAFZ9Qdmg6\nEVdc59K9h6XWUjiLiNQERUXY16YfOSy9KhX72nQsJSXeJYafH64OnY7sQ3x4w4d69UwsXKqCwllE\npLoVFGBPT8O+uvRiLb/UFGzr15afMx0QgCuu85Hzw/EJuDp0goAAEwuX6qJwFhGpQhZHPva01ZCx\nlpCFi0unam3cgMXj8a4x6tXDldSt7NB0Eq4uCbhjO4Cfn4mVi5lOKpwnTpxIamoqFouF5ORk4uPj\nvc/NnDmTuXPnYrVa6dy5Mw8//DBOp5MHH3yQXbt2YbPZ+Ne//kWLFi2qrAkRkZrAknegdM704X2I\nV6Viy9jk3fAhEPDUD8bZo2fZ1dKl9xC727bThg9SToV/GpYsWcK2bduYPXs2GRkZJCcnM3v2bAAc\nDgczZszgu+++w263M3r0aFJSUtiyZQsNGjRgypQp/Pbbb0yZMoUXX3yxypsREakulv37vPOlDw/1\nsG3dUm6Np0FDnH364uqSQFDfXuxvFYu7TYzmTEuFKgznRYsWMXjwYABiYmLIy8vD4XAQHByMn58f\nfn5+FBYWEhQUxKFDh2jYsCGLFi3isssuA6B3794kJydXbRciIlXIkpV11D7EZRs+7Mgst8YTGkpJ\n/4Glc6bLBnp4WrX2jrcMCg/BrdGWcpIqDOecnBzi4uK8j8PCwsjOziY4OJiAgABuv/12Bg8eTEBA\nABdddBGtW7cmJyeHsLDSG9utVisWi4WSkhL8T7BhdmhoEHa7uduHhYeHmPr1q5qv9we+36P6q2KG\nAbt2wfLlsGLFkf/u2lV+XUQEXHABdOsGXbtCt25YW7bE32Lh+P/K1YD+qoGv91hd/Z3ySQ7jqM2y\nHQ4Hr7/+OvPmzSM4OJhRo0axbt26E77meHJzC0+1lEoVHh5Ctg//X62v9we+36P6q2SGgXVHZrnz\nw36pKVhzssstczdrjmvoheU3fGja7K87L+U4TvjlfP37B77fY2X3d6KgrzCcIyIiyDlqKHpWVhbh\nZXNXMzIyaNGihfdTcvfu3UlLSyMiIoLs7Gw6dOiA0+nEMIwTfmoWEalShoF165YjE7UOb/iwf3+5\nZe4WLSkedon31iVnfBJGRIRJRUtdVmE49+nTh5dffpnhw4eTnp5OREQEwWWTZ6KiosjIyKCoqIjA\nwEDS0tLo378/AQEBzJs3j759+7JgwQLOOeecKm9ERAQo3fBhc0bpRK1Vqd6BHtaDeeWWuc9qRdG5\n/Y8M8+iSgNG4sUlFi5RXYTh37dqVuLg4hg8fjsViYcKECcyZM4eQkBCGDBnCmDFjGDlyJDabjaSk\nJLp3747b7WbhwoVcffXV+Pv7M2nSpOroRUTqGpcL28YN5eZM29JWYy04cojZsFhwx7SlZPCQ8hs+\nNGxkYuEiJ2YxTuaEcDUw+zyFzpXUfr7eY53vz+nEtm4tfqtTj+y+tCYNy6FD3iWG1Yq7fWzp+eGy\nfYhdnbtgBJt/kZKvf//A93usUeecRUSqXXEx9nVrjtqLeCX2NX+aM223447tiPPwaMv4xNI50/Xr\nm1i4SOVQOIuIuQ4dwr4mDTavI3jh4tIwXrcGi9PpXWL4++PqGHckhLvElwZxYKCJhYtUHYWziFQf\nhwN7elq5gR62Deu8Gz7UA4zAwNLwjU/03rrkiu0IuuND6hCFs4hUCcvBvKPmTJfevmTbtNE7ZxrA\nCArC1e1snPEJBJ1bNt6yfazmTEudp78BInLGLLn7y422tK9Kwb5lc7k1nuAQnL36lLtYyx3TFmyl\nkwE13lLkCIWziJwSS04O9lUp+K1KOTJnevu2cms8jRpR0ndAWQiX3kfsbtVGGz6InCSFs4gcl3Xv\nniPDPA4H8a6d5dZ4GjemZOB53n2IXfEJeFqe9dfxliJy0hTOIlI63nLXzrJbl1K82yDasvaWW+aO\nbErxkKFlU7UScSUk4mnWXEEsUskUziJ1jWFg3ba1dKLWqtTST8arU7Hu21dumTsqmuILLvIelnbF\nJ+KJbGpS0SJ1i8JZxJd5PNi2ZPzpYq1UrHkHyi1zt2xFca9zyzZ7SMDVJRGjbIMbEal+CmcRX+F2\nY8vYdNQ54hTsq1dhdZS/AtrVug0lAwfh6lJ6WNrVJR4jNMykokXkWBTOIrWRy4Vtw3rv+WG/VanY\n01ZjKSzwLjEsFtzt2lMSn1huspYR0sDEwkXkZCicRWq6khLs69eWjrf8/Y/SQF6TjqWoyLvEsNlw\nt+9Qelg6IbH0U3FcZyjb3lVEaheFs0hNUlSEfW166VXTq1NL/7s23Ttnuh5g+Pnh6tDpyKfh+ITS\nOdP16plbu4hUGoWziFkKC7Gnr/aeH/ZblYpt/VosLpd3iREQgKtzF1xdEql3bk9yW7XH1TEOAgJM\nLFxEqprCWaQaWBz52NNWH7lYa3Uqtg3rsXg83jVGvXqlGz0kJHoHerhjO4CfHwD1wkNwabylSJ2g\ncBapZJa8A0duXVqdgj01BdvmjHIbPnjqB+Ps0bPsaunSw9Pudu29c6ZFpG5TOIucAcu+fWW3LKXi\nVzZdy7Zta7k1ngYNcfbpWxrCCaW3L7lbx2jOtIgcl8JZ5CRZsrLwK/sk7J0zvSOz3BpPaCgl/Qfi\nik8su2o6AU+r1hpvKSKnROEs8meGgXXP7tIALhttaV+Vim33rnLLPE3CKT5vSNmh6dKrpj3RLRTE\nInLGFM5StxkG1h2ZZbcupZQdmk7FmpNdbpm7WXOKh15YfsOHyKYKYhGpEgpnqTsMA+uWzfiVfRI+\nHMjW3Nxyy9wtWlJ80d/K7iNOwNklESMiwqSiRaQuUjiLb/J4sG3O+Ouc6YN55Za5W7WmqO+AI8M8\n4hMwwhqbVLSISCmFs9R+Lhe2TRth3nrq/7ao7BamVVgLHN4lhsWCO6YtJYOH4IpPKg3iLvEYDRuZ\nWLiIyLEpnKV2cTqxrV+HX9mGD/ZVqdjTV2M5dAiAIMCwWnG3jy2/4UPnLhjBIebWLiJykhTOUnMV\nF2Nft+aoW5dWYl+7BktxsXeJYbfjju2IMz6Ben16kts6FldcFwgKMrFwEZEzo3CWmuHQoXJzpu2r\nUrGvW1N+zrS/P66OceU3fOgYB4GBgMZbiojvUDhL9XM4sKetPjLQ4/Ccabfbu8QIDCw32tIVn4Cr\nQyfw9zexcBGR6qFwliplOZhXtuHD4XPEKdg2bSw3Z9oICsLV7Wyc3k/Eibjbx4JdfzxFpG7Sv35S\naSy5+/+y4YN9y+ZyazwhDXD26nPUrUuJuGPaasMHEZGjKJzltFhycrCvWonf4TBelYJt+7ZyazyN\nGlHSd0BpCCck4oxPLJ0zrQ0fREROSOEsFSqdM51S7mIt266d5dZ4GjemZOB53n2IXQmJeFq01HhL\nEZHToHCWIwwD684dR4VwWRBn7S23zB3ZlOIhQ8tCuHSgh6d5lIJYRKSSKJzrKsPAun0b9lUppYem\ny3Zfsu7bV26ZOyqa4gsuKr1yuuwcsSeyqUlFi4jUDQrnusDjgY0bCVjwW7kLtqwHDpRb5m7ZiuLe\nfUuvmi67hclo0sSkokVE6i6Fs69xu7Ft2lj+HPHqVeDIp8FRy1xtYigZeB6uzgneT8VGo1DTyhYR\nkSMUzrWZy4Vt/Trsq1PxO7z7UvpqLIWF3iWGxYK7XXusZ3fHERtXegtTl3iMkAYneGMRETGTwrm2\nKCkpnTN91D7E9jXpWIqKvEsMmw13+w6lexAnJOLqkogrrjMEBxMeHsIhjbYUEakVFM41UVER9rXp\n3tGW9tQU7GvTsTid3iWGnx+uDp3Kz5nu1Bnq1TOxcBERqQwKZ7MVFGBPTyv9JLwqFb/UFGzr15af\nMx0QgKtzlyP7ECck4ortCAEBJhYuIiJVReFcjSyOfOyrV5VepHV4w4eNG7B4PN41Rr16uJK6eSdq\needM+/mZWLmIiFQnhXMVseQdKA3iw+eHU1Owbc4ot+GDp34wzh49jzo0nYi7XXvNmRYRqeMUzpXA\nsn9fudGWfqtSsG3dUm6Np0FDnH36lt/woU2M5kyLiMhfKJxPkSUr68g+xIc3fNiRWW6NJzSUkv4D\nccUnll01nVC64YPGW4qIyElQOB+PYZRu+HB4H+Kyq6Zte3aXW+ZpEk7xeUPKPg2XzZmObqEgFhGR\n03ZS4Txx4kRSU1OxWCwkJycTHx8PwN69e7n//vu96zIzM7nvvvtwOp1MmzaNli1bAtC7d29uu+22\nKii/khgGbNuG/4+/HblqelUq1uyscsvcTZtRPPTC8hs+NG2mIBYRkUpVYTgvWbKEbdu2MXv2bDIy\nMkhOTmb27NkAREZG8v777wPgcrm47rrrGDRoEN9++y3Dhg1j/PjxVVv96TAMrFu34Hd4vGXZBVvk\n5tLwqGXuFi0pvvDi0tuWEhJxdk7AiIw0rWwREak7KgznRYsWMXjwYABiYmLIy8vD4XAQHBxcbt3n\nn3/O0KFDqV+/ftVUejo8HmybM0p3XDpqzrT1YF65Ze5WrWHw4KPGWyZgNG5sUtEiIlLXVRjOOTk5\nxMXFeR+HhYWRnZ39l3D+5JNPeOutt7yPlyxZwpgxY3C5XIwfP55OnTpVYtkn5v/tNwS98iK2tNVY\nCxzeXzcsFtwxbSkZPKR0tGVC2Zzpho003lJERGqMU74gzDjqPt3DVq5cSZs2bbyBnZCQQFhYGAMG\nDGDlypWMHz+eL7744oTvGxoahN1eSff3/vYjLF0MHTtC166lP7p1w5KYiD0k5LhNh4eHVM7Xr6F8\nvT/w/R7VX+3m6/2B7/dYXf1VGM4RERHk5OR4H2dlZREeHl5uzU8//USvXr28j2NiYoiJiQEgKSmJ\n/fv343a7sZ1guEZubuFxnztlTz4Hjzz91/GWRUDRsT8dh4eHkO3Dn5x9vT/w/R7VX+3m6/2B7/dY\n2f2dKOgrnIDRp08fvv32WwDS09OJiIj4yyHt1atX06FDB+/j6dOn8+WXXwKwYcMGwsLCThjMlc5i\n0dxpERGptSr85Ny1a1fi4uIYPnw4FouFCRMmMGfOHEJCQhgyZAgA2dnZND7qAqpLLrmEBx54gFmz\nZuFyuXjmmWeqrgMREREfYzGOdRLZBGYfCtHhmNrP13tUf7Wbr/cHvt9jjTqsLSIiItVL4SwiIlLD\nKJxFRERqGIWziIhIDaNwFhERqWEUziIiIjWMwllERKSGUTiLiIjUMApnERGRGqbGTAgTERGRUvrk\nLCIiUsMonEVERGoYhbOIiEgNo3AWERGpYRTOIiIiNYzCWUREpIaxm11AVZo4cSKpqalYLBaSk5OJ\nj4/3Pjdz5kzmzp2L1baYIkUAAAjjSURBVGqlc+fOPPzww7hcLh5++GG2b9+O2+1m3LhxdO/eneuu\nu47CwkKCgoIAGD9+PJ07dzarLa9T7W/OnDlMmzaNli1bAtC7d29uu+021q1bx+OPPw5AbGwsTzzx\nhBnt/MWp9vfaa6+xcOFCADweDzk5OXz77bcMGjSIpk2bYrPZAJg8eTKRkZGm9PRnJ+px/vz5vPba\na/j7+3PRRRcxYsSI475m9+7djBs3DrfbTXh4OM8//zz+/v5mteV1Ov0999xzLF++HJfLxS233ML5\n55/Pgw8+SHp6Oo0aNQJgzJgxDBgwwIyWyjnV/hYvXszdd99Nu3btAGjfvj2PPvqoz3z/PvnkE+bO\nnetdk5aWxsqVK2vsv6EAGzZsYOzYsVx//fXeP4OHLVy4kKlTp2Kz2ejXrx+33347UE1/Bw0ftXjx\nYuPmm282DMMwNm3aZFx11VXe5/Lz842B/9/enYVE+f1xHH+PS6Y5mmMpLoXpRcuNCBWZqWkZFdFC\nV5LYoheRGhSVFaXdhFoWLRaaFkRZRioRJSlRQdRkClKomClEk+Ve6ailTud3IT5objl//uM4nNfd\n88h5eD5+Pec8c56jhoWJvr4+IYQQu3fvFhUVFSI/P18kJycLIYSora0V27dvF0IIERUVJT58+GDa\nABMwJl9BQYFITU0dca2oqCjx7t07IYQQBw8eFC9evDBBgvEZk2+owsJCkZ2dLYQQIiwsTOj1ehPd\n+b8bL6PBYBAhISGira1NGAwGsWfPHvHt27cx2xw9elQUFRUJIYQ4d+6cyM3NNXGakYzJp9VqRWxs\nrBBCiPb2dhEaGiqEECIxMVE8e/bM5BnGY0y+N2/eiISEhBHXspT6/d3+1KlTQgjzHEOFEKKrq0tE\nRUWJEydOiFu3bo34+oYNG8TXr1+FwWAQkZGR4uPHjybrgxa7rK3Valm7di0Afn5+/Pz5E71eD4Ct\nrS22trZ0d3fT399PT08Pzs7ObN68mWPHjgGg0Wj48ePHlN3/RIzJN5re3l4aGhqUJ+KwsDC0Wq1p\nQozjf8nX39/P3bt3RzwFm5vxMn7//h0nJyc0Gg1WVlasWLGC169fj9mmtLSUNWvWANOjhmPlW7Zs\nGRcvXgTAycmJnp4eDAbDlGUYjzH5xmIp9RvqypUr7Nu3z+T3PRkzZswgOzsbNze3EV/T6XQ4Ozvj\n4eGBlZUVoaGhaLVak/VBi52cW1tbcXFxUY41Gg0tLS0A2NnZERcXx9q1awkLC8Pf358FCxZga2uL\nnZ0dADdv3mTTpk1K+0uXLrFjxw6SkpL49euXacOMwph8AG/fviUmJoadO3dSXV2tdLJBrq6uynWm\nkrH5AEpKSli1ahUzZ85UziUnJxMZGUl6ejrCTP4o3ngZNRoNXV1dfPr0ib6+PkpLS2ltbR2zTU9P\nj7KENh1qOFY+a2trZekzPz+fkJAQ5XXE7du3iY6O5sCBA7S3t5s+0F+MyQdQV1fH3r17iYyM5NWr\nVwAWU79B79+/x8PDg7lz5yrnzG0MBbCxsRk2TgzV0tKCRqNRjgfzm6oPWvQ756GGDsh6vZ6srCye\nPHmCo6MjO3fupKamhkWLFgED7zOrqqrIzMwEIDo6moULFzJ//nySk5PJzc0lJiZmSnKM5V/y+fv7\no9FoWL16NRUVFSQmJpKTkzPmdczJZOpXUFAw7L35/v37CQ4OxtnZmbi4OIqLi1m/fr3JM0xkaEaV\nSkVqairHjx9HrVbj7e09YZvxzpmDyeR7+vQp+fn53LhxA4AtW7Ywe/ZsFi9ezLVr18jIyCApKcmk\n9z+Rf8nn4+NDfHw8GzZsQKfTER0dTUlJyZjXMSeTqV9+fj7btm1TjqfDGGqs/1cftNhPzm5ubsOe\n5Jqbm5WnuPr6eubNm4dGo2HGjBksXbqUyspKAO7fv8+zZ8+4evUqtra2AERERCibqMLDw6mtrTVx\nmpGMyefn56dsogkICKC9vR0XF5dhy/dNTU2jLvGYmrH16+7uprGxcdhgsXXrVlxdXbGxsSEkJMQs\n6gfjZwRYvnw5d+7cISsrC7VajZeX15htHBwclE8j06GGMHo+gJcvX5KZmUl2djZqtRqAwMBAFi9e\nDEyPPgij53N3d2fjxo2oVCrmz5/PnDlzaGpqsqj6wcAyfUBAgHJsjmPoRP7OP1gXU/VBi52cg4KC\nKC4uBqCqqgo3NzccHR0B8PLyor6+XvlGVlZW4uPjg06nIy8vj4yMDGV5WwjBrl276OjoAAZ+6AZ3\nWk4lY/JlZ2fz6NEjYGCH4uDk5uvrS3l5OTCwJBwcHDwFiYYzJh9ATU0Nvr6+ynU6OzuJiYmht7cX\ngLKyMrOoH4yfESA2Npa2tja6u7t5/vw5gYGBY7ZZuXKlcn461BBGz9fZ2cmZM2fIyspSdmYDJCQk\noNPpgOnRB2H0fA8fPuT69evAwLJpW1sb7u7uFlM/GJiYZs2apSzxmusYOhFvb2/0ej1fvnyhv7+f\n58+fExQUZLI+aNH/lSo9PZ3y8nJUKhXJyclUV1ejVquJiIggLy+PwsJCrK2tCQgI4MiRI5w/f57H\njx/j6empXOP69es8ffqUnJwc7O3tcXd35/Tp09jb209hsgGTzdfY2Mjhw4cRQtDf36/8CkBdXR1J\nSUn8+fMHf39/ZVPcVJtsPoDi4mJev349bFn75s2bPHjwADs7O5YsWcLJkydRqVRTFWuY8TKWlJRw\n5coVVCoVe/bsYfPmzaO2WbRoEc3NzSQmJvL79288PT1JSUlRVn6m0mTz3bt3j8uXLw/bQ5CWlsbn\nz585e/Ys9vb2ODg4kJKSgqur6xQmGzDZfHq9nkOHDtHR0UFfXx/x8fGEhoZaTP1g4GH5woULw16Z\nFRUVmeUYWllZSVpaGg0NDdjY2ODu7k54eDje3t5ERERQVlZGeno6AOvWrVOW4k3RBy16cpYkSZKk\n6chil7UlSZIkabqSk7MkSZIkmRk5OUuSJEmSmZGTsyRJkiSZGTk5S5IkSZKZkZOzJEmSJJkZOTlL\nkiRJkpmRk7MkSZIkmZn/AP3D1ibMv0xUAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "\n",
+ "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " # YOUR CODE HERE\n",
+ " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n",
+ " \n",
+ " with tf.Session() as sess:\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ "\n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ "\n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ "\n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ "\n",
+ "\n",
+ " print ('The final loss is: ', final_loss)\n",
+ "\n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()\n",
+ " \n",
+ " "
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 551
+ },
+ "outputId": "29bc28d7-3c33-4b8d-bb54-0bf1f6631781"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500)"
+ ],
+ "execution_count": 125,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07239858\n",
+ "Loss after epoch 50 is 0.07207565\n",
+ "Loss after epoch 100 is 0.07175508\n",
+ "Loss after epoch 150 is 0.071436904\n",
+ "Loss after epoch 200 is 0.07112112\n",
+ "Loss after epoch 250 is 0.07080759\n",
+ "Loss after epoch 300 is 0.07049641\n",
+ "Loss after epoch 350 is 0.070187554\n",
+ "Loss after epoch 400 is 0.06988095\n",
+ "Loss after epoch 450 is 0.069576606\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.01730872\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XlcVPX+x/HXMGwii6CACpqKigqi\nmOWWa9jicm+raZmVWjeXdkvD0rqVWallVmZmt35l5a2s9NZVW7RuSVqKCrjjhisgi+www/n9gY7i\nBiIwMLyfj4cPHefM4fNxlLdzPud8j8kwDAMRERGpMZzsXYCIiIiUpnAWERGpYRTOIiIiNYzCWURE\npIZROIuIiNQwCmcREZEaxtneBZySkpJl16/v6+tBenquXWuoSo7eHzh+j+qvdnP0/sDxe6zs/vz9\nvS74nD45n+TsbLZ3CVXK0fsDx+9R/dVujt4fOH6P1dmfwllERKSGUTiLiIjUMApnERGRGkbhLCIi\nUsMonEVERGoYhbOIiEgNo3AWERGpYWrMIiQ10bx5r7NjxzbS0o6Tn59P06ZBeHv7MGPGa5Wy/9tu\nG0pAQCBOTqf/j/TWW+9d9n5/++0XunXryYkTmSxatICnnpp62fsUEZHqU65w3rlzJ+PHj+fee+9l\n5MiRpZ5bu3Ytc+bMwWw206dPHyZMmADAjBkz2Lx5MyaTiejoaCIiIiq/+ir20EOPAfD998vZsyeR\niRMfrfSvMWvWm3h4eFTqPj//fDFdulxFw4aNFMwiIrVQmeGcm5vLCy+8QI8ePc77/IsvvsiiRYsI\nDAxk5MiRXH/99aSlpbF//36WLFlCYmIi0dHRLFmypNKLt5eNG//i888/ITc3l4kTH+OJJyby3Xc/\nAfDMM09xyy3DaNeuPTNmPE9WVhZWq5VHH32S1q3blGv/gwdfe87+YmM3kJOTzYED+zl06CAPP/wE\nPXr0YsWK7/jyyyWYTCaGD7+LoqIitm6NZ9Kkh5ky5Vmef/4ZFi36mHXr1vHqq7NwdnbG3z+Ap5+e\nxo8/rmTLlk1kZKRz4MB+7rzzboYMuanK/txERKR8ygxnV1dXFi5cyMKFC895LikpCR8fH5o0aQJA\n3759iYmJIS0tjaioKABCQkLIzMwkOzsbT0/PChf63NpnWJ74TYVffz5DQ27iuZ4vVui1iYm7+eyz\npbi6up73+X//+zO6devJ0KE3sXfvHubOncUbb7xzOeWSnHyMWbPe5I8/1vLtt1/RqVNnPvzwfT76\n6DMKC4t46aXpzJw5h/fff5dZs94kMzPD9trp06cza9Y8AgMbM2fOK/zwwwpMJhOJibt5990POHgw\nienToxXOIiJnKbQWsmrfCiKtYQSZQ6rla5YZzs7Ozjg7n3+zlJQU/Pz8bI/9/PxISkoiPT2dsLCw\nUr+fkpJy0XD29fW46LqlHvVccXIylVXuJfGo51pq4fELLULu5eWOh8fpbRs08KBDh/YEBTUEwGQy\n2Z5zc3OhQQMPduxIIC0tjdWrVwFQUJB3zv7NZieefvoxzOaSvn19fXnzzTfPu7/69d3o0aMb/v5e\nhIa2pKAgj8zMZNq0aU1wsD8AixYttO23USNPzOYinJ2dcHGxYjKZCA8v+eTer19v/vzzTzp06MBV\nV11J48YN8PJyIS8v56ILsdcGtb3+sqi/2s3R+wPH6jE9L533NrzHvPXzOJR1iEFtBvHdnd9Vy9eu\nlhPCDMMoc5uy7vTxVOQ0noqcVlkl2Zy6G5a/v9cF74yVlZVPbm6h7fmMjFwMw2R7bBiG7dc5OXm2\n5x966AnCw0/P2s/ev9VazMsvv15q5pySknXe/eXkFODiUo+UlCzS03MoLLSQmZlPfn7hefebmppN\nZmYOFksxx4/nlNrn8eMnyM+3kJWVT2FhMSkpWeTm5mK1Ftv97mCX42LvoSNQf7Wbo/cHjtPjvsy9\nvLflHT7d9gm5lhzqu3jyQMQ4pkc9U6n9VdldqQICAkhNTbU9PnbsGAEBAef8fnJyMv7+/pfzpWo0\nk8lEfn4++fn57Ny5A4AOHcL59dc1AOzdu4fPP//ksvZ3Pldc0YIDB/aTm5tLQUEBjz46HsMwMJmc\nsFqttu28vb0xmUwcPXoUgE2bNtKuXfsKdCoi4rjWH1nHfStG0v3TSN6PW0ADtwZM7/Eim0Zt5cVr\nXqGpV9Nqq+WyPjkHBweTnZ3NwYMHady4MatXr2bWrFmkp6czb948hg8fTkJCAgEBAZc1b67pbrrp\nNh544B5atGhFaGhJ6N122x289NJzjB8/luLiYh59dNJl7e986tWrx5gxD/Loo+MBuOOOOzGZTERG\ndmH8+DFMnfqcbdsXXniB55+fitlsJigomGuvvY5Vq/5bsYZFRBzIwawk/vHDaP48ug6ATv6RjOs8\nkaGtbsLF7GKXmkxGGcec4+PjeeWVVzh06BDOzs4EBgYyYMAAgoODGThwIH/++SezZs0C4LrrrmPM\nmDEAzJo1i7/++guTycT06dNp167dRQux96EQRzkccyGO3h84fo/qr3Zz9P6gdvZ44MR+bvl2CAey\n9nPdFTcwIfIRujfpicl07jlOld3fxQ5rlxnO1cXeb2ht/Et1KRy9P3D8HtVf7ebo/UHt63Ff5l5u\n+XYIB7OTeOqqaCZdNeWi21dnOGuFMBERqXP2ZCZyyzdDOJxziOhu03j0yvKPHquDwllEROqUxIxd\n3PztEI7mHOHZHv/kocjKX/3xcimcRUSkztiVvpObvx1Mcu4xnu85g3GdJ9q7pPNSOIuISJ2wPW0b\nt347lJS8ZF665hXujxhn75IuSOEsIiIOb+vxBG5bNpTUvFRe7j2LMR0fsHdJF6VwvogjRw4zatRw\nQkNLLgMrLCzkrrvuoW/f/pe8r6++WkJGRgZ9+vTj11/XMGbMP8673anbPbq4lH1t3Z49u5kz59Vz\nbjPZt283OnbsZHvcsGFD3nnnrUuu+WyrV/9I//5R7Nq146I9iIjYS74ln2O5RzmWc4xjuUc4mnOE\nYznH+GTbh6Tlp/Fa3ze4J2y0vcssk8K5DM2bX2ELvxMnMrnvvrvo3r0Hbm7uFdpfmzahtGkTesHn\nT93usTzhfCGenp6Vcl/os33yyUf07x9VZg8iItWlwFrAa+tf5of9Kziac4T0gvTzbudkcmJOv3mM\n7HBPNVdYMQrnS+Dt7UPDho04fvw4//rXQpydXThxIoN//nMmr776EocPH8JisTB27INceeVV/PXX\net58czZ+fg1p2LARTZsGsXHjXyxd+m9efPHVi97uce7c+Sxb9jU//rgCk8mJ3r37MWLESJKTj/Hs\ns1NwcXGhdeu25a794MGDjB8/kUWLPgZgzJi7efHFV/jgg/do1MifHTu2cezYUaZNe5HQ0HYsXvwR\na9b8hMnkxIMPTmT79q3s3r2T6Ognue22O2w9/PTTDyxZshiz2UxoaHsefXQSixYtOO/tLUVEKtOe\njN088MNotqRsor6LJ0GeQYT7d6KxR2Ma129CoEdgyc/1m9DCpyWBHoH2Lrncak0413/uGdyWV+4t\nIwuG3kTOc+W/ZeSRI4c5cSKTgICSN9jb25vJk6eyYsV3NGzYiKefnkZGRgaPPPIgH330OQsWvMWz\nz75AmzZtmTTpYZo2DbLtKzc356K3e0xJSWbNmp94551FAIwbN4b+/aNYunQJ1157HcOGjeCTTz5k\n9+6dl/3nUFhYyJw5b/HNN1+yYsV3eHh4sGbNTyxY8CGHDx/ik08+ZMqUZ1m8+CNmzHiNjRv/OtlD\nLu+99zb/+teneHh48NRTj9meO/v2lgpnEalMX+z4nKd+fZycomzubHc3L/V+lfou9e1dVqWpNeFs\nLwcO7GfixJITB1xdXXnmmedtt9Ds0KHktpjx8VvYvDmWLVs2AVBQUEBRURFHjhyhTZuST7edO3eh\noKDAtt99+/bSvHkL3NzccXNzZ+bMOaW+7rZtCRw8mMRDD5XMdXNzczh69DD79u2lf/+Se2VHRnbl\njz/WnlNzdna2rWaAkJDWjB9/4flwp06RAPj7B7J1awI7d+6gQ4dwnJycCA5uxpQpz573dUlJBwgO\nbm67q1Zk5JXs3LkdgIiIzkDJzVGys7Mv+LVFRC5FdlE2T/86iSU7PsXTxYt3By7ilja327usSldr\nwjnnuRcv6VNuZTlz5nw2Z2cX28+jRo1m4MAbSj3v5HT6pl9nr5Lq5GTGMIov+HWdnV3o0aMXTz01\ntdTvL178ESaT08l9nv/155s5FxaeKPXYYrHYfn3qftKn6jSbnSguLntVV5OpdF8WSxFubm7n3aeI\nyOWKS93CA6vuJTFjN539I1lw3b9o6dPK3mVVicu6ZaSU6NAhnN9++wWA9PQ0Fix4G4BGjfw5cGAf\nhmEQG7uh1GvKut1jaGh7Nm7cQH5+PoZh8MYbsygoyKd58yvYvn0rgO0Qcnl4enqSnp6GYRgcP57K\n4cMHL7htaGh74uI2Y7FYSEs7ztNPlyxrd3ZgN2t2BQcPHiA3NweA2NiNhIZ2KHdNIiLlYRgGi+IW\ncOOXA0jM2M24Tg/xn1t+cNhghlr0ybkmGzAgio0b/+TBB0djtVoZPbrkkPIDD4znmWcm07hxE9uc\n+pSybvc4b957DBs2ggkT7sfJyYk+ffrh5ubO7beP4Nlnp/Drr6sJCWlT7hp9fHzo2vVqxo4dRevW\nbS56tnWTJk25/vpBTJz4AIZh8I9/TACgbdtQ7r9/FOPGPWzrYcKER3jiiYcwmZyIiOhMp06d+euv\ndZf05yciciF7MnYz7fdoVu1fQaN6jZg34F2uveI6e5dV5XRXqpNq291ULpWj9weO36P6q90cvT+o\n3B6P5Rxl1l+vsHjbR1iKLfQO7sc7175HYP3GlbL/itBdqUREpE46UZDJW7FzeW/LO+Racglp0Jro\nbtMZ0upv573HsqNSOIuIiN3lW/L5V/z7vLHhNdIL0gn0aMw/e73Mne3vxtmp7kVV3etYRERqjBMF\nmXy3Zzmv/fkyB7OT8Hb1YWq36dwfMQ4PFw97l2c3CmcREak2qXmp/HF4LX8c+Z2Yw2tJOB5HsVGM\nm9mN8Z0f5uEuj+Hn3tDeZdqdwllERKrMiYJMfti/kpiTgbwzfYftOVcnV65u3J2eTXtxd4f7CPIK\ntmOlNYvCWUREKt3xvOO8t+Vt3o97j6yTiyB5ONenX7MB9GjSix5Ne9E5oAvuzhW7iZCjUziLiEil\nOZZ7jPmb5vFh/CJyLTk0qufP+KunMqBZFB39O9XJk7sqQn9KIiJy2Q5nH+KFv95h4YaF5FvzaVK/\nKVO7T+Ou9vfU6RO7KkrhLCIiFZaUdYA3Nszm8+2fUFRcRDOv5jzc5XGGt7sLN7ObvcurtRTOIiJS\nIX8eXceI/9zGicJMWvq04tm+z3B9k7/jYnaxd2m1nsJZREQuWczh37nzu9vJt+Txap/XGdnhHpoE\n+jr8EqXVReEsIiKXZE3Sz9zz3xFYii0svO4jhoT8zd4lORyFs4iIlNsP+1YweuXdAHx4w2IGtrih\njFdIReh+ziIiUi7f7VnOvSvuwsnkxCeD/q1grkIKZxERKdPSXV8wduUoXM1ufD5kKX2b9bd3SQ5N\n4SwiIhf1+fbFjPthLB4u9fn30K/p0bSXvUtyeJo5i4jIOazFVlLyklm2+2ue+X0Kvm6+/HvoN3QK\niLR3aXWCwllEpI4qsBbwa9JqDmTt51D2IQ5nHzz58yGO5BzGUmwBoFG9RnwxdBlhjcLtXHHdoXAW\nEamD9p/Yx5iVo9iSsqnU7zuZnAj0aEwn/0iCPIMJ9mrGqLD7aOUTYqdK6yaFs4hIHbNy33+Z+NM/\nyCzI4Pa2w4m64jqaegYT5BlE4/pNdHOKGkDvgIhIHWEptjBz3Yu8GTsHd7M7c/u/w4j2I+1dlpyH\nwllEpA5Izk3mwR9G89uhX2np04pF139MeKOO9i5LLkDhLCLi4P44vJb7V93LsdyjDGo5lDcHvIO3\nm4+9y5KLUDiLiDgowzCYv/ktXoiZBsBzPV9iXKeJmEwmO1cmZVE4i4g4mEJrId/vWc6i+PdYdySG\nQI/GLLzuQ7o37Wnv0qScFM4iIg5iX+ZePt76IZ9t/5jUvFQArrviBmb3n0egR6Cdq5NLoXAWEanF\niqxFrNq/go8SFrEm6WcA/Nz9GNfpIUaF3UtIgzZ2rlAqQuEsIlLLGIZBXOpm/pO4jM+2f8Kx3KMA\ndG/Sk1Fh9zGk1d9xd3a3c5VyORTOIiK1gKXYwrojMXy/Zzn/3fsdB7OTAPB29eH+jg9yd9h9tPNr\nb+cqpbKUK5xnzJjB5s2bMZlMREdHExERYXvuxx9/ZP78+bi6ujJ48GBGjhzJunXreOSRR2jTpuRw\nStu2bXn22WerpgMREQeVZ8njl6TVfL93Oav2/Ze0/DQAfNwacFvbO7ix5RCubT4QDxcPO1cqla3M\ncF6/fj379+9nyZIlJCYmEh0dzZIlSwAoLi7mhRde4Ouvv6ZBgwbcf//9REVFAXD11Vfz5ptvVm31\nIiIO6GBWEu9ufovF2z4mpygbgECPxtwbNoZBrYbSq2lvXMwudq5SqlKZ4RwTE2ML3JCQEDIzM8nO\nzsbT05P09HS8vb3x8/MDoHv37qxdu5agoKCqrVpExAFtT9vGW7FvsHTXF1iKLTStH8R94WMZ1HII\nXQK74mRysneJUk3KDOfU1FTCwsJsj/38/EhJScHT0xM/Pz9ycnLYt28fQUFBrFu3jquvvpqgoCB2\n797Ngw8+SGZmJhMnTqRXL92cW0TkfNYd+YO3Yl9n5b7/AhDq244JkY9wS5vbcTW72rk6sYdLPiHM\nMAzbr00mEzNnziQ6OhovLy+Cg4MBaNGiBRMnTuTGG28kKSmJUaNGsWrVKlxdL/yXzNfXA2dncwVa\nqDz+/l52/fpVzdH7A8fvUf3Vbmf2V2wU8/2u73nl91f47cBvAPQI7sGUa6YwpO2QWvspuS69h1Wp\nzHAOCAggNTXV9jg5ORl/f3/b46uvvppPP/0UgNmzZxMUFERgYCCDBg0CoHnz5jRq1Ihjx47RrFmz\nC36d9PTcCjdRGfz9vUhJybJrDVXJ0fsDx+9R/dVup/orshbxze6veCv2DbalbQVg4BXX81DkY3Rr\n0gOTycTx1Bw7V1sxdeU9rMz9XUiZ/zXr1asXK1euBCAhIYGAgAA8PT1tz48dO5bjx4+Tm5vL6tWr\n6dGjB8uWLWPRokUApKSkcPz4cQIDtTqNiNRdeUV5LIp7jx6fdmHCTw+wM30Ht7YZxpo7Ylg8+Au6\nN+2pNa/FpsxPzl26dCEsLIzhw4djMpmYPn06S5cuxcvLi4EDBzJs2DBGjx6NyWTigQcewM/PjwED\nBjBp0iR++uknioqKeO655y56SFtExFFlFmTwr/j3WRg3n5TcFNzN7owOv59xnR/iCu8W9i5PaiiT\nceYQ2Y7sfShEh2NqP0fvUf3VfAXWArILs8kuyuJEQSZLd33JRwkfkF2UhY+bD/eF3c/9EePw9/Av\ne2e1kCO8hxdTnYe1tUKYiMgl2pW+k+fXPkNS1gGyi7LJLswiuyibouKic7YN8Ajk8a5P8UTfhyk4\nocPWUj4KZxGRcjIMg8Xb/o9nfptMriUXb1cfvFy9CPAIpJVrCPVdvPBy9cLTxRNPV0/CG0Zwa9th\nuDu74+3mRQqO+6lSKpfCWUSkHDLy03nil0dYnvgNPm4NWHTtuwwNucneZYmDUjiLiJThjyMxjP9h\nLAezk+jepCfvRC0k2OvCl4aKXC6Fs4jIBViKLby+4TVm//UKAE9dFc2jV07C2UnfOqVq6W+YiMh5\nHMxKYtyPY1l3JIZgz2a8M/B9ujfpYe+ypI5QOIuIAIXWQrYejyc2eSObkjfy/d7/kFmQwd9CbmZW\n3zdo4O5r7xKlDlE4i0idU2wUsyt9J7HJG9h0MozjU+MoLC60bePt6sPr/d7izvZ3a+UuqXYKZxGp\nU7ILs7jnv3fyv0O/2H7PxcmFDg3D6RzQhciALkQGXElb31DMTva9GY/UXQpnEakzsgpPMPw/t/Ln\n0XX0DurLoFZDiQzoQoeG4bg7u9u7PBEbhbOI1AmZBRncsfxmNiZv4JY2t/PWtQt01rXUWPqbKSIO\nLz0/jduX38SWlE0MCx3B3P7v6JC11Gi1827eIiLllJqXyi3fDmVLyiZGtr+HNwfMVzBLjadwFhGH\nlZybzC3fDibheBz3ho1hVr+5OJn0bU9qPv0tFRGHdDTnCDd/M4jtadt4IGIcr/SZo2CWWkN/U0XE\n4RzKOsjfv7mRXRk7Gd/5YV7oNVPXKkutohPCRMRhJGbs4vPtn/Lpto9JyUvm0S6TeLrbswpmqXUU\nziJSq2UVnuDb3V/z2fZP+PPoOgC8XL2Z1uMFJnR+WMEstZLCWURqnWKjmN8P/Y/Ptn/Cd3uWkWfJ\nw4SJvsH9Gd7uLga1Gko953r2LlOkwhTOIlKr/H7ofzyyegIHTuwDoIV3S4a3u4thoSN0j2VxGApn\nEakVDMNg4Zb5TF87FZPJxIh2IxnRbiTdmvTQoWtxOApnEanx8ix5PPnLo/x7x2c0qufPB9d/TPem\nPe1dlkiVUTiLSI12KOsg9664i80psUQGdOFfNyymqWeQvcsSqVIKZxGpsWIO/86YlXeTmpfKiHYj\neaXPHN09SuoEhbOI1DiGYfBB/Hs8+/vTALzcexajw+/XbFnqDIWziFSrXw+uIT41DjezG+5md9yc\n3XAzuxOY7kt+TjFuZnc+2/Yxn27/mEb1GrHo+o/p0bSXvcsWqVYKZxGpFsm5yUz931N8m7i0XNt3\n9o/kXzcsJsgruIorE6l5FM4iUqUMw2DJjk+Z9vvTZBRkcGXgVYzv/BDFRjH5lnwKrAUUWPNxdofj\nmZkUWAto4ObL6I73ayERqbMUziJSZfZl7uWJXx7hfwfXUN/Fk5d7v8a9YWPPez9lf38vUlKy7FCl\nSM2jcBaRSmcptvDelvm8sv5F8ix5RDW/jlf7vq4VvETKSeEsIpUqPjWOx1dPZFNKLA3dG/J6/7e4\nufVtOtNa5BIonEWkUliLrcyLfZ1X/5yBpdjC7W2H889eL9OwXkN7lyZS6yicReSy7T+xjwk/PsD6\no3/QuH4T3uj/FgOaD7R3WSK1lsJZRCrMMAz+veMznv7fk2QXZTE05CZm9X0DX3c/e5cmUqspnEWk\nQtLz03jyl8dYlvg1ni5ezBvwLsNCR2i2LFIJFM4icsl+SVrNQz8/yNGcI1zduDtvR73HFd4t7F2W\niMNQOItIuR3KOsi7W95mwea3cXZyJrrbNB6KfOy81y2LSMUpnEXkgo5kH+b3w//j90MlP/ad2AtA\nSIPWzI96n84BXexcoYhjUjiLiE1a/nFWH/iJtYd/47dDv7I3c4/tOW9XH25oMYhrgvpwV4d7qO9S\n346Vijg2hbNIHWcptrD6wI98tn0xK/d9T1FxEQBert5cd8UN9AzqzTVBvQlr2FGHr0WqicJZpI7a\nmbaDz7Z/whc7Pyc59xgA7f06cGvbYfQJ7kfHRp0UxiJ2onAWqUMyCzL4ZvdSPt/+CRuO/QWAj1sD\n7gsfy4h2I+nkH6lLoURqAIWzSB1QbBTzydaPeOGP6WQWZOBkcmJA8yhGtBvJ9S0G4e7sbu8SReQM\nCmcRB7czbQdP/PIw647E4OnixZSrn2FEu5E08Wxq79JE5ALKFc4zZsxg8+bNmEwmoqOjiYiIsD33\n448/Mn/+fFxdXRk8eDAjR44s8zUiUvXyLfnM3TibNzfOoai4iMGt/saMa15VKIvUAmWG8/r169m/\nfz9LliwhMTGR6OholixZAkBxcTEvvPACX3/9NQ0aNOD+++8nKiqKAwcOXPA1IlL1fj/0Pyb98giJ\nGbtpUr8pM/vM5saWg+1dloiUU5nhHBMTQ1RUFAAhISFkZmaSnZ2Np6cn6enpeHt74+dXssh99+7d\nWbt2LUlJSRd8jYhUnfT8NJ5f+yyfbv8YEybu7/ggT3d7Fk9XL3uXJiKXwKmsDVJTU/H19bU99vPz\nIyUlxfbrnJwc9u3bR1FREevWrSM1NfWirxGRyrcrfScvxEyn56dX8un2jwlr2JH/3voTL/V+VcEs\nUgtd8glhhmHYfm0ymZg5cybR0dF4eXkRHBxc5msuxNfXA2dn+15T6e/v2N/EHL0/cPwez+wvIz+D\nJfFL+HDzh/xx8A8AGrg34JWoV3is+2O4mF3sVWaF1aX3z1E5eo/V1V+Z4RwQEEBqaqrtcXJyMv7+\n/rbHV199NZ9++ikAs2fPJigoiIKCgou+5nzS03MvufjK5O/vRUpKll1rqEqO3h84fo/+/l4cPZbB\n/w79wufbP+H7Pf8h35p/3suiMtLygXx7l3xJ6sL758j9geP3WNn9XSzoyzys3atXL1auXAlAQkIC\nAQEBpWbHY8eO5fjx4+Tm5rJ69Wp69OhR5mtE5NIkZuxi6k9T6fpJR4Ytv4mlu74k2KsZz3R/jti7\nt/L5kKX8vfUtul5ZxEGU+cm5S5cuhIWFMXz4cEwmE9OnT2fp0qV4eXkxcOBAhg0bxujRozGZTDzw\nwAP4+fnh5+d3zmtE5NJk5Kfzze6lLNnxKRuO/QmUrHd9d4f7GN7uTroGXq3VvEQclMkoz0C4Gtj7\nUIgOx9R+jtCjpdjCmqSfWLL9M1bs+44CawFOJif6Bvfn/qvG0KvRtdRzrmfvMquEI7x/F+Po/YHj\n91idh7W1QphIDZCSm8LCLfP5dPvHtptQtPUNZVjondze9g6aeDZ1+G98InKawlnEjpKyDvDOpjdZ\nvPX/yLfm0+DkTSiGh95F54AuOmwtUkcpnEXsYGfaDubFvs5Xu/6NpdhCM6/mTIh8hBHtRjrsYWsR\nKT+Fs0g12pS8kbkb5/D9nuUYGLT1DeXhLo9zc+vbauV1ySJSNRTOItVgU/JGZqz7J2uSfgYgMqAL\nj3SZxA0tB+FkKvOKRhGpYxTOIlVoT8ZuXl73It8mLgXgmqA+PNLlCfoE99M8WUQuSOEsUgWO5R5j\n9p8z+WTbR1iKLUQGdOGZ7s/TO7ivvUsTkVpA4SxSibIKT/B27Fze3fw2uZZcQhq0JrrbNIa0+rs+\nKYtIuSmcRSpBkbWIf8Uv5PXF/NO7AAAgAElEQVQNr3E8/ziBHo15vtcM7mx3t070EpFLpnAWuUx7\nMhMZ98MYYpM34uXqTXS3adwfMY76LvXtXZqI1FIKZ5EKMgyDf+/4jCn/m0ROUTa3tx3OC9e8jJ97\nQ3uXJiK1nMJZpAJOFGTy1K+Ps3TXF3i6eDE/6n1ubTvM3mWJiINQOItcor+OrufBH8dy4MQ+rgzs\nyvyoRbTwaWnvskTEgSicRcrJWmzlzY1zePXPGRQbxTx25SQmdX1aJ3yJSKVTOIuUw670nTz5y6Os\nPfwbTesH8U7UQnoGXWPvskTEQSmcRS5g/4l9fLv7a77Z/RXxqVsAGNRyKK/3n4evu5+dqxMRR6Zw\nFjnD4exDfLv7a77d/RUbkzcA4OLkwsArrueO0DsZGnKTFhMRkSqncJY6L9+Sz793fMYXOz9n3ZEY\nAMwmM32D+3Nzm9sY1HIIDdx97VyliNQlCmeps7KLsvm/hH8xf9M8juUexYSJnk2v4abWtzIk5O80\nqtfI3iWKSB2lcJY6J7Mgg/fjFrBwy3zS8tOo7+LJxMhHub/jgzTxbGrv8kREFM5Sd6TmpbJg89t8\nEL+QrMITNHBrwJNXPc3Yjv/QCV4iUqMonMUhGYZBcu4x9mbuYW/mHmKTN7Bkx6fkWfJoVM+fR3v8\nk/vCxuDp6mXvUkVEzqFwllovPT+N/+xZxtHCJBKObGdv5h72n9hLriW31HZBnsFMjHyEO9uPop5z\nPTtVKyJSNoWz1Goxh3/nwR/GcCTnsO336rt40qpBa1p4t6SlTyvbj6sad8PV7GrHakVEykfhLLWS\ntdjKnA2vMvuvVzBh4vGuT3FrxN/xKQ7Ev56/rkUWkVpN4Sy1zpHsw4z7cSxrD/9GsGcz5g9cRLcm\n3fH39yIlJcve5YmIXDaFs9Qqq/b9l4d/HkdafhqDWg7ljf5vaYEQEXE4CmepFQqsBbwYM50FW97B\nzezGK33mcG/YGB2+FhGHpHCWGi8xYxf/+GEMW1I20aZBW9677kPCGoXbuywRkSqjcJYa63jecV7f\n8Cr/in+fouIi7mx3Ny/1fpX6LvXtXZqISJVSOEuNk2fJY+GW+czdOIeswhM0927B9B4vMDTk7/Yu\nTUSkWiicpcawFlv5947PeGX9SxzOOYSfux8v9prJPeFjcDO72bs8EZFqo3AWuzMMg58P/MA/Y6ax\nLW0r7mZ3Ho58nIe6PIqPWwN7lyciUu0UzmJXmQUZPLDqPlYn/YQJEyPajeSpq6IJ8gq2d2kiInaj\ncBa7ySzIYNjym4hN3kif4P483/MlnYUtIoLCWezkREEmdyy/mdjkjdwReidv9H8bs5PZ3mWJiNQI\nTvYuQOqeEwWZDFt+ExuTNzAsdISCWUTkLApnqVYnCjK54z83szF5A7e3Hc7c/u8omEVEzqJwlmqT\nVXiCO/5zCxuO/cXtbYfz5oD5CmYRkfNQOEu1yCo8wbDlN7Ph2J/c1vYOBbOIyEUonKXKZRWe4I7l\nt7Dh2J/c2mYY8wa8q2AWEbkIna0tFWYYBt/v/Q8/7FuB2cmMs5MzLk4uuDi54uLkgrOTM65mV1bu\n+54Nx/7ilja389a1CxTMIiJlUDhLhRzJPszk/z3Bir3flWv7W9rcztvXvqdgFhEpB4WzXJJio5iP\nt37IP2OmkVV4gl5NezO95wt4uXpRaC3CUlxEUXERhcUlvy60FlLPuR5XN+6uYBYRKadyhfOMGTPY\nvHkzJpOJ6OhoIiIibM8tXryYZcuW4eTkRHh4OFOnTmXp0qXMnTuX5s2bA9CzZ0/GjRtXNR1ItUnM\n2MXjax4m5vDveLv6MKffPO5qPwqTyWTv0kREHEqZ4bx+/Xr279/PkiVLSExMJDo6miVLlgCQnZ3N\nokWLWLVqFc7OzowePZpNmzYBMGjQICZPnly11Uu1KLIW8c6mN5n110wKrAUMajmUmX1m0bh+E3uX\nJiLikMoM55iYGKKiogAICQkhMzOT7OxsPD09cXFxwcXFhdzcXDw8PMjLy8PHx6fKi5bqUWQtYt3R\nGJ797WkSjscR4BHIy71n6b7KIiJVrMxwTk1NJSwszPbYz8+PlJQUPD09cXNzY8KECURFReHm5sbg\nwYNp2bIlsbGxrF+/njFjxmCxWJg8eTIdOnS46Nfx9fXA2dm+M0l/fy+7fv2qVlZ/BZYC1h9azy/7\nf+GX/b+wNmktuUW5AIyJHMNrA1/Dt55vdZRaYXX9Pazt1F/t5+g9Vld/l3xCmGEYtl9nZ2ezYMEC\nVqxYgaenJ/fccw/bt2+nU6dO+Pn50a9fP2JjY5k8eTLLly+/6H7T03MvvfpK5O/vRUpKll1rqErn\n688wDNYdieGXg6uJOfw7G479SYG1wPZ8qG87ejTtxc1tbqNH015YsiElu+b+GdXF99CRqL/az9F7\nrOz+Lhb0ZYZzQEAAqamptsfJycn4+/sDkJiYSLNmzfDz8wOga9euxMfHc9tttxESEgJAZGQkaWlp\nWK1WzGadrVtTHDixnym/PsGPB1YBYMJEWKOO9GjSkx5Nr6F70540qtfIzlWKiNRNZYZzr169mDdv\nHsOHDychIYGAgAA8PT0BCAoKIjExkfz8fNzd3YmPj6dv374sXLiQJk2aMGTIEHbu3Imfn5+CuYYo\nshaxYMs7vPbnDPIsefQO7scDEePo1rg7Ddxr9iFrEZG6osxw7tKlC2FhYQwfPhyTycT06dNZunQp\nXl5eDBw4kDFjxjBq1CjMZjORkZF07dqV4OBgnnzyST7//HMsFgsvvfRSdfQiZfjr6Hom/fIoW4/H\n06heI2b3e5Nb2wzTpVAiIjWMyThziGxH9p5TOPKsJLMggzmbX+bdv97FwGBk+3t4tsfz+Lr72bu0\nSuXI7yGov9rO0fsDx++xRs2cpfYyDINliV8z9bfJJOceo61vKLP6zqV70572Lk1ERC5C4eygNiVv\n5Pm1z/L74f/hZnbjxf4vcm/bB3E1u9q7NBERKYPC2cHsy9zLy+v+yde7vwJg4BXX88I1M+nWurND\nH24SEXEkCmcHkZZ/nNf/eo0P4hdSVFxEZ/9IpvV8gWuC+ti7NBERuUQK51ouz5LHwi3v8ubGOZwo\nzKS5dwumdpvG31vfgpPJyd7liYhIBSica6kCawFf7ljCrL9mcij7IL5uvrzQ62XuDR+Lm9nN3uWJ\niMhlUDjXMtmFWXy89SPe3fwWR3IO42525+HIx3moy6P4uDWwd3kiIlIJFM61RGpeKu/HvcsHce+R\nUZBBfRdPxnV6iAc7TaCJZ1N7lyciIpVI4VzDJWUdYP6meSze9n/kWfJo6N6QKVc/w33hYx1uERER\nESmhcK6BcotyWZP0M9/u/oplid9gNawEezZjQuTDjGh3Nx4uHvYuUUREqpDCuYY4UZDJD/tX8t2e\n5fx84AdyLSW30Az1bcdDXR7j5ta34WJ2sXOVIiJSHRTOdpSSm8LKfd/z3Z5l/HpwDUXFRQCENGjN\n4JZ/Y3CroXQO6KIbU4iI1DEKZzvYl7mXORte5Ysdn2M1rACEN4pgcKuhDG71N0J92ymQRUTqMIVz\nNTpwYj9vbJjF5zsWYym2EOrbjhHt72ZQyyG08Glp7/JERKSGUDhXg0NZB3lj42w+3fZ/FBUX0bpB\nG5686mn+FnIzZiezvcsTEZEaRuFchY7mHGHuxtl8nPAhhcWFtPRpxaSuU7ilze0KZRERuSCFcyXK\nLMggNnkjscc2EJu8gdVJP1FgLaC5dwsmdZ3MbW3vwNlJf+QiInJxSooKKrAWsDU1no3Jf7HxZBjv\nzthVapuWPq14KPIx7gi9U5dBiYhIuSmcy6HQWsi24wlsTtnE5pRYNqdsYtvxBNulTwBert70Ce5P\nl4AriQy8ki4BVxJYv7EdqxYRkdpK4XweRdYivt79JeuO/MGWlE1sPR5fKojdzG50bBRBp4BIugR0\npUtgV0IatNYtGkVEpFIonM/y59F1TFrzKNvSEgBwdXIlvFFHIvwj6ewfSURAZ9r5ttdhahERqTIK\n55My8jN46pdJfJTwAQYGd7UfxX3hY2nn1wFXs6u9yxMRkTqkzoezYRh8u3sp02Ke5mj2Udr6hjKr\n71y6N+1p79JERKSOqtPhvC9zL5N/fZzVST/h7uxOdLdpjO/8sD4pi4iIXdXJcM4pymFR3AJm/TmT\nfGs+fYP78/7N7+FjDbR3aSIiInUnnLOLsvlx30qW7/mWn/avIteSS6N6/rxxzdvc3Po2Avy8SUnJ\nsneZIiIijh3O2YVZrNq/gmW7v+HnAz+Qb80HSm7J+PeQm3mw00QauPvauUoREZHSHDKcY49t4PWN\ns1h94EcKrAUAtGnQlqGtb+JvITfT3q+DbskoIiI1lkOG84It77Bi73e082vP0JCbGBpyE+382tu7\nLBERkXJxyHB+re/rPN3tWa7wbmHvUkRERC6ZQ4azl6s3Xq7e9i5DRERqI8PA6dhRnOO34BxX8sO8\nNR6G3Q6PR1dLCQ4ZziIiIuVSXIx5byLO8XEng3gzznFbcEpNKb2Znx80alRtZSmcRUSkbigowHnH\nttMhHB+HOSEep5zsUptZmzWn4MYhWDpGYOnYCUt4R4qbBuEf4A3VdMmtwllERByO6UQmzgnxtk/C\nznFbMO/cjslisW1jmM1Y27SlMDwCS3hESRiHd8Tw9bNj5SUUziIiUnudmg+fCuH4OJzjNmPev6/0\nZvXqYenUGUt4p5OfiCOwtOsA9erZp+4yKJxFRKR2ODUfjttyxqHpLTilppbezM+Pwj79bZ+ELR07\nYQ1pDWaznQq/dApnERGpeQoKcN6+1fZJ2DluC84J8Zhyc0ptdqH5MLV8oSmFs4iI2JUpM6P0fDg+\n7vzz4bahJbPhM+fDDRxzCWaFs4iIVA/DwOnoEduZ0rYTtQ7sK71ZvXpYOkWeDOCaPx+uCgpnERGp\nfMXFmPcknvFpeEvZ8+GTYVzb5sNVQeEsIiKX5+R8mH078Vy7ruRT8fnmw82voGBQj1KfiIubNK31\n8+GqoHAWEZFyK2s+XI+z5sOngtiB58NVQeEsIiLnOnM+fOrSpfi4c+fDHh62+XC9nt1Ib9G2ZD7s\n7m6fuh1EucJ5xowZbN68GZPJRHR0NBEREbbnFi9ezLJly3ByciI8PJypU6dSVFTElClTOHz4MGaz\nmZdffplmzZpVWRMiInIZrNaS+XD8GdcPJ8SdOx9u2JDCvv1PfyLu2AlrqxDbfLievxeWalre0tGV\nGc7r169n//79LFmyhMTERKKjo1myZAkA2dnZLFq0iFWrVuHs7Mzo0aPZtGkTe/fuxdvbm9mzZ/Pb\nb78xe/Zs3njjjSpvRkREypCff+71w1sTLjwfPrmIh+bD1avMcI6JiSEqKgqAkJAQMjMzyc7OxtPT\nExcXF1xcXMjNzcXDw4O8vDx8fHyIiYnhpptuAqBnz55ER1fPLbZEROQ0U2bG6RA+eemSedeO81w/\n3K7UalqW8I4YPg3sWLmUGc6pqamEhYXZHvv5+ZGSkoKnpydubm5MmDCBqKgo3NzcGDx4MC1btiQ1\nNRU/v5KFw52cnDCZTBQWFuLq6lp1nYiI1FWGgdORw6XuP3zB+XDnLqVW09J8uGa65BPCDMOw/To7\nO5sFCxawYsUKPD09ueeee9i+fftFX3Mhvr4eODvb97o2f38vu379qubo/YHj96j+ardK6c9qhV27\nIDa25MemTSU/nzUfplEjGDgQIiNtP0ytW+NiNuNy+VVckN7DylFmOAcEBJB6xpuenJyMv78/AImJ\niTRr1sz2Kblr167Ex8cTEBBASkoK7dq1o6ioCMMwyvzUnJ6eezl9XDZ/fy9SHPhEBkfvDxy/R/VX\nu1Wov1Pz4VMnacVtwXlbAqbc0t8vrc1bYBncs9Sh6eLGTc6dD6dV7fdZvYeXvr8LKTOce/Xqxbx5\n8xg+fDgJCQkEBATg6ekJQFBQEImJieTn5+Pu7k58fDx9+/bFzc2NFStW0Lt3b1avXk23bt0qrRkR\nEUdkykgvmQufOjQdvwXzzh2YrFbbNoaz87nz4bBwzYcdUJnh3KVLF8LCwhg+fDgmk4np06ezdOlS\nvLy8GDhwIGPGjGHUqFGYzWYiIyPp2rUrVquVtWvXMmLECFxdXZk5c2Z19CIiUvMZBk6HD511t6U4\nzAf2l97Moz6WLl1Lry8d2l7z4TrCZJRnIFwN7H0oRIdjaj9H71H91UJWK+bE3TjHbcZ7zw4K1/2F\nc/xmnNLSSm1W3KjRyQDuZFtj2tqiVa1bX9oh38Mz1KjD2iIiUg75+ThvSzh9k4fzzIddAesVLSjo\n2fvkYemSQC4ObKzrh6UUhbOIyCWyzYfPWE3rovPhjhF4XtOd1OAQDG8fO1YutYXCWUTkQk5dP3zm\n2dLxWzAnHSi92Znz4VOHpkPbg5ubbRtPfy8MBz7kK5VL4SwiAqfnw2cu5JGwBafjx0ttVtzIn8L+\n156xvnQE1pYh4ORkp8LFESmcRaTuycs74/rhkzPi810/fEULCnpco/mwVDuFs4g4NFNGum05y5I1\nprdg3rXzovNhS3iErh8Wu1I4i4hjOHX98JlnS59nPlxc3xPLlVede/3wGfNhEXtTOItI7WO1Yt69\n69z58DnXD5+cD586SSu8o+bDUisonEWkZsvLO3398MkQdt6agCkvr9RmtuuHzzg0rfmw1FYKZxGp\nMUzpaedeP1zWfPjU+tK6flgciMJZRKqfYeB06GCp9aXZGkejA5oPi4DCWUSq2qn5cNzm05+KzzMf\nJiDg9Hz45KVLmg9LXaVwFpHKk5tbMh8+FcLxm3HetvXc+XCLlhT06lPq+uGG4W3I1ApaIoDCWUQq\nyJSeVnoRj1PXDxcX27YxXFywhLbHekYIWzqEaT4sUgaFs4hc3Kn58KmTtOLjSoL4YFKpzYrre2K5\nqhtFJ0PYGt4RS9t2mg+LVIDCWUROO3M+fGpVrfjNOKWnl9qs2D+AwgFRWDp2Kgnj8AiKW7TUfFik\nkiicReqqcs6HLS1bUdi73+lD06euHxaRKqNwFqkDTGnHzwjhi8+HbXdaOrW+tJe3HSsXqZsUziKO\nxDBwOphU6iYPznFbMB86WGqzs+fDlvAIrKHtwNXVToWLyJkUziK1lcVS+vrhk5+Iz54PWwMCKbh2\nINbwCIo6RmAN74i1RSvNh0VqMIWzSG2QmwvrtuL+a4ztJC3nrQmY8vNLbXZqPmw5GcJF4Z0wAgPt\nVLSIVJTCWaSGMaUdP/f+w7t3QXExXie3OXs+bAnvhDUsTPNhEQehcBaxl1PzYdv1wyWBfM582NOL\noqu743rVlZxo3V7zYZE6QOEsUh3OnA+fcca0U0ZGqc1OzYdt9x8O62i7ftjf34sCLW8pUiconEUq\nW24uzlvjz71++Oz5cKsQCvsOOL2+dHgnjIAAOxUtIjWJwlnkMlxoPnzO9cPtOpyeD4dFYA0Px/D0\nusieRaQuUziLlIdh4JR0oNQhaee4LZgPHyq12an5sO0mD2EdNR8WkUumcBY5m8WCedfO0/PhhLjz\nz4cDG1MQdR2W8Ihz5sMiIpdD4Sx1W05OyfrSpz4Rx52cDxcUlNrMNh8+uba0JTxC82ERqTIKZ6kz\nTMePn/Fp+ORh6cTdpefDrq4l8+EzTtKyhoVpPiwi1UrhLI7HMHA6sP/c9aWPHC61WbGXN0XdepwM\n4pPrS7cN1XxYROxO4Sy1W1GRbT5M4nZ8/tyAc3wcTpllzIfDIyi+ooXmwyJSIymcpfbIySm5fjju\n9NnSzttLz4ddTCasrUIo7Kf5sIjUXgpnqZFMqamnAzh+8+n5sGHYtrHNhztGYAnviFfvHhxv2lLz\nYRGp9RTOYl+n5sOnQvjkqlrnnQ/36FUyHw4vuYbY2jYUXFxs23j5e2FoeUsRcQAKZ6k+Z8yHT38q\njsPpRGapzayNm1Aw8Hrb2dKW8I4l82GTyT51i4hUM4WzVI1yzIcNkwlrSGsKB1xbEsInZ8SGv78d\nCxcRsT+Fs1w2U2rqyU/DcRefD7cPs62kZenYCUuHMPD0tGPlIiI1k8JZyq+882Fvn5L58BlBfPZ8\nWERELkzhLOdXVIR5546ST8QJceWbD4eVXEOs+bCIyOVROAtkZ+O8NaF0EF9oPnxtlC2ENR8WEaka\nCuc6xjYfPuPQ9DnzYTe3M64fPvlD82ERkWqjcHZUZ82H2bEVv42xF58Pn7p+uE1bzYdFROxI4ewI\nzpwPx285edb0ufNhmjSl4LobTi7kUXLpUnHzKzQfFhGpYcoVzjNmzGDz5s2YTCaio6OJiIgA4Nix\nY0yaNMm2XVJSEk888QRFRUXMnTuX5s2bA9CzZ0/GjRtXBeXXQdnZOCfEnwzhM64fLiy0bXK++XCD\n/r1Iw92OhYuISHmVGc7r169n//79LFmyhMTERKKjo1myZAkAgYGBfPzxxwBYLBbuvvtuBgwYwMqV\nKxk0aBCTJ0+u2uodnCkl5azVtLZg3pN47ny4Q1jJdcNhJ+9B3CEc6tcvvTN/L9DSliIitUKZ4RwT\nE0NUVBQAISEhZGZmkp2djedZJwd9/fXXXH/99dQ/OxSkbIaB0769pT8Nx23BfOxoqc2KfRpQ1POa\nUrc91HxYRMTxlBnOqamphIWF2R77+fmRkpJyTjh/8cUXfPDBB7bH69evZ8yYMVgsFiZPnkyHDh0u\n+nV8fT1wdjZfav2Vyt+/Gu5mVFQEW7dCbCxs2nT65xMnSm8XHAxDhkBkpO2H0xVX4Goy4VrBL10t\n/dmZo/eo/mo3R+8PHL/H6urvkk8IM844pHpKbGwsrVq1sgV2p06d8PPzo1+/fsTGxjJ58mSWL19+\n0f2mp+deaimVyt/fi5RKPuxrys7CnJBgW9LSOW4Lzju2nTsfbt0GS9R1pa8fbtTo3B2mZle4lqro\nr6Zx9B7VX+3m6P2B4/dY2f1dLOjLDOeAgABSU1Ntj5OTk/E/a+GJNWvW0KNHD9vjkJAQQkJCAIiM\njCQtLQ2r1YrZbN9PxlXJlJxcaklL57jNmPfuqdh8WERE6rQyw7lXr17MmzeP4cOHk5CQQEBAwDmH\ntOPi4hg0aJDt8cKFC2nSpAlDhgxh586d+Pn5OU4wFxfjtH9fqZO0Ljgf7tX75CIeHU9fP+ysq9dE\nROTiykyKLl26EBYWxvDhwzGZTEyfPp2lS5fi5eXFwIEDAUhJSaFhw4a21wwdOpQnn3ySzz//HIvF\nwksvvVR1HVSlwkLMO7afXNLy5KHphHicskrPh61Ngyi4/sbTq2l1jKC4WXNdPywiIhViMs43RLYD\ne88p/N0hfU1M6UPTF5oPn3GThwvOh2sYR58FgeP3qP5qN0fvDxy/xxo1c3ZEtvnwyTstOcdthr17\n8L3QfPjUoWnNh0VEpBo4djifPR+OO3mjh/PMh+nXj9zQMM2HRUTE7hwyfVxX/pd6b889/3w4KPj0\nfLjjyfWlg5vhH+BNjgMfjhERkdrDMcP5h5W4rP8Da+s2FA68znaTB0t4BMYZJ66JiIjURA4Zztmv\nvU72S6+Am5u9SxEREblkTvYuoEqYTApmERGptRwznEVERGoxhbOIiEgNo3AWERGpYRTOIiIiNYzC\nWUREpIZROIuIiNQwCmcREZEaRuEsIiJSwyicRUREahiFs4iISA2jcBYREalhTIZhGPYuQkRERE7T\nJ2cREZEaRuEsIiJSwyicRUREahiFs4iISA2jcBYREalhFM4iIiI1jLO9C6hKM2bMYPPmzZhMJqKj\no4mIiLA9t3jxYpYtW4aTkxPh4eFMnToVi8XC1KlTOXDgAFarlaeeeoquXbty9913k5ubi4eHBwCT\nJ08mPDzcXm3ZXGp/S5cuZe7cuTRv3hyAnj17Mm7cOLZv385zzz0HQGhoKM8//7w92jnHpfY3f/58\n1q5dC0BxcTGpqamsXLmSAQMG0LhxY8xmMwCzZs0iMDDQLj2d7WI9/vjjj8yfPx9XV1cGDx7MyJEj\nL/iaI0eO8NRTT2G1WvH39+e1117D1dXVXm3ZVKS/V199lQ0bNmCxWPjHP/7Bddddx5QpU0hISKBB\ngwYAjBkzhn79+tmjpVIutb9169bxyCOP0KZNGwDatm3Ls88+6zDv3xdffMGyZcts28THxxMbG1tj\nv4cC7Ny5k/Hjx3Pvvffa/g6esnbtWubMmYPZbKZPnz5MmDABqKZ/g4aDWrdunfHAAw8YhmEYu3fv\nNoYNG2Z7Lisry+jfv79RVFRkGIZh3HfffUZsbKzx5ZdfGtOnTzcMwzB27txp3HrrrYZhGMbIkSON\nHTt2VG8DZahIf1999ZUxc+bMc/Y1cuRIY/PmzYZhGMbjjz9urFmzpho6uLiK9HempUuXGgsXLjQM\nwzD69+9vZGdnV1Pl5XexHq1Wq9GnTx/j+PHjhtVqNUaPHm0cOXLkgq+ZMmWK8f333xuGYRizZ882\nFi9eXM3dnKsi/cXExBhjx441DMMw0tLSjL59+xqGYRiTJ082fv7552rv4WIq0t8ff/xhPPTQQ+fs\ny1Hev7Nf/9xzzxmGUTO/hxqGYeTk5BgjR440nnnmGePjjz8+5/kbb7zROHz4sGG1Wo0RI0YYu3bt\nqrZ/gw57WDsmJoaoqCgAQkJCyMzMJDs7GwAXFxdcXFzIzc3FYrGQl5eHj48Pf/vb33j66acB8PPz\nIyMjw271l6Ui/Z1PYWEhhw4dsv2PuH///sTExFRPExdxOf1ZLBY+++yzc/4XXNNcrMf09HS8vb3x\n8/PDycmJ7t27s3bt2gu+Zt26dVx77bVA7XgPL9TfVVddxdy5cwHw9vYmLy8Pq9Vqtx4upiL9XYij\nvH9nevvttxk/fny1130pXF1dWbhwIQEBAec8l5SUhI+PD02aNMHJyYm+ffsSExNTbf8GHTacU1NT\n8fX1tT328/MjJSUFADc3NyZMmEBUVBT9+/enU6dOtGzZEhcXF9zc3AD46KOPGDJkiO31b775Jnfd\ndRfTpk0jPz+/eps5jw5XXOgAAAVfSURBVIr0B7B+/XrGjBnDPffcw9atW23/yE5p2LChbT/2VNH+\nAFatWsU111yDu7u77femT5/OiBEjmDVrFkYNWRTvYj36+fmRk5PDvn37KCoqYt26daSmpl7wNXl5\nebZDaLXhPbxQf2az2Xbo88svv6RPnz62ccQnn3zCqFGjeOyxx0hLS6v+hs5Skf4Adu/ezYMPPsiI\nESP4/fffARzm/Ttly5YtNGnSBH9/f9vv1bTvoQDOzs6lvk+cKSUlBT8/P9vjU/1X179Bh545n+nM\nb8jZ2dksWLCAFStW4OnpyT333MP27dtp164dUDLPTEhI4N133wVg1KhRhIaG0rx5c6ZPn87ixYsZ\nM2aMXfq4kPL016lTJ/z8/OjXrx+xsbFMnjyZ999//4L7qUku5f376quvSs3NH374YXr37o2Pjw8T\nJkxg5cqV3HDDDdXeQ1nO7NFkMjFz5kyio6Px8vIiODi4zNdc7Pdqgkvp78cff+TLL7/kgw8+AODv\nf/87DRo0oH379rz33nu89dZbTJs2rVrrL0t5+mvRogUTJ07kxhtvJCkpiVGjRrFq1aoL7qcmuZT3\n78svv+Tmm2+2Pa4N30Mrqqr+DTrsJ+eAgIBS/5NLTk62/S8uMTGRZs2a4efnh6urK127diU+Ph6A\nL774gp9//pl33nkHFxcXAAYOHGg7iWrAgAHs3Lmzmrs5V0X6CwkJsZ1EExkZSVpaGr6+vqUO3x87\nduy8h3iqW0Xfv9zcXI4ePVrqm8VNN91Ew4YNcXZ2pk+fPjXi/fv/9u7fJZ04juP48yiIs24qOlCJ\ncKqWcAlMIghsaOhviGqsrR9TNYVYEkEFiTm0hC0RUYEROAQtOlo01JIFFbioBJXkdzg68IsVNeQp\n78emcAcv337ure/7iPB1RoCenh52dnYIhUJomobD4fj0GJvNZn4bqYYaQvl8AGdnZ2xubhIOh9E0\nDQCPx0NnZydQHWsQyufTdZ2hoSEURaGtrY2WlhYeHx9rqn5gjOndbrf52IrX0O/8n/+jLn+1Bmu2\nOXu9XmKxGAAXFxe0trbS1NQEgMPh4ObmxnwhU6kU7e3tpNNpotEo6+vr5ni7WCwyMjJCNpsFjDfd\nx07LSvpNvnA4zOHhIWDsUPxobi6Xi2QyCRgj4b6+vgokKvWbfABXV1e4XC7zPLlcjrGxMV5fXwFI\nJBKWqB98nRFgfHycTCbD8/Mz8Xgcj8fz6TG9vb3m89VQQyifL5fLsbS0RCgUMndmA0xOTpJOp4Hq\nWINQPt/BwQGRSAQwxqaZTAZd12umfmA0psbGRnPEa9Vr6HecTif5fJ67uzsKhQLxeByv1/tna7Cm\n/5UqGAySTCZRFIWFhQUuLy/RNA2fz0c0GmVvb4+6ujrcbjczMzOsrKxwdHSE3W43zxGJRDg9PWVr\nawtVVdF1ncXFRVRVrWAyw0/zPTw8MD09TbFYpFAomD8BuL6+Zn5+nvf3d7q7u81NcZX203wAsViM\n8/PzkrH29vY2+/v7NDQ00NXVxdzcHIqiVCpWia8ynpycsLGxgaIojI6OMjw8XPaYjo4Onp6emJ2d\n5eXlBbvdjt/vNyc/lfTTfLu7u6ytrZXsIQgEAtze3rK8vIyqqthsNvx+P83NzRVMZvhpvnw+z9TU\nFNlslre3NyYmJujv76+Z+oHxYXl1dbXkltnx8bElr6GpVIpAIMD9/T319fXous7AwABOpxOfz0ci\nkSAYDAIwODhojuL/Yg3WdHMWQgghqlHNjrWFEEKIaiXNWQghhLAYac5CCCGExUhzFkIIISxGmrMQ\nQghhMdKchRBCCIuR5iyEEEJYjDRnIYQQwmL+AeEotUIS59s3AAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 721
+ },
+ "outputId": "85652bcd-50f5-4f01-d3bb-53a9b8c433fb"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000)"
+ ],
+ "execution_count": 126,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07239858\n",
+ "Loss after epoch 50 is 0.0723927\n",
+ "Loss after epoch 100 is 0.072386816\n",
+ "Loss after epoch 150 is 0.07238092\n",
+ "Loss after epoch 200 is 0.072375044\n",
+ "Loss after epoch 250 is 0.07236916\n",
+ "Loss after epoch 300 is 0.07236328\n",
+ "Loss after epoch 350 is 0.072357394\n",
+ "Loss after epoch 400 is 0.072351515\n",
+ "Loss after epoch 450 is 0.072345644\n",
+ "Loss after epoch 500 is 0.07233974\n",
+ "Loss after epoch 550 is 0.07233387\n",
+ "Loss after epoch 600 is 0.07232799\n",
+ "Loss after epoch 650 is 0.07232211\n",
+ "Loss after epoch 700 is 0.07231623\n",
+ "Loss after epoch 750 is 0.07231036\n",
+ "Loss after epoch 800 is 0.072304465\n",
+ "Loss after epoch 850 is 0.07229859\n",
+ "Loss after epoch 900 is 0.07229271\n",
+ "Loss after epoch 950 is 0.07228684\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.015346416\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XlYlXX6x/H3WVhEcEEBFTQVFRVl\n08wl1zQnbfs11ViZlrbvTaUNLbaalVpWU1Nmu6VT2YxtVja2au4g4I4bbiyKyAGBszy/P9BjlIoL\n8MDh87qurjye7znctxifnuXcX4thGAYiIiJSa1jNLkBEREQqUjiLiIjUMgpnERGRWkbhLCIiUsso\nnEVERGoZhbOIiEgtYze7gCNycwtN/fpNmwaRn19sag3Vydf7A9/vUf3Vbb7eH/h+j1XdX1hYyHGf\n05HzYXa7zewSqpWv9we+36P6q9t8vT/w/R5rsj+Fs4iISC2jcBYREallFM4iIiK1jMJZRESkllE4\ni4iI1DIKZxERkVpG4SwiIlLL1JohJLXRyy+/wIYN69i/fx8lJSW0ahVJo0aNmTz5+Sp5/8svv4jw\n8Ais1qP/j/TKK2+c8fv+8suPnHNOXw4eLGDWrNeZMOGhM35PERGpOScVzhs3buS2227juuuuY/To\n0RWeW7x4MdOnT8dmszFgwABuv/12ACZPnkxqaioWi4Xk5GTi4uKqvvpqdued9wLw1Vefs2VLJnfc\ncU+Vf42pU18iKCioSt9zzpzZJCWdTbNmzRXMIiJ1UKXhXFxczJNPPkmfPn2O+fxTTz3FrFmziIiI\nYPTo0QwfPpz9+/ezfft25s6dS2ZmJsnJycydO7fKizfLqlUrmDPnA4qLi7njjnu57747+PLL7wF4\n+OEJXHbZlXTu3IXJkx+nsLAQt9vNPfc8QIcOHU/q/UeOPO9P77d69UqKihzs2LGdXbt2ctdd99Gn\nTz8WLPiSTz6Zi8ViYdSoa3A6naxdm87999/Fgw8+wuOPP8ysWe+zdOlSnntuKna7nbCwcP7xj0dZ\nuPAb1qxJ4cCBfHbs2M7VV1/LhRdeWm1/biIicnIqDWd/f39mzpzJzJkz//RcVlYWjRs3pmXLlgAM\nHDiQJUuWsH//foYOHQpAdHQ0BQUFOBwOgoODT7vQxxY/zOeZ/znt1x/LRdGX8ljfp07rtZmZm/no\no3n4+/sf8/l///sjzjmnLxdddClbt25hxoypvPjiq2dSLjk52Uyd+hK//baY//73U+LjE3jnnTd5\n992PKCtz8vTTk5gyZTpvvvkvpk59iYKCA97XTpo0ialTXyYiogXTpz/Ld98twGKxkJm5mX/96y12\n7sxi0qRkhbOIyB843U6+3b6AeFcXouwdauRrVhrOdrsdu/3Yy3JzcwkNDfU+Dg0NJSsri/z8fGJj\nYyv8fm5u7gnDuWnToBPOLQ1q4I/Vaqms3FMS1MC/wuDx4w0hDwkJJCjo6NomTYLo2rULkZHNALBY\nLN7nAgL8aNIkiA0bMti/fz+LFn0LQGnpoT+9v81m5R//uBebrbzvpk2b8tJLLx3z/Ro2DKBPn3MI\nCwshJqYdpaWHKCjIoWPHDkRFhQEwa9ZM7/s2bx6MzebEbrfi5+fGYrHQrVv5kfugQf1Zvnw5Xbt2\n5eyze9CiRRNCQvw4dKjohIPY64K6Xn9l1F/d5uv9gW/16ChzMGvVLKb/Np0dBTsY0XEEX179ZY18\n7Rq5IcwwjErXVLbTx4TER5mQ+GhVleR1ZDessLCQ4+6MVVhYQnFxmff5AweKMQyL97FhGN5fFxUd\n8j5/55330a3b0Wvtf3x/t9vDM8+8UOGac25u4THfr6ioFD+/BuTmFpKfX0RZmYuCghJKSsqO+b55\neQ4KCopwuTzs21dU4T337TtISYmLwsISyso85OYWUlxcjNvtMX13sDNxou+hL1B/dZuv9we+02Nu\ncS6z0v7FW+kzOVB6gAb2BtzQ/WYeH/ZolfZXbbtShYeHk5eX532cnZ1NeHj4n34/JyeHsLCwM/lS\ntZrFYqGkpISSkhI2btwAQNeu3fjppx8A2Lp1C3PmfHBG73csZ53Vlh07tlNcXExpaSn33HMbhmFg\nsVhxu93edY0aNcJisbB3714AUlJW0blzl9PoVETEd20pyOSBH++lx/uxTF/5PDaLjQlnJ7Pq2rVM\n7v88rUJa1VgtZ3TkHBUVhcPhYOfOnbRo0YJFixYxdepU8vPzefnllxk1ahQZGRmEh4ef0fXm2u7S\nSy/nppvG0rZte2JiykPv8sv/xtNPP8Ztt92Ax+PhnnvuP6P3O5YGDRowfvwt3HPPbQD87W9XY7FY\nSExM4rbbxvPQQ4951z755JM8/vhD2Gw2IiOjOO+88/n2269Pr2ERER9yoCSfB368l/mZn2Fg0KZR\nW25LuJNRMdcQ5Fe1n6Y5WRajknPO6enpPPvss+zatQu73U5ERARDhgwhKiqKYcOGsXz5cqZOnQrA\n+eefz/jx4wGYOnUqK1aswGKxMGnSJDp37nzCQsw+FeIrp2OOx9f7A9/vUf3Vbb7eH9TNHgtKD3DF\n/EtIyV1N9+bx3Jl4DxdGX4Ld+udj16ru70SntSsN55pi9je0Lv6lOhW+3h/4fo/qr27z9f6g7vVY\nWHaQKz+/lJXZKxjV+RpeHPxPrJbjX+2tyXDW+E4REal3HGWFjPrir6zMXsEVnUbxwqBXThjMNa32\nVCIiIlIDHE4HV315Ocv3LuWyjlfw0pDXsFmP/1FeMyicRUSk3ihyFjH6yytZumcJl0RfxivnvV7r\nghkUziIiUk8UO4sZ89UoFu/+hQvbX8KrQ2ce88av2kDhLCIiPq/EVcLYr6/i510/MqLdRbw+7C38\nbH5ml3VctfN/GWqJPXt2M2bMKGJiyj8GVlZWxjXXjGXgwMGn/F6ffjqXAwcOMGDAIH766QfGj7/5\nmOuObPfo51f5X5otWzYzffpzf9pmcuDAc+jePd77uFmzZrz66iunXPMfLVq0kMGDh7Jp04YT9iAi\nUls4ygrZU7SHR359kB93LmJ42wt44/y3a3Uwg8K5Um3anOUNv4MHC7j++mvo3bsPAQGBp/V+HTvG\n0LFjzHGfP7Ld48mE8/EEBwdXyb7Qf/TBB+8yePDQSnsQEalJm/I38kPW9+wp2sPeCv/sxeE8+tGn\noW3O583h7+FvO/aGRbWJwvkUNGrUmGbNmrNv3z7efnsmdrsfBw8e4IknpvDcc0+ze/cuXC4XN9xw\nCz16nM2KFct46aVphIY2o1mz5rRqFcmqVSuYN+/fPPXUcyfc7nHGjNeYP/8zFi5cgMVipX//QVx1\n1WhycrJ55JEH8fPzo0OHTidd+86dO7nttjuYNet9AMaPv5annnqWt956g+bNw9iwYR3Z2Xt59NGn\niInpzOzZ7/LDD99jsVi55ZY7WL9+LZs3byQ5+QEuv/xv3h6+//475s6djc1mIyamC/fccz+zZr1+\nzO0tRUSqkmEYvJvxFg//MpEyT1mF55oFNuOsRm1p0bAFLRu2okPTTozrdiMBtgCTqj01dSacGz72\nMAGfV+2WkaUXXUrRYye/ZeSePbs5eLCA8PAIoHxm9cSJD7FgwZc0a9acf/zjUQ4cOMDdd9/Cu+/O\n4fXXX+GRR56kY8dO3H//XbRqFel9r+LiohNu95ibm8MPP3zPq6/OAuDWW8czePBQ5s2by3nnnc+V\nV17FBx+8w+bNG8/4z6GsrIzp01/hP//5hAULviQoKIgffvie119/h927d/HBB+/w4IOPMHv2u0ye\n/DyrVq043EMxb7zxT95++0OCgoKYMOFe73N/3N5S4SwiVclRVsj9P97NvE2f0DSgKVP6TKNT0860\naNiCiIYt6kwIH0+dCWez7NixnTvuuAko39v64Ycf926h2bVr+baY6elrSE1dzZo1KQCUlpbidDrZ\ns2cPHTuWH90mJCRRWlrqfd9t27bSpk1bAgICCQgIZMqU6RW+7rp1GezcmcWdd5Zf1y0uLmLv3t1s\n27aVwYPL98pOTOzJb78t/lPNDofDWzNAdHQHbrvt+NeH4+MTAQgLi2Dt2gw2btxA167dsFqtREW1\n5sEHHznm67KydhAV1ca7q1ZiYg82blwPQFxcAlC+OYrD4Tju1xYROVVr92Uw/ptryTywmZ4RvZh5\n/jtEhkSZXVaVqjPhXPTYU6d0lFtVfn/N+Y/sdj/vv8eMGcewYX+p8LzVevRm+D9OSbVabRiG57hf\n1273o0+ffkyY8FCF3589+10sh6fYHO/1x7rmXFZ2sMJjl8vl/fWR/aSP1GmzWfF4Kp/qarFU7Mvl\nchIQEHDM9xQROVOGYfDR+g948Kf7KHGXcGv8nTzc+7Faf3PX6dBHqapA167d+OWXHwHIz9/P66//\nE4DmzcPYsWMbhmGwevXKCq+pbLvHmJgurFq1kpKSEgzD4MUXp1JaWkKbNmexfv1aAO8p5JMRHBxM\nfv5+DMNg3748du/eedy1MTFdSEtLxeVysX//Pv7xj/Idtf4Y2K1bn8XOnTsoLi4CYPXqVcTEdD3p\nmkRETlaRs4i7/ncr9yy6nQB7IO9e8BGP93vaJ4MZ6tCRc202ZMhQVq1azi23jMPtdjNuXPkp5Ztu\nuo2HH55IixYtvdepj6hsu8eXX36DK6+8ittvvxGr1cqAAYMICAjkiiuu4pFHHuSnnxYRHd3xpGts\n3LgxPXv24oYbxtChQ8cT3m3dsmUrhg8fwR133IRhGNx88+0AdOoUw403juHWW+/y9nD77Xdz3313\nYrFYiYtLID4+gRUrlp7Sn5+IyIls3L+B8d9cy4b89SSGJ/HG+e9wVqO2ZpdVrbQr1WF1bTeVU+Xr\n/YHv96j+6jZf7w+qvseDpQW8tOoF3ljzKiXuEm7ofjOT+j5l2s1eNbkrlY6cRUSkVnG6nby39m2m\nLn+GfSX7aNmwFU+f+xwXRl9sdmk1RuEsIiK1gmEYfL31S5787VEyD2ymoV8wyec8yk1xtxHkF2R2\neTVK4SwiIqZbmb2cxxY/zNI9S7BZbFwXO577z/4H4UHhZpdmCoWziIiYIr9kP0t2L+azTZ/w38x5\nAPyl7Qge6fMEHZue/AREX6RwFhGRGrG/ZB9Ldi9m8a6f+XX3L6zbl4FB+T3JCWGJPNb3afpGnmty\nlbWDwllERKrNquwVfLrx3/y6+xfW7kv3/n6gLZBzIwfQN/Jc+rXqT6+WvbFaNHrjCIWziIhUuVXZ\nK5i6fAoLd3wLlIdx/8iB3jBOjOhR5+dfVyeFs4iIVJnV2SuZumIK323/BoA+rfpxd9J99IvsrzA+\nBQpnERE5Yyk5q3hp4VS+2PgFUB7KE85Opl9kf5Mrq5sUziIictrS89KYsvRJvt2+AIDeLfsyoVcy\n/Vr1x2KxmFxd3aVwFhGR0/Jj1iKu/epvlLhLOKdlHyYPe4puDXsqlKuAwllERE7ZD1n/Y8xXozAw\neGv4B4xsfxHh4Y18fn54TVE4i4jIKVm043vGfn0VBgbvXvARQ9oMNbskn6NwFhGRk7Zox/eM+XoU\ngIK5GukT3yIiclIUzDVH4SwiIpX6346F3mB+74I5CuZqpnAWEZET+t+O7xj79VVYsPDeBXMY3OY8\ns0vyebrmLCIix1UezFeXB/OIOQxqPcTskuoFhbOISD22t2gP2w9uZ5cji52FO9nlyGK3Y5f31wdK\nDxBoC1Qw1zCFs4hIPXTIdYiJP/2dOetnH/P5hn7BRAVH0TOiF3ck3qOtHGuYwllEpJ7JKtzB9QtG\nsyY3hdhm3RnSZiiRIVFEBUcRGdyaqJAoGvk31qQvEymcRUTqkR+zFnHzd9ezv2Q/o7uMZXL/5wm0\nB5pdlvyBwllEpB4wDINXUmbw9G+PYbPYmDpwBmNirze7LDkOhbOIiI9zOB3c87/bmZ/5GS0btmLW\n8Pfo2aKX2WXJCSicRUR82JYDmxn79dVsyF9P75Z9eXP4e4QHhZtdllRCQ0hERHxQqbuUOetnM+yT\nQWzIX8+N3W/h04s/VzDXETpyFhHxITsLs3gv420+WPcueYdyaWBvwD/Pe4MrYkaZXZqcAoWziEgd\nZxgGP+5cxFvpM/l229d4DA9NAppwa/ydjOt+I2c1amt2iXKKFM4iInVUQekB5q7/kLcz3iTzwGYA\n4sISGNftRi7t8FeC/IJMrlBOl8JZRKQOOVCSzzfbvubLLfNZlPU9pe5S/K3+XNFpFOO630hSeE8N\nD/EBCmcRkVpu36F9fL31C77Y8l9+2vkDLo8LgM6hXbi809+4ussYmjdobnKVUpVOKpwnT55Mamoq\nFouF5ORk4uLivM8tXLiQ1157DX9/f0aOHMno0aNZunQpd999Nx07dgSgU6dOPPLII9XTgYiID3I4\nHXyyYS6fZ/6Hxbt/wW24gfLT1he2v5gL219Ch6YdTa5Sqkul4bxs2TK2b9/O3LlzyczMJDk5mblz\n5wLg8Xh48skn+eyzz2jSpAk33ngjQ4eWb8Ddq1cvXnrppeqtXkTExxwoyefNtNeZueY18kvzAegR\ncTYXtr+Eke0vom3jdiZXKDWh0nBesmSJN3Cjo6MpKCjA4XAQHBxMfn4+jRo1IjQ0FIDevXuzePFi\nIiMjq7dqEREfk1Ocw+up/+Tt9DdxOAtpGtCUCWcnc3WXa2kVrJ+p9U2l4ZyXl0dsbKz3cWhoKLm5\nuQQHBxMaGkpRURHbtm0jMjKSpUuX0qtXLyIjI9m8eTO33HILBQUF3HHHHfTr169aGxERqYt2Fe7k\nnykz+GDtu5S4SwgPiuD+sx9kTOz1BPsFm12emOSUbwgzDMP7a4vFwpQpU0hOTiYkJISoqCgA2rZt\nyx133MEFF1xAVlYWY8aM4dtvv8Xf3/+479u0aRB2u+00Wqg6YWEhpn796ubr/YHv96j+6rbf97d5\n/2ae/eVZ3k19F6fHSZvGbZjYbyLjEsfV6V2i6tP3sDpVGs7h4eHk5eV5H+fk5BAWFuZ93KtXLz78\n8EMApk2bRmRkJBEREYwYMQKANm3a0Lx5c7Kzs2nduvVxv05+fvFpN1EVwsJCyM0tNLWG6uTr/YHv\n96j+6rYj/W3Yv54XV07ls82f4DE8tG8czd1J93F5p7/hZ/OjMN9JIU6zyz0t9eV7WJXvdzyVztbu\n168f33zzDQAZGRmEh4cTHHz0VMsNN9zAvn37KC4uZtGiRfTp04f58+cza9YsAHJzc9m3bx8RERFn\n2oeISJ21es9qxi24lgFzzuHTTf8mpmkXXh/2Fr9etYKruozGz+ZndolSi1R65JyUlERsbCyjRo3C\nYrEwadIk5s2bR0hICMOGDePKK69k3LhxWCwWbrrpJkJDQxkyZAj3338/33//PU6nk8cee+yEp7RF\nRHzVir3LeHHlVL7dvgCAhLBE7u05geFtL8Bq0d5DcmwW4/cXkU1k9qkQnY6p+3y9R/VX+xiGQbGr\nGIfTgaPsII4yB4XOQgrLCikoPcAnG//NTzsXAdCvdT/ujL+Pwa3P89kJXnXxe3gqavK0tiaEiYic\nokU7vmfCT/eSVbgDj+E54doBUYP5e48HuDj+L+TlOWqoQqnrFM4iIifJ5XHx7LKnmbFqGn5WP3pE\nnE2Ifwghfo0I8Q+hoX8wIX4hBPuHEOIfQvfmcSSEJwH47NGyVA+Fs4jISdjt2MXN341j6Z4lnNWo\nLTPPf8cbvCJVTeEsIlKJhdu/4Y7vb2Z/yX4uir6UFwa9TKOAxmaXJT5M4SwichxOt5PJS5/gnykz\nCLAF8OyA6VwXO16nqKXaKZxFRI5hZ2EWN317PSuyl9G+cTQzh79L9+Zxlb9QpAoonEVEAI/hYVP+\nRlZlr2Bl9grmZ87jQOkBLut4OVMHziDY37fHUkrtonAWkXopuzibVdkryv/JWUlKzioKyw56n2/o\nF8y0QS8xustYncaWGqdwFpF6pcxdxm0Lb2R+5mcVfr9jk06MaHchiRE96BHek67NummkpphG4Swi\n9UaZu4wbvh3Lgq1fEh+WyAXtRpIU0ZPE8CQaBzQxuzwRL4WziNQLTreTG7+9jgVbv2RA1GDeHzGH\nBvYGZpclckyaui4iPs/pdnLTd9fz9dYv6B85kPcu+EjBLLWawllEfJrT7eTm78bx5Zb5nBs5gPdH\nzCXIL8jsskROSOEsIj7L5XFx68Ib+GLLf+nb6lwFs9QZCmcR8Ukuj4vbFt7A/MzP6N2yL7NHfkxD\nv4ZmlyVyUhTOIuJzXB4Xty+8kf9snsc5Lfvw4YWfKJilTlE4i4hPSc9LY/w3Y/hs86ec3eIcPhr5\nCcF+wWaXJXJK9FEqEanzDpYWMG/TJ8xe9x6puasBOLvFOcy58FON3ZQ6SeEsInWSYRgs3bOE2eve\nY37mZxxyHcJmsTG87QVc02UsQ886H7tVP+KkbtLfXBGpU0rdpcxKe4P3175N5oHNALRt1I5ruozh\nb52vpkXDliZXKHLmFM4iUmfkFOdw/YJrWL53KQG2AP7a8UpGdx1Ln1b9sFp0C434DoWziNQJ6Xlp\njPlqFDsdWVzW8XKm9J9Gk8CmZpclUi0UziJS63255XNuX3gjxa5iks95lLuT7tM2juLTFM4iUmsZ\nhsELK59nyrKnCLI35J2/fMiI9heaXZZItVM4i0itdMh1iHv+dxufbf6UqODWvDdiDt2adze7LJEa\noXAWkVpnj2M3Y7++ipTc1ZzTsg9vDf+AsKAws8sSqTEKZxGpMTnFOTy++GHS89YQYAsg0N7g8L8D\nadwwBFw2AmyBfLvta7KL93JV59E8N/AFAmwBZpcuUqMUziJS7QzD4NNN/+ahnyeQX5pPQ79gPIab\nElcJBsaf1lstVp7oN5mb427XjV9SLymcRaRaZRft5YEf72HBtq8IsgfxTP/nub7bjVgtVgzDwOlx\nUuI6RHATP3bl5FHqKiUkoBERQRFmly5iGoWziFQLwzD494aPePjXBykoPUC/Vv15YfArtG3czrvG\nYrHgb/PH3+ZPWHAI1kPaa1kEFM4iUg32OHZz3w93sXDHtzT0C+bZAdMZGztOU7xETpLCWUSqjGEY\nzFk/m0d+/QcHywoYEDWY6YNeok2js8wuTaROUTiLSJXIL9nP33+4iy+3zCfYL4Rpg15idJexuqFL\n5DQonEXkjP22ezG3LryBXY6d9G7Zl1eHziQqpLXZZYnUWQpnETltLo+L6SueY/rK5wCYcHYy9/Z4\nAJvVZnJlInWbwllETsvOwixuXXgDS/csISq4Na8Oe5PeLfuYXZaIT1A4i8gp+zzzP/z9h7soKD3A\nxdH/x9SBL2r7RpEqpHAWkZNiGAbbDm7lldUv8v7ad2hgb8D0QS9zTZcxuulLpIopnEXkuPYW7eHn\nnT/yy66f+Hnnj+x0ZAEQ26w7rw97i06hMSZXKOKbFM4i4uUoK+SHrEX8sutHft75I5sObPQ+1zSg\nKRe2v4QBUYMY1fkaAu2BJlYq4tsUziL1nGEYLN+7jNnr3uW/m+dR7CoGIMjekPPaDOPcyIEMiBpI\nbPPumvAlUkMUziL1VN6hPD7eMIfZ695lY/4GANo0assVnf7GoNbnkRiehL/N3+QqReonhbNIPeL2\nuPlx5yJmr3uPBVu/xOlx4m/15/86/JVruo7l3MgBOjoWqQUUziL1xK+7fub+H+8m88BmALqEdmV0\n17H8tdOVhAY2M7k6Efk9hbOIjztYWsATSybx3tq3sFqsXN35WsbEXk9ieA99BEqkljqpcJ48eTKp\nqalYLBaSk5OJi4vzPrdw4UJee+01/P39GTlyJKNHj670NSJSM77btoD7f7yHPUW76RLalRcGv0JS\nRE+zyxKRSlQazsuWLWP79u3MnTuXzMxMkpOTmTt3LgAej4cnn3ySzz77jCZNmnDjjTcydOhQduzY\ncdzXiEj1yzuUx8O/TGTepo/xs/ox4exk7kr6u27wEqkjKg3nJUuWMHToUACio6MpKCjA4XAQHBxM\nfn4+jRo1IjQ0FIDevXuzePFisrKyjvsaEak+hmHwn82fkvzzA+wr2UdSeA9eGPxPujTranZpInIK\nKr0tMy8vj6ZNj87MDQ0NJTc31/vroqIitm3bhtPpZOnSpeTl5Z3wNSJS9QzDYNmepVz71d+4+btx\nFLuKeaLfZL68bKGCWaQOOuUbwgzD8P7aYrEwZcoUkpOTCQkJISoqqtLXHE/TpkHY7eZuMxcWFmLq\n169uvt4f+H6Pf+wvpyiH91Pf583Vb7I+bz0Ag9sOZuZFM4kOjTajxDNS375/vsjXe6yp/ioN5/Dw\ncPLy8ryPc3JyCAsL8z7u1asXH374IQDTpk0jMjKS0tLSE77mWPLzi0+5+KoUFhZCbm6hqTVUJ1/v\nD3y/xyP9lX9W+X98sPY9vtn2VYXPKl/dZQwDogZhcVvq3J9Fffn++TJf77Gq+ztR0Fd6Wrtfv358\n8803AGRkZBAeHl7h2vENN9zAvn37KC4uZtGiRfTp06fS14jIqdt2YBvPLnuanh90Z9QXf+WLLf+l\nQ5NOPH3us6y5bgOvn/82A1sP1sejRHxApUfOSUlJxMbGMmrUKCwWC5MmTWLevHmEhIQwbNgwrrzy\nSsaNG4fFYuGmm24iNDSU0NDQP71GRE7dIdchvtryOR+u/4Cfd/4AQLBfCNd2vZ7RXcaQEJ6kMBbx\nQRbjZC4I1wCzT4XodEzd5ys9GobBmtwUZq97j3mbPuFgWQEA/dv05/Loq7i4w//R0K+hyVVWPV/5\n/h2Pr/cHvt9jTZ7W1oQwkVoiv2Q/H2+Yw4frP2DtvnQAIoJacH23GxjV+Wp6d0zy6R98InKUwlnE\nZDnFObya8hLvpM+i2FWEn9WPC9tfwtVdRjOo9XnYrfrPVKS+0X/1IibZ49jNP1Nm8F7G25S4S2jZ\nsBUTeiVzZcxVNG/Q3OzyRMRECmeRGrazMIuXVk3nw3XvU+YpIyq4NXcl/Z2ruowmwBZgdnkiUgso\nnEVqyLaCrby0ajpzN3yI0+PkrEZtuSfpfq6IGaWZ1yJSgcJZpJrtO7SPaSum8E7GLFweF9FNOnBv\njwe4rOMVup4sIseknwwi1aTEVcLMtH/x4sqpFJYdpF3j9kzs9RCXRF+GzWruqFoRqd0UziJVzGN4\n+GzTJzz92+PsdGTRNKApT5/0tYijAAAgAElEQVT7LGNjx+v0tYicFIWzSBVavOsXHlv8ECm5q/G3\n+nN7wt3c0+M+Ggc0Mbs0EalDFM4iVWBnYRbJPz/Agm1fAXBZx8tJPmcSbRqdZXJlIlIXKZxFztCC\nrV9x1/9u4UDpAXq37MtjfZ8iKaKn2WWJSB2mcBY5TWXuMp78bRKvp/6TQFsgzw98kTFdr9dGFCJy\nxhTOIqdhW8FWbv7uelbnrKJjk068cf47xDbvZnZZIuIjFM4ip+jzzP9wz6I7KCw7yJUxVzFlwDSC\n/bRfuYhUHYWzyEkqcZUwaXEyb6e/SZA9iJeGvMaozteYXZaI+CCFs0glDMNgdc5K7v/xHtLz1tAl\nNJaZ579Dp9AYs0sTER+lcBY5jswDm/h048fM2/QxWwoyAbi26/U8de4UGtgbmFydiPgyhbPI7+xx\n7OY/m+cxb9PHpOauBqCBvQH/1+GvXNXlWga1HmJyhSJSHyicpd5zup3M2/Qxczd8yK+7fsbAwGax\nMbTN+VzW6Qr+0m6kbvgSkRqlcJZ6y+l2MnfDh7y4aho7Dm4D4JyWfbis4xVcFH0pzRs0N7dAEam3\nFM5S75S5y5izfjYzVk0jq3AHAbYAxne/iVvj79S4TRGpFRTOUm+Uukv5aN0HvLRqOjsdWQTaArmx\n+y3cmXQvLRq2NLs8EREvhbP4LMMwyC/dz5YDmazKXsFrqa+wy7GTQFsgN8fdxh2J9xDRsIXZZYqI\n/InCWeo8t8fNmtwUcvbsJCUrna0FW9hakMmWgi0UlB7wrmtgb8At8Xdwe+LdRARFmFixiMiJKZyl\nTttbtIebvxvHkt2/Vvh9f6s/bRu3o3fLPrRrHE10kw5c0O5CwoPCTapUROTkKZylzvoxaxG3LhxP\n3qE8hp01nP+LvYTmtla0bxxNZHAUNqvN7BJFRE6LwlnqHLfHzbQVzzJtxbPYrXaePvdZbuh+C+Hh\njcjNLTS7PBGRM6ZwljolpziHWxfewM87f6B1SBtmnv8OSRE9zS5LRKRKKZylzli86xdu/m4c2cV7\nGd72Al4a8hpNA0PNLktEpMopnKXW8xgeXl71As8sexILFib1eYrbEu7EYrGYXZqISLVQOEutlpGX\nziO/Psgvu36iZcNWvHH+O5zTsrfZZYmIVCuFs9RK2cXZPLv0KT5c/z4ew8P5Z/2FF4e8qnnXIlIv\nKJylVjnkOsTrqf9kxqrpFDkdxDTtzOP9nmZIm2FmlyYiUmMUzlIrGIbBZ5s/4aklj7HTkUWzwGY8\n2ucJru16HXar/pqKSP2in3piuhV7l/HIrw+yMnsF/lZ/7ki8h3uS7qNRQGOzSxMRMYXCWUw1f/Nn\n3PTd9XgMD5dEX8bDfR7jrEZtzS5LRMRUCmcxzYKtX3HLwvEE2Rvy7gUf0j9qoNkliYjUCgpnMcX/\ndizkhm/G4G/158MLP6F3yz5mlyQiUmtYzS5A6p9fd/3MdV9fjdVi5f0RcxXMIiJ/oCNnqVHL9izl\nmi+vxG24eX/EHJ3KFhE5BoWz1JiUnFVc9eVfKXWXMGv4+/rssojIcSicpUak56Vx5eeXUuR08K+h\nsxjR/kKzSxIRqbUUzlLtNuxfz5WfX0JBaQEvDXmNSzv+1eySRERqNYWznLZiZzHPLZ/Md9sWYLPa\n8LP642e142fzx9/qj91qx9/mz8rsFeQdymPqwBn8rfPVZpctIlLrKZzltPy2ezF3L7qNrQVbaOgX\njL/VjzKPE5fHSZm7DAPDu9ZutTP53OcYE3u9iRWLiNQdJxXOkydPJjU1FYvFQnJyMnFxcd7nZs+e\nzfz587FarXTr1o2HHnqIefPmMWPGDNq0aQNA3759ufXWW6unA6lRRc4inln6BDPX/AuAW+PvZGKv\nhwjyC6qwzu1xU+Ypw+VxYrXYaOjX0IxyRUTqpErDedmyZWzfvp25c+eSmZlJcnIyc+fOBcDhcDBr\n1iy+/fZb7HY748aNIyUlBYARI0YwceLE6q1eatSS3b9y9/9uY9vBrXRo0pEXB79Kr5bnHHOtzWqj\ngbUB0KBmixQR8QGVhvOSJUsYOnQoANHR0RQUFOBwOAgODsbPzw8/Pz+Ki4sJCgri0KFDNG6szQp8\njcPp4OnfHmNW2htYLVZuT7ibCb2SaWBX8IqIVIdKJ4Tl5eXRtGlT7+PQ0FByc3MBCAgI4Pbbb2fo\n0KEMHjyY+Ph42rVrB5QfcY8fP56xY8eydu3aaipfqpPD6eCrLV8waG5fZqW9QaemMXx52XdM6vuk\ngllEpBqd8g1hhnH0Rh+Hw8Hrr7/OggULCA4OZuzYsaxfv574+HhCQ0MZNGgQq1evZuLEiXz++ecn\nfN+mTYOw222n3kEVCgsLMfXrV7fK+it2FrM4azGLti5i0bZFLN+9HJfHhdVi5cF+DzJp0CQC7YE1\nVO3pqe/fw7pO/dV9vt5jTfVXaTiHh4eTl5fnfZyTk0NYWBgAmZmZtG7dmtDQUAB69uxJeno6l19+\nOdHR0QAkJiayf/9+3G43Ntvxwzc/v/iMGjlTYWEh5OYWmlpDdTpWf4ZhsHTvb/yQ9T2/7vqZVdkr\ncHqcANgsNhLCE+nbqj+Xdvwr3ZvHUZjvpBCnGeWflPr4PfQl6q/u8/Ueq7q/EwV9peHcr18/Xn75\nZUaNGkVGRgbh4eEEBwcDEBkZSWZmJiUlJQQGBpKens7AgQOZOXMmLVu25MILL2Tjxo2EhoaeMJil\n5u1x7GbiT39nwbavALBarMQ1j6df5ADOjexPr5a9CfFvZHKVIiL1U6XhnJSURGxsLKNGjcJisTBp\n0iTmzZtHSEgIw4YNY/z48YwZMwabzUZiYiI9e/YkKiqKBx54gDlz5uByuXj66adrohc5CR7Dw/tr\n3+GJJY9SWHaQfq36c2vCHfRu2ZdGAbqZT0SkNrAYv7+IbCKzT4XUh9Mxv21axd9/uIslu3+lkX9j\nHuv7FNd0GYPFYjG7vCpRH76H6q/u8vX+wPd7rFWntaXuc7qdPPPzMzz+4+OUuksZ0e4ipgyYSouG\nLc0uTUREjkHh7ONSc1Zz7w93kp63hvCgCJ7pP5WLoi8xuywRETkBhbOP2l+yj6nLp/BW+kw8hofx\nieOZmPgoTQKbVv5iERExlcLZx5S5y5iV9gbTVz5HQekB2jeO5vmBL3JZ4oU+fS1IRMSXKJx9hGEY\nfLnlc55Y8gjbDm6lSUATnuo3heu63YC/zd/s8kRE5BQonH1Aas5qHl2czJLdv2K32rkp7lbu6zmR\npoGhZpcmIiKnQeFch+127GLy0if494aPAPhL2xFM6vsk0U06mlyZiIicCYVzHbT94DZeXvUic9Z/\nQJmnjNhm3Xmi32T6Rw00uzQREakCCuc6ZFP+RmasmsanG/+N23DTrnF77u3xAFd0GoXNqvGoIiK+\nQuFcB2TkpfPiyqnMz/wMA4POoV24O+k+LulwGXarvoUiIr5GP9lrKcMwWL53Ga+sfsG7OUVcWAL3\n9niAC9qNxGqpdCtuERGpoxTOtYhhGKzKWcH8zf/hiy3/JatwBwBntziHv/d4gCFthvnMHGwRETk+\nhbPJPIaHldnLmZ/5H77I/C+7HDsBCPYL4a8dr+SarmPo16q/QllEpB5ROJtkx8HtzFzzGp9n/pfd\nRbsAaOTfmCtjruKi6EsZ1HoIAbYAk6sUEREzKJxrWHbRXl5Y+Tzvr30Hp8dJ44AmjOp8DRdHX0r/\nqEEKZBERUTjXlPyS/byyegZvpv2LQ65DtG3Ujgm9krk4+v80XlNERCpQOFczh9PBG6mv8s+Ulygs\nO0jLhq14st8Uruo8Gj+bn9nliYhILaRwriaFZQf5aN0HvLhqKnmH8ggNDOXxvpO5rtt4GtgbmF2e\niIjUYgrnKuD2uNmYv4GV2cu9/2zYvx4Dg2C/ECacnczN8bcR4t/I7FJFRKQOUDifhuyivazOWcWq\n7BWszF7OqpyVFDkd3ueD7A3p2+pc+kaey/juNxEa2MzEakVEpK5ROFfiQEk+KbmrSclZxeqcVaTk\nrGJP0e4Kazo1jaFHxNnef2JCO2uspoiInDYlyDFkFe5g6vIp/LZnMVsLtlR4Ljwogr+0HUFCeBKJ\n4T1IiuhB44AmJlUqIiK+SOH8O26Pm7fS3+Dp356g2FVE44AmDIgaTGJ40uEwTqJlw1aa1iUiItVK\n4XxYRk4GYz+7npXZy2ka0JRnB0zjiphR2mBCRKQes2Rn45eWgj09DYafB10Sa+Tr1vtwLnWXMmPl\nNGasmobT4+TSDpfx1LnPER4UbnZpIiJSUwwD657d2NekYk9djT0tFfuaVGx79xxdk54Cb35QI+XU\n63Bevncpf190Jxvy1xMZEsmU/tMZ3vYCs8sSEZHqZBhYs3aUB/GaFPzWpGBfk4o1L7fCMnfLVpQO\nvwBXXAKuuAQaXzoCDhk1UmK9DOfs4mxmrJzKrLQ3MDC4LnY8My6aTulBXUsWEfEphoF121ZvANtT\nU7CnpWDNz6+wzN26DaUjL8YVF48rLh5n9wSM8D+cQQ0OhkOFNVJ2vQnnfYf28cWW//LfzfNYvPsX\nPIaHDk06Mn3wK/Ru2YdGASHkUjN/6CIiUg08HmyZm7EfCeI1KdjT1mA9WFBhmatde8oGDMbVPR5X\nfAKu7nEYobVrHoVPh/OBkny+3vol/9n8KT/t/AG34QagZ0QvLut4OaO7XkegPdDkKkVE5JS5XNg2\nbTwcxCn4rUnFlp6GtejoQCjDYsEd3YGyoeeXn5qOT8DVrTtG49r/8VefDOfV2SuZtuJZFmV9j9Pj\nBCAhLJFLOvyVSzr8H1EhrU2uUERETprTiW3D+sOnplPKT02vTcdy6JB3iWG14u4UQ1lcQvlp6bhE\n3N26YQSHmFj46fPJcH59zat8u30Bsc26c2mHy7i4w//RrnF7s8sSEZHKlJZiX7+2PIDXpGJfsxr7\nurVYSku9Swy7HXdMF5xx8Ydv1orH1bUbNGxoYuFVyyfDeerAF3mo9yRah7QxuxQRETmeQ4ewZ6SV\nh3Da4Zu11q/F4nJ5lxj+/ri6xB4N4bh4XF1iIdC3L0n6ZDgH+4cQ7F83T2WIiPgkhwN7elr5QI/U\nFOxpqdg2bsDidnuXGIGBuOITD4dwAs64BNwxncHf38TCzeGT4SwiIuaxHCzAnramwkAP2+ZNWIyj\nnxE2ghri6tmr/NR093hc8Ym4O3YCu2IJFM4iInIGLPn7y4M4NQU2ZtB02XLsWytuGOQJDsHZp9/R\nU9PxibjbR4PNZlLVtZ/CWUREToolLw/7mtX4rUn1fo7YtmN7hTXWJk3KP0N8ZJhHXAKetu3Aqn0K\nToXCWURE/sS6d0/FYR5rUrHt3lVhjad5c8qGDMXVvTyEGw85l31BoaCd+86YwllEpD4zDKy7dh79\n2NLho2JbTnaFZe6IFpQOG+6dM+2KT8DTslXFIA4LgVxNWqwKCmcRkfrCMLBu34Y9LRW/1MMDPdJS\nse7bV2GZOzKK0r+MPPrRpfhEPBEtTCq6flI4i4j4Io8H27YtvxvmcXjnpYIDFZa525xFaZ9zccYn\nlN813T0eIyzMpKLlCIWziEhd53Zj27zpzxs+OCqeYna1j6ZsyHm4uh8d6GE0aWpS0XIiCmcRkbrE\n5cK2YX35RK01KeWnpzPSsBQXe5cYFgvujp28c6Zd8YnlGz6ENDKxcDkVCmcRkdqqtBT7hnUV9iG2\nr83AUlLiXWLYbLg7dcYVn3B4oEf5zku+NGe6PlI4i4jUBiUl2NemV7g+bF+XgcXp9C4x/Pxwde7q\nHW/p3fChQQMTC5fqoHAWEalpRUXYM9Kxpx0+Lb0mFduGdRXnTAcE4OrWHVdc4tG7pjt3hYAAEwuX\nmqJwFhGpRpbCg9jT02DLekJ+/a18zvSmjVg8Hu8aIygIV1JP70QtV1wC7k4x4OdnYuVippMK58mT\nJ5OamorFYiE5OZm4uDjvc7Nnz2b+/PlYrVa6devGQw89hNPp5MEHH2T37t3YbDaeeeYZWrduXW1N\niIjUBpaCA94hHt6BHpmbvc8HAp6GwTjP6VN+JHxkw4cOHTVnWiqoNJyXLVvG9u3bmTt3LpmZmSQn\nJzN37lwAHA4Hs2bN4ttvv8VutzNu3DhSUlLYunUrjRo1Ytq0afzyyy9MmzaNF198sdqbERGpKZb9\n+7zXh48M9LBt31ZhjadRY8rOHYArLoGgc3uzv10M7nbRmjMtlao0nJcsWcLQoUMBiI6OpqCgAIfD\nQXBwMH5+fvj5+VFcXExQUBCHDh2icePGLFmyhEsvvRSAvn37kpycXL1diIhUI0tODn6/G21pX5OC\nbWdWhTWe0FDKBg7GFZ/o3QbR07add7xlUFgIbo22lJNUaTjn5eURGxvrfRwaGkpubi7BwcEEBARw\n++23M3ToUAICAhg5ciTt2rUjLy+P0NBQAKxWKxaLhbKyMvxPsGF206ZB2O3mntYJCwsx9etXN1/v\nD3y/R/VXzQwDdu+GlSth1aqj/969u+K6iAi44ALo0QOSkqBHD6ytW+NvsXD8n3K1oL8a4Os91lR/\np3xDmPG7zbIdDgevv/46CxYsIDg4mLFjx7J+/foTvuZ48vOLK11TncLCQsj14f+r9fX+wPd7VH9V\nzDCwZu0oPxL+3V3T1rzcCsvcrSJx/WXE4evD5TdreSJa/HnnpTzHCb+cr3//wPd7rOr+ThT0lYZz\neHg4eXl53sc5OTmEHZ67mpmZSevWrb1HyT179iQ9PZ3w8HByc3Pp3LkzTqcTwzBOeNQsIlKtDAPr\n1i34paVWGOhhzc+vsMzdug2lIy8+uhdx9wSM8HCTipb6rNJw7tevHy+//DKjRo0iIyOD8PBwgoOD\nAYiMjCQzM5OSkhICAwNJT09n4MCBBAQEsGDBAvr378+iRYs455xzqr0RERGgfMOHLZnYU1dXnDN9\nsKDCMvdZbSnpP+joMI+4eIzQZiYVLVJRpeGclJREbGwso0aNwmKxMGnSJObNm0dISAjDhg1j/Pjx\njBkzBpvNRmJiIj179sTtdrN48WKuuuoq/P39mTJlSk30IiL1jcuFbdNG79aHfqkp2NLTsBYdPcVs\nWCy4oztQNvT8o0HcPQ6jcRMTCxc5MYtxMheEa4DZ1yl0raTu8/Ue631/Tie29esOn5pOKT81vTYd\ny6FD3iWG1Yq7U4w3hJ1xibi7dcMINv8mJV///oHv91irrjmLiNS4khLs69f+ecOHsjLvEsNuxx3T\npfxjS0eOiGO7Q1CQiYWLVA2Fs4iY69Ah7BlpsHUDwb/+Vh7I69dicbm8Swx/f1xdYo9u+NA9rnzD\nh8BAEwsXqT4KZxGpOQ4H9oz03w30SMG2cYN3w4cGgBEYeDSE4w9v+hDTBfSJD6lHFM4iUi0sBwuw\np6353RaIKdg2b8Lyu9tcjKCGuHqcjTM+gaB+vdnfrjPujp3Arh9NUr/pvwAROWOW/P0VRlva16Rg\n37qlwhpPSCOcfc8tH+YRd3jDh/bR3g0fNN5S5CiFs4icEktuboWJWva0VGw7tldY42nShLL+gw5P\n1CrfBtHTtp02fBA5SQpnETku6949Rz+2lFZ+57RtT8U5055mzSgbfB7O+ETvUbGnzVl/Hm8pIidN\n4Swi5eMtd+2suA/xmlRsOdkVlrkjWlA6bPjhjy4l4IpPwNOylYJYpIopnEXqG8PAun2bd6LWkela\n1n37KixzR0ZResGF3tGW3g0fRKTaKZxFfJnHg21r5h9u1krFWnCgwjJ3m7aU9u3v3YfYFZeA0by5\nSUWLiMJZxFe43dgyN/95wwdHxTugXe3aUzZ4CK64xKMbPjRpalLRInIsCmeRusjlwrZxg/djS35r\nUrGnp2EpLvIuMSwW3B07Uebddal8spYR0sjEwkXkZCicRWq7sjLs69f+brzl4TnTJSXeJYbNhrtT\n5/KPLcUn4OqegCu2Gxze3lVE6haFs0htcugQ9nUZFa4P29dlYHE6gcPjLf38cHXuevRoOC6+fM50\ngwbm1i4iVUbhLGKWoiLsGekVBnrYNqzzzpkGMAICcHXrjqt7Ag3O7U1+2064usRCQICJhYtIdVM4\ni9QAi6MQe3pahZu1bJs2YvF4vGuMBg1wJSThik/wDvRwx3QGPz8AGoSF4NJ4S5F6QeEsUsUsBQeO\nfnQprXy6lm1LZoUNHzwNg3H26l0+3vLwR5fcHTt550yLSP2mcBY5A5Z9+7xDPI4M9LBt31ZhjadR\nY5z9+peHcHz5VC13u2jNmRaR41I4i5wkS3Y2fmmHb9I6PGvatjOrwhpP06aUDRyMKy7h8F3T8eUb\nPmi8pYicAoWzyB8ZBtY9uytuf7gmFdvePRWWeZqHUXresMOnpsvvmvZEtVYQi8gZUzhL/WYYWHdm\nHT4SPnrXtDUvt8Iyd8tWlA6/oOKGDxEtFMQiUi0UzlJ/GAbWrVvwS0v93anpFKz5+RWWuVu3oXTk\nxd7Rls7uCRjh4SYVLSL1kcJZfJPHUz5n+sggjyNzpg8WVFjmbtuOkgGDvfsQu+LiMUKbmVS0iEg5\nhbPUfS4Xts2b4Ov1NPz1N/xSU7Clp2EtcniXGBYL7ugOlA0ddnTDh+5xGI2bmFi4iMixKZylbnE6\nsW1Yj9/vbtSyZ6RhOXQIgCDAsFpxd4qh7MhHl+IScHXrjhEcYm7tIiInSeEstVdp6e/mTKdiX7Ma\n+7q1WEpLvUsMux13TBeccfE06Neb/HYxuGK7Q1CQiYWLiJwZhbPUDocOYc9Iq7jhw/q1WFwu7xLD\n3x9Xl9ijmz3EJ+Dq3BUCAwGNtxQR36FwlprncGBPTysf6HFkmMfGDRU3fAgMPHpK+kgYx3QBf38T\nCxcRqRkKZ6lWloMFhzd8SPEO9LBt3lRhzrQRFISrx9neiVquuATcnWLArr+eIlI/6aefVBlL/v4/\nbfhg37qlwhpPSCOcffodPRqOS8Ad3UEbPoiI/I7CWU6LJS8P+5rV+Hlv1krBtmN7hTWeJk0o6z/I\ne33YGZdQPmdaGz6IiJyQwlkqZd27p+IwjzWp2HbvqrDG06wZZYPP8+5D7IpPwNO6jcZbioicBoWz\nHGUYWHft/POGDznZFZa5I1pQOmz44RAuH+jhaRWpIBYRqSIK5/rKMLDu2I59TUr5qenU1djTUrHu\n21dhmTsyitK/jDx853T5NWJPRAuTihYRqR8UzvWBxwObNhGw6JcKN2xZDxyosMzdpi2lffvjjIv3\n3jVtNG9uUtEiIvWXwtnXuN3YNm/604YPOApp9LtlrvbRlA0+D1e3eO9RsdGkqWlli4jIUQrnuszl\nwrZhPfa0VPxSVx+dM11c7F1iWCy4O3bCenZPHDGHp2t1j8MIaXSCNxYRETMpnOuKsjLs69dW2IfY\nvjYDS0mJd4lhs+Hu1Ll8D+L4BFzdE3DFdoPgYMLCQjik0ZYiInWCwrk2Kikp3/Dh8GhLe2oK9nUZ\nWJxO7xLDzw9X567em7RccfG4unaDBg1MLFxERKqCwtlsRUXYM9LLj4TXpJbvRbxhXcU50wEBuLp1\nP7oPcXxC+ZzpgAATCxcRkeqicK5BFkch9rQ15TdpHdnwYdNGLB6Pd43RoAGuxB7eiVreOdN+fiZW\nLiIiNUnhXE0sBQfKg/jI9eHUFGxbMits+OBpGIyzV+/fnZpOwN2xk+ZMi4jUcwrnKmDZt6/82vDh\njy/5rUnBtm1rhTWeRo1x9utfccOH9tGaMy0iIn+icD5Flpwc/NasPjrMY00Ktp1ZFdZ4QkMpGzgY\nV1yCdxtET9t2Gm8pIiInReF8PIZRvuHDkX2ID981bdu7p8IyT1g4pUPPLz8a7p5QvuFDZJSCWERE\nTttJhfPkyZNJTU3FYrGQnJxMXFwcANnZ2dx///3edVlZWdx33304nU5mzJhBmzZtAOjbty+33npr\nNZRfRQwDtm/Hf9Gv2A8fFfutScWam1NhmbtlK0r/MsI72tIVF4+nRUsFsYiIVKlKw3nZsmVs376d\nuXPnkpmZSXJyMnPnzgUgIiKC999/HwCXy8W1117LkCFD+OabbxgxYgQTJ06s3upPh2Fg3bb18FSt\no0fF7N9P498tc7duQ+nIiw9fH47H2T0BIzzctLJFRKT+qDSclyxZwtChQwGIjo6moKAAh8NBcHBw\nhXWfffYZw4cPp2HDhtVT6enweLBtySzfcWlN6uGbtlKxHiyosMzdth0MHYqjU2z5Z4i7x2GENjOp\naBERqe8qDee8vDxiY2O9j0NDQ8nNzf1TOH/88ce89dZb3sfLli1j/PjxuFwuJk6cSNeuXauw7BPz\n/+Zrgl55EVt6GtYih/f3DYsFd3QHyoYO814fdnWPw2jcROMtRUSk1jjlG8KM331O94jVq1fTvn17\nb2DHx8cTGhrKoEGDWL16NRMnTuTzzz8/4fs2bRqE3V5Fn+/95X+wfCl06QJJSdCjByQlYUlIwB4S\nctymw8JCqubr11K+3h/4fo/qr27z9f7A93usqf4qDefw8HDy8vK8j3NycggLC6uw5ocffqBPnz7e\nx9HR0URHRwOQmJjI/v37cbvd2E4wXCM/v/i4z52yJ56Dh5/683jLEqDk2EfHYWEh5PrwkbOv9we+\n36P6q9t8vT/w/R6rur8TBX2lEzD69evHN998A0BGRgbh4eF/OqWdlpZG586dvY9nzpzJF198AcDG\njRsJDQ09YTBXOYtFc6dFRKTOqvTIOSkpidjYWEaNGoXFYmHSpEnMmzePkJAQhg0bBkBubi7Nmh29\ngeqiiy7igQceYM6cObhcLp5++unq60BERMTHWIxjXUQ2gdmnQnQ6pu7z9R7VX93m6/2B7/dYq05r\ni4iISM1SOIuIiNQyCmcREZFaRuEsIiJSyyicRUREahmFs4iISC2jcBYREallFM4iIiK1jMJZRESk\nlqk1E8JERESknI6cRUREahmFs4iISC2jcBYREallFM4iIiK1jMJZRESkllE4i4iI1DJ2swuoTpMn\nTyY1NRWLxUJycjJxcaG6XYMAAAjrSURBVHHe52bPns38+fOxWq1069aNhx56CJfLxUMPPcSOHTtw\nu91MmDCBnj17cu2111JcXExQUBAAEydOpFu3bma15XWq/c2bN48ZM2bQpk0bAPr27cutt97K+vXr\neeyxxwCIiYnh8ccfN6OdPznV/l577TUWL14MgMfjIS8vj2+++YYhQ4bQokULbDYbAFOnTiUiIsKU\nnv7oRD0uXLiQ1157DX9/f0aOHMno0aOP+5o9e/YwYcIE3G43YWFhPP/88/j7+5vVltfp9Pfcc8+x\ncuVKXC4XN998M+effz4PPvggGRkZNGnSBIDx48czaNAgM1qq4FT7W7p0KXfffTcdO3YEoFOnTjzy\nyCM+8/37+OOPmT9/vndNeno6q1evrrU/QwE2btzI/7d3/yFNfX8cx59Tp1mpNctRmlj+kfWPCBWZ\nOVtlZIQVQSCJ/TAisoKisqJc/4RWFv0mmwZSltGMiJKUyCByWYIUGmUKkf1OrXRp6db5/CFeNH/l\nvnznHOfx372Xc7kv3zvn3J171c2bN7N27VrlM9iptLSU48eP4+7ujk6nIyUlBXBQHxQuqqysTGzc\nuFEIIURNTY1YtWqVcqy5uVno9XrR3t4uhBBi3bp1oqKiQphMJmEwGIQQQlRXV4uVK1cKIYRITEwU\nr169cmyAAdiTr6CgQGRkZPQ4V2Jionj27JkQQogdO3aIBw8eOCBB/+zJ19WNGzeE0WgUQgih1+uF\nxWJx0JX/u/4y2mw2odPpRENDg7DZbGL9+vXi48ePfbbZs2ePKCwsFEIIcezYMZGXl+fgND3Zk89s\nNosNGzYIIYRobGwUMTExQgghUlNTxf379x2eoT/25Hv8+LHYunVrj3O5Sv3+bn/w4EEhhHOOoUII\n8fPnT5GYmCj2798vLl261ON4XFyc+PDhg7DZbCIhIUG8fv3aYX3QZZe1zWYzCxcuBCA0NJQfP35g\nsVgAUKvVqNVqWlpasFqttLa24ufnR3x8PHv37gVAo9Hw/fv3Ibv+gdiTrzdtbW28f/9euSPW6/WY\nzWbHhOjH/5LParVy9erVHnfBzqa/jN++fcPX1xeNRoObmxuzZ8+mtLS0zzZlZWUsWLAAGB417Cvf\nzJkzOXnyJAC+vr60trZis9mGLEN/7MnXF1epX1dnz55l8+bNDr/uwfD09MRoNBIQENDjWF1dHX5+\nfkyYMAE3NzdiYmIwm80O64MuOznX19czduxYZVuj0fD161cAvLy8SElJYeHChej1esLDw5k8eTJq\ntRovLy8AcnNzWbp0qdL+1KlTrF69mrS0NH79+uXYML2wJx/AkydPSE5OZs2aNbx48ULpZJ38/f2V\n8wwle/MBFBcXM3fuXEaMGKHsMxgMJCQkkJmZiXCSP4rXX0aNRsPPnz958+YN7e3tlJWVUV9f32eb\n1tZWZQltONSwr3zu7u7K0qfJZEKn0ymPIy5fvkxSUhLbt2+nsbHR8YH+Yk8+gJqaGjZt2kRCQgKP\nHj0CcJn6dXr+/DkTJkxg/Pjxyj5nG0MBPDw8uo0TXX39+hWNRqNsd+Z3VB906WfOXXUdkC0WC1lZ\nWdy9e5fRo0ezZs0aXr58SVhYGNDxPLOqqorz588DkJSUxNSpUwkODsZgMJCXl0dycvKQ5OjLv+QL\nDw9Ho9Ewb948KioqSE1NJTs7u8/zOJPB1K+goKDbc/Nt27YRHR2Nn58fKSkpFBUVsXjxYodnGEjX\njCqVioyMDPbt24ePjw9BQUEDtulvnzMYTL579+5hMpm4ePEiAMuWLWPMmDFMmzaNCxcucObMGdLS\n0hx6/QP5l3whISFs2bKFuLg46urqSEpKori4uM/zOJPB1M9kMrFixQpleziMofb6f/VBl/3mHBAQ\n0O1O7suXL8pdXG1tLZMmTUKj0eDp6cmMGTOorKwE4Pr169y/f59z586hVqsBiI2NVV6imj9/PtXV\n1Q5O05M9+UJDQ5WXaCIiImhsbGTs2LHdlu8/f/7c6xKPo9lbv5aWFj59+tRtsFi+fDn+/v54eHig\n0+mcon7Qf0aAWbNmceXKFbKysvDx8SEwMLDPNiNHjlS+jQyHGkLv+QAePnzI+fPnMRqN+Pj4ABAZ\nGcm0adOA4dEHofd8Wq2WJUuWoFKpCA4OZty4cXz+/Nml6gcdy/QRERHKtjOOoQP5O39nXRzVB112\nco6KiqKoqAiAqqoqAgICGD16NACBgYHU1tYqP8jKykpCQkKoq6sjPz+fM2fOKMvbQgjWrl1LU1MT\n0PGh63zTcijZk89oNHL79m2g4w3FzsltypQplJeXAx1LwtHR0UOQqDt78gG8fPmSKVOmKOdpbm4m\nOTmZtrY2AJ4+feoU9YP+MwJs2LCBhoYGWlpaKCkpITIyss82c+bMUfYPhxpC7/mam5s5cuQIWVlZ\nypvZAFu3bqWurg4YHn0Qes9369YtcnJygI5l04aGBrRarcvUDzomplGjRilLvM46hg4kKCgIi8XC\nu3fvsFqtlJSUEBUV5bA+6NL/lSozM5Py8nJUKhUGg4EXL17g4+NDbGws+fn53LhxA3d3dyIiIti9\nezfHjx/nzp07TJw4UTlHTk4O9+7dIzs7G29vb7RaLYcOHcLb23sIk3UYbL5Pnz6xa9cuhBBYrVbl\nVwBqampIS0vjz58/hIeHKy/FDbXB5gMoKiqitLS027J2bm4uN2/exMvLi+nTp3PgwAFUKtVQxeqm\nv4zFxcWcPXsWlUrF+vXriY+P77VNWFgYX758ITU1ld+/fzNx4kTS09OVlZ+hNNh8165d4/Tp093e\nITh8+DBv377l6NGjeHt7M3LkSNLT0/H39x/CZB0Gm89isbBz506amppob29ny5YtxMTEuEz9oONm\n+cSJE90emRUWFjrlGFpZWcnhw4d5//49Hh4eaLVa5s+fT1BQELGxsTx9+pTMzEwAFi1apCzFO6IP\nuvTkLEmSJEnDkcsua0uSJEnScCUnZ0mSJElyMnJyliRJkiQnIydnSZIkSXIycnKWJEmSJCcjJ2dJ\nkiRJcjJycpYkSZIkJyMnZ0mSJElyMv8Brx7UCdNNNogAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 721
+ },
+ "outputId": "1ac0165b-88d3-4306-da91-e1c6cdba4c75"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0575,n_epochs=1000)"
+ ],
+ "execution_count": 127,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07239858\n",
+ "Loss after epoch 50 is 0.015752953\n",
+ "Loss after epoch 100 is 0.0077023986\n",
+ "Loss after epoch 150 is 0.0037670603\n",
+ "Loss after epoch 200 is 0.0018433541\n",
+ "Loss after epoch 250 is 0.00090298854\n",
+ "Loss after epoch 300 is 0.00044331065\n",
+ "Loss after epoch 350 is 0.00021860642\n",
+ "Loss after epoch 400 is 0.000108763714\n",
+ "Loss after epoch 450 is 5.506931e-05\n",
+ "Loss after epoch 500 is 2.8821923e-05\n",
+ "Loss after epoch 550 is 1.5991303e-05\n",
+ "Loss after epoch 600 is 9.719664e-06\n",
+ "Loss after epoch 650 is 6.6537114e-06\n",
+ "Loss after epoch 700 is 5.155091e-06\n",
+ "Loss after epoch 750 is 4.4224894e-06\n",
+ "Loss after epoch 800 is 4.064544e-06\n",
+ "Loss after epoch 850 is 3.88946e-06\n",
+ "Loss after epoch 900 is 3.8038895e-06\n",
+ "Loss after epoch 950 is 3.7620573e-06\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 3.226303e-06\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFKCAYAAAAwrQetAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XdgU/X6x/F3RnfTkdKyyizIFGSI\nQBkCBQco4EWsgIgsmbJklVGQvbcICMIVkHoRBAUBQVCRUjYIyipQdptOmqZpm/H7g3vzEwXKaEmT\nPq9/zOnJOXmeHukn33OS81VYrVYrQgghhCjwlPYuQAghhBCPRkJbCCGEcBAS2kIIIYSDkNAWQggh\nHISEthBCCOEgJLSFEEIIB6G2dwEPo9Ol27sE/P09SUkx2LuMfCP9OTZn7w+cv0fpz/HldY+BgZoH\nrpORdi7UapW9S8hX0p9jc/b+wPl7lP4c37PsUUJbCCGEcBAS2kIIIYSDkNAWQgghHISEthBCCOEg\nJLSFEEIIByGhLYQQQjgICW0hhBDCQRTom6sURIsWzePcuT9JTk7CaDRSokRJfHx8mTp1Vp7sv0OH\nNwgKKopS+f/vpxYvXv7U+92//2deeqkhd+6ksXLlMkaMGPPU+xRCCPFsPVJonz9/nn79+tGtWze6\ndOlyz7oDBw4wd+5cVCoVTZo0oX///gBMnTqVkydPolAoiIiIoEaNGty6dYsRI0ZgNpsJDAxk1qxZ\nuLq65n1X+WjgwCEAbN/+HZcuxTJgwOA8f43Zsxfi6emZp/vcsGEdtWu/SEBAEQlsIYRwULmGtsFg\nYNKkSTRo0OC+6ydPnszKlSspWrQoXbp04ZVXXiE5OZm4uDiioqKIjY0lIiKCqKgoFi5cSKdOnXjt\ntdeYO3cuGzdupFOnTnnelD0cO3aEDRvWYjAYGDBgCMOGDWDbtj0AjB07grfe6kjlylWYOnUi6enp\nmM1mBg8eToUKFR9p/61bt/jH/o4fP0pGhp6rV+O4ceM6H300jAYNQtmxYxsbN0ahUCgID+9MTk4O\nf/xxmo8//ohRo8YxceJYVq78kmPHjvDFF8uwWhUEBgYxevR4du/eyalTJ0hNTeHq1Tg6dXqPNm3a\n5dvvTQghxKPLNbRdXV1ZsWIFK1as+Me6a9eu4evrS/HixQFo2rQp0dHRJCcnExYWBkBISAhpaWno\n9XpiYmKYOHEiAM2aNWPVqlVPFdoTDozlu9hvn3j7+3kjpB0TGk5+om1jYy/y1VebHnj24Ouvv+Kl\nlxryxhvtuHz5EgsWzGb+/E+fplwSEuKZPXshBw8eYMuWb6hZ8wVWr/6cNWu+Ijs7hylTIpk+fS6f\nf/4Zs2cvJC0t1bbt7NnT+Pe/16BWezN37gx+/HEHCoWC2NiLfPbZKq5fv0ZkZISEthBC3EdaVio/\nXN5GN5/Oz+w1cw1ttVqNWn3/p+l0OrRarW1Zq9Vy7do1UlJSqFat2j0/1+l0ZGZm2gItICAAnU73\n0Nf29/d86D1dPT1cUSoVubXwWDw9XP9xs/b73bxdo3HH0/P/n+vn50nVqlUoWTIAAIVCYVvn5uaC\nn58n586dITk5mb17dwGQlZX5j32rVEpGjx6CSnW3b39/fxYuXHjf/Xl5udGgwUsEBmqoVKkcWVmZ\npKUlULFiBYKDAwFYuXKFbb9FinijUuWgVitxcTGjVqtsb7hefrkxhw8fpmrVqrz4Yh2KFfNDo3Eh\nMzPjoTevdwSOXn9unL0/cP4epT/HYrVaiToTxZCdQ7itv03xgCJ0qNrhmbz2M/kgmtVqfaSf/V1u\ns6aMqDWeEbXGP3FdD/LX2cUCAzX3nW0sPd2IwZBtW5eaasBqVdiWrVar7XFGRqZt/cCBw6hevcZ9\nXwvAbLYwbdq8e65p63Tp991fRkYWLi4e6HTppKRkkJ1tIi3NiNGYfd/9JibqSUvLwGSykJSUgclk\ntu0/KekORqOJ9HQj2dkWdLp0DAYDZrOlQMy29qQedPychbP3B87fo/TnWC6nXWLkL0PZd+0n3FXu\njHkpkvaV2+dpj/k2y1dQUBCJiYm25fj4eIKCgv7x84SEBAIDA/H09MRoNN7zXGelUCgwGo0YjUbO\nnz8HQNWq1fnll30AXL58iQ0b1j7V/u6nTJmyXL0ah8FgICsri8GD+2G1WlEolJjNZtvzfHx8UCgU\n3Lx5E4ATJ45RuXKVJ+hUCCGcX5Y5i7lHZtJ0Q332XfuJ5qXD+CU8hkF1hqFSOsgsX8HBwej1eq5f\nv47JZGLv3r2EhoYSGhrKzp07AThz5gxBQUF4e3vTsGFD28937dpF48aNn76DAqpduw707v0+U6dO\npFKlu2HYocM73LhxjX79ejJjxmReeKH2U+3vfjw8POjRow+DB/dj4MAPeeONdigUCmrVqk2/fj3u\nuaY9YsRYhg0bxoABvTGZTLRo0erJGxZCCCd14MZ+mkeFMv3QZHzcfFnRajVftf6Gsr7lnnktCmsu\n56lPnz7NjBkzuHHjBmq1mqJFi9K8eXOCg4Np2bIlhw8fZvbs2QC0atWKHj16ADB79myOHDmCQqEg\nMjKSypUrk5CQwMiRI8nKyqJEiRJMmzYNFxeXB752QTil4myndv5O+nNszt4fOH+P0l/BlWpMYfyB\nCDacXYcCBR9U70nES+PxcfMFQHntKu5frcVr2CB0Kq88e92HnR7PNbTtqSAcaEf+H+5RSH+Ozdn7\nA+fvUformEwWE29tacPBWweoXqQGs5vOp3bRundXWiy4r16J16RIlBl6+O47dC81zbPXflhoyx3R\nhBBCiL+Zc2QGB28doE35tixv9QVq5d24VF6KRTNkAK7Rv2Hx8+PO4mX4tG4NifpnUpeEthBCCPEX\nv934lblHZlJKU5p5zRbdDWyzGY8VS/GaNglFZiZZr7VBP3MulqLFQJG3Xz1+GAltIYQQ4r+SMpPo\nu7snSoWSz1quxNfND9X5c2gG9cPl6GEsAQGkL/iUrLZvPdOw/h+Z5UsIIYTg7v01Bv3Ul9sZtxj9\n0jheLFIHj4Vz8W/RCJejhzG2e4vkXw+T1e5fdglskJG2EEIIAcCKU0vZFbeDJsHNGOwahs9rLXA5\neRxLYBB3Zs4ju/Ub9i5RQvtx3bp1k65dw6lUqTIA2dnZdO78Pk2bNnvsfX3zTRSpqak0afIyv/yy\njx49Przv8/43rebDvh73P5cuXWTu3Jn/mM6zadOXeP75mrblgIAAJk6c9tg1/93evbtp1iyMCxfO\nPbQHIYQoyE7pTvBJ9HiKuwTw9enqaPs2Q5GTg/HtcPSTp2P11+a+k2dAQvsJlC5dxhaKd+6k8cEH\nnalfvwFubu5PtL+KFStRsWKlB67/37SajxLaD+Lt7Z0n83L/3dq1a2jWLCzXHoQQoqDSZ6fTe9cH\nVL+ezZ693vhdWIS5REn0s+eTHfaKvcu7h4T2U/Lx8SUgoAhJSUl88cUK1GoX7txJ5ZNPpjNz5hRu\n3ryByWSiZ88+1KnzIkeOHGLhwjlotQEEBBShRImSHDt2hE2bvmby5JkPnVZzwYKlbN26md27d6BQ\nKGnc+GXefbcLCQnxjBs3ChcXFypUeO6Ra7916yYffjiaZcvWANCjx3tMnjyDVauWU6RIIOfO/Ul8\n/G3Gj59MpUqVWbduDfv27UGhUNKnzwDOnv2DixfPExExnA4d3rH1sGfPj0RFrUOlUlGpUhUGD/6Y\nlSuX3XcaUSGEsLdxe4bQ45tYRh5QoLLEkfleNzIiJ2H18bV3af/g0KHtNWEsbt/l7dScWW+0I2PC\no0/NeevWTe7cSSMoqChw957eI0eOYceObQQEFGH06PGkpqYyaFAf1qzZwLJlixk3bhIVKz7Hxx9/\nRIkSJW37MhgyHjqtpk6XwL59e/j005UA9O3bg2bNwti0KYoWLVrRseO7rF27mosXzz/17yE7O5u5\ncxfz7bcb2bFjG56enuzbt4dly1Zz8+YN1q5dzahR41i3bg1Tp87i2LEj/+3BwPLlS/jii/V4enoy\nYsQQ27q/TyMqoS2EsLefN00hYuzXVE0EU6lSpM5dRM4TXO58Vhw6tO3l6tU4BgzoDdydb3zs2Im2\n6UurVr07Jenp06c4efI4p06dACArK4ucnBxu3bpFxYp3R8MvvFCbrKws236vXLlM6dJlcXNzx83N\nnenT597zun/+eYbr168xcODd68YGQwa3b9/kypXLNGt2d/7yWrXqcvDggX/UrNfrbTUDhIRUIDy8\nywN7rFmzFgCBgUX5448znD9/jqpVq6NUKgkOLsWoUePuu921a1cJDi5tm6WsVq06nD9/FoAaNV4A\n7k40o9c/mxsRCCHEfRkMmCZ+zFur16K0Qvx74SgnzgVvb3tX9lAOHdoZEyY/1qg4r/z1mvbfqdUu\ntv927dqdli1fvWe9Uvn/37L7+x1klUoVVqvlga+rVrvQoEEoI0aMuefn69atQaFQ/nef99/+fte0\nb9++dc+yyWSyPf7ffN7/q1OlUmKx5H7HW4Xi3r5Mphzc3Nzuu08hhMhvFquFW/qbXL5ziStpl7mc\ndgnPmEP0XXGYMrpsLmjhz0kjaPD2WHuX+kjke9r5pGrV6uzf/zMAKSnJLFu2BIAiRQK5evUKVquV\n48eP3rNNbtNqVqpUhWPHjmI0GrFarcyfP5usLCOlS5fh7Nk/AGynoh+Fp6cXSUlJWK1WkpISuXnz\n+gOfW6lSFX7//SQmk4nk5CRGj/4Y4B9BXqpUGa5fv4rBkAHA8ePHqFSp6iPXJIQQeeHqnTjabGpF\nmeVFqfVlVd7a0oZxOwdScco8pk/9jeDEbL5oHsBXqyIcJrDBwUfaBVnz5mEcO3aYPn26Yzab6d79\n7qnp3r37MXbsSIoVK267Dv4/f51WE+CddzrdM63mokXL6djxXfr374VSqaRJk5dxc3Pn7bffZdy4\nUfzyy15CQio+co0+Pj40bNiQnj27UqFCxYd++rt48RK88srrDBjQG6vVyocf9gfguecq0atXV/r2\n/cjWQ//+gxg2bCAKhZIaNV6gZs0XOHIk5rF+f0II8aSup1/jrS1tuJoex/NFahLiF0Kryyo6ffET\nvreTMFYIwbBgGW1erGfvUh+bzPKVC0edoeZRSX+Ozdn7A+fvUfrLWzf1N2j37etcuXOZkfXG8PFz\nffCaOA6PL1djVakwDByCYegIcH+yr+jeT173KLN8CSGEcHq3M27x1pY2XLlzmWF1RzI6rRbeTeqj\nunkDU9XqpC9Ygum/H7J1VBLaQgghHF68IZ63trThUlosERX7M/bfV/H4egZWtZqM4aMxDBoGrq72\nLvOpSWgLIYRwaDqDjg5b3uBi6gWWGdvQY8hGVAnx5NSsRfr8JZirVbd3iXlGQlsIIYTDSspMosPW\nN0m6fpZD0RV4cf/3WN3c0I+dQGa/j0DtXDHnXN0IIYQoNFKMyXTY8gbP/3KGz3e5o7lzkZy69e6O\nrp9zzrkQJLSFEEI4nGRjEv3WtmHSv8/Q/ixYPRToJ00js2cf+MuNnJyNhLYQQgiHcujmQXZNf4f/\nfJuC1gjZDUNJn7sYS/kQe5eW7+SOaEIIIRyCxWphza6JKN5uxYINKXgpXLkzYw5pm7YVisAGGWkL\nIYRwAIkGHT9EtqHXhj/xzYKE+rVQLfkSS6nS9i7tmZKRthBCiALtxOFN6MKqMHTNn6iUam7OnI5i\ny75CF9ggI20hhBAFlNmUw6FJnWi+cife2XCu3nNol3+LS4lge5dmNzLSFkIIUeDoTu0nvml53ly6\nE5NKwYkpI9F+dxgKcWCDjLSFEEIUEPEZt9l2YTMeyz+l17dxeJhgf52iFF/2HSVLV7Z3eQXCI4X2\n1KlTOXnyJAqFgoiICGrUqGFbt3v3bpYuXYqrqyutW7emS5cu/Oc//2Hr1q2255w+fZrjx4/z3nvv\nYTAY8PT0BGDkyJFUr+48t5cTQgjxeOIN8Xwfu4XvYr8l9cR+Vm6B+jcgRePCvmHvU6fPbBRKOSn8\nP7mG9qFDh4iLiyMqKorY2FgiIiKIiooCwGKxMGnSJDZv3oyfnx+9evUiLCyMt99+m7ffftu2/Q8/\n/GDb37Rp03juuefyqR0hhBAFncVq4T/nNrDh7DoO3NyPymxl+AGY8LMCV5OV1DfbYJ6+kLpFiti7\n1AIn17cv0dHRhIWFARASEkJaWhp6vR6AlJQUfHx80Gq1KJVK6tevz4EDB+7ZfsmSJfTr1y8fShdC\nCOFort6J4+2tbRn4Ux9+u/krnUzPc3VDSabuAVVAUdLWfEXO5+uxSmDfV66hnZiYiL+/v21Zq9Wi\n0+lsjzMyMrhy5Qo5OTnExMSQmJhoe+6pU6coXrw4gYGBtp8tXLiQzp07M378eIxGY172IoQQooCy\nWq18+cdqmkY14NcbP9M6+BVuJvfly+l/UPzCDYzhnUn5NYbs11rbu9QC7bE/iGa1Wm2PFQoF06dP\nJyIiAo1GQ3DwvZ/q27hxI+3bt7ctd+3alUqVKlG6dGkiIyNZt24dPXr0eOBr+ft7olbb/x6ygYEa\ne5eQr6Q/x+bs/YHz9+js/WW5pdFza092xu7E182X7ypE0nrGJhS/74RSpWD5ctxffRV3exf6FJ7V\nMcw1tIOCgu4ZPSckJNwzcq5Xrx7r168HYM6cOZQsWdK2LiYmhrFjx9qWW7ZsaXvcvHlztm/f/tDX\nTkkxPEIL+SswUINOl27vMvKN9OfYnL0/cP4enbk/q9XKDzc389EPg7iTnUarYi/z5fEKBI6ZhMJi\nIbNrdzIiP8Gq8QEH/h3k9TF82BuAXE+Ph4aGsnPnTgDOnDlDUFAQ3t7etvU9e/YkKSkJg8HA3r17\nadCgAQDx8fF4eXnh6uoK3D143bp1486dO8DdQK9YseKTdyWEEKLAijfE0/WHcLpt6YbZamZ9kcFs\nm32DoGWfYwkuTeo336GfPf9uYItHlutIu3bt2lSrVo3w8HAUCgWRkZFs2rQJjUZDy5Yt6dixI927\nd0ehUNC7d2+0Wi0AOp3O9hjunkrv2LEj3bp1w8PDg6JFizJw4MD860wIIYRdnEk8zVtbWpOSlcKr\nxZuw+mAZglYvAMDQqw8Zo8fDXwZ/4tEprH+9SF3AFIRTRs586gqkP0fn7P2B8/fobP3ps9NpubEp\nsakXWePdi/eW/oQiNhZT+RDS53+KqX4De5eY557l6XG5I5oQQog8YbVaGf7zEOLjL7Lv+PM03bEC\nlEoM/T4iY+QY8PCwd4kOT0JbCCFEnvjq7FrSdnzNuW2ulEj+HVOlyqjXrCajfFV7l+Y05N5wQggh\nntqFuMP4DP2IH7+E4mlmMoZ8TMruX+Gll+xdmlORkbYQQoinYvlhC+U/+oCGaWaSK5ZB8dlaTM/X\ntHdZTklG2kIIIZ6IIjkJTb9eFH3/PbTpJraEv4h571EJ7HwkoS2EEOKxuX6/FW3jl3DfGMXhEtBp\nVGXqzNsO/703h8gfcnpcCCHEI1PodHiP/hj3rZuxuLoy9hUXljRyZ1d4FG4qN3uX5/QktIUQQuTO\nasVt80a8I4ajTE4mq05d3no1le0uF/m8xeeU9S1n7woLBQltIYQQD6WMv4338CG47diG1cMD/aRp\n9K94lu1n19CtWg/erNA+952IPCGhLYQQ4v6sVtyi1uM1bhSqtDRu1KrEmn5N2O/6Gz+c/Z7qRWrw\nSeg0e1dZqEhoCyGEuMfBmwc4ELOOdou289LpJNJdYXhrWF7nHNYb5wAo6R3MilZf4K525Ak1HY+E\nthBCCJsfL//Ar1PeZcYOCz7ZsO85V5Z0r4WmwvNM8XuOiv6VqOj/HMW9SqBQKOxdbqEjoS2EEAKA\nEzH/ofigXiy9ZCHb25OEaZOo1qUnn0o4FxgS2kIIUdhZLCTOH0fDOYvwyoEbjevivngtiuIl7F2Z\n+BsJbSGEKMRUsRdQDehOlaMnSfKAw2P6UK3vDCwyui6QJLSFEKIwMpvx+GwJntMnoczKYmMVSJk6\njXah/e1dmXgICW0hhChkVOfOohnUF5djR0n0VtLnTXih9zQ+rCmBXdDJvceFEKKwyMnBc/5s/Fs0\nwuXYUbbW9aFyXwvl3h8lge0gZKQthBCFgOr3U2gG98fl95OYihbl4/ZeLCh2id41+jL8xdH2Lk88\nIgltIYRwZtnZeM6diefCuShMJpI6tOfdRjf5MTWG8Mqd+SR0mnzf2oFIaAshhJNSHz+KZnB/1H/+\ngalECVZ+2IDBym0YU420Kd+WuS8vQqmQq6SOREJbCCGcjdGI16xpeCxZgMJi4WTbRrSvfZbL1m8o\n5l6ciJfG07HSuxLYDkhCWwghnIj6UAyawf1QX7yAvmRRBrT3YE2R/XiqPBlRK4K+LwzEy8XL3mWK\nJyShLYQQziAjA69pn+Cx4jMANoWV5r16V8l0VfBu5S6MfmkcxbyK27lI8bQktIUQwsG5/PYrmsH9\nUcVd4UYxb95tbeDXUldpVLIJE0On8nyRGvYuUeQRCW0hhHBQCn06HhPH4bVmFWYFzAiFCS/rKVe0\nGl/WH0+rMq/KJ8OdjIS2EEI4oOxdW/AaOgCvhDROB0L3dqANfY11NfrRqGQTCWsnJaEthBAO5Pr1\nU6QP606TvefJUcK0l12I69OVRbX7U96vgr3LE/nskUJ76tSpnDx5EoVCQUREBDVq/P/1kd27d7N0\n6VJcXV1p3bo1Xbp0ISYmhkGDBlGxYkUAnnvuOcaNG8etW7cYMWIEZrOZwMBAZs2ahaura/50JoQQ\nTsRsMbN3+SCazvo3tdLhdAkX9o/rzdttRuLr5mfv8sQzkmtoHzp0iLi4OKKiooiNjSUiIoKoqCgA\nLBYLkyZNYvPmzfj5+dGrVy/CwsIAqFevHgsXLrxnXwsXLqRTp0689tprzJ07l40bN9KpU6d8aEsI\nIZzH+YsHSBvUiXcPJ5OtgoM936RM5Ar+5eZh79LEM5brN+ujo6NtQRwSEkJaWhp6vR6AlJQUfHx8\n0Gq1KJVK6tevz4EDBx64r5iYGFq0aAFAs2bNiI6OzosehBDCKWWZs9g+rysVWr7K64eTuVBey/Ud\nOwmZuha1BHahlOtIOzExkWrVqtmWtVotOp0Ob29vtFotGRkZXLlyhZIlSxITE0O9evUoWbIkFy9e\npE+fPqSlpTFgwABCQ0PJzMy0nQ4PCAhAp9M99LX9/T1Rq1VP2eLTCwzU2LuEfCX9OTZn7w+cv8f7\n9Xf0+HYSe4Tz/vF0jGr4c0R3qkxZBmrH+yiSsx8/eHY9PvbRt1qttscKhYLp06cTERGBRqMhODgY\ngLJlyzJgwABee+01rl27RteuXdm1a9cD9/MgKSmGxy0vzwUGatDp0u1dRr6R/hybs/cHzt/j3/vL\nyNazZ3ZX2i7bTZ1MuFC5KO7LvqZIlVroUjLtWOmTcfbjB3nf48PeAOR6ejwoKIjExETbckJCAoGB\ngbblevXqsX79epYtW4ZGo6FkyZIULVqU119/HYVCQenSpSlSpAjx8fF4enpiNBoBiI+PJygo6Gn6\nEkIIpxJzbCPnXwmhx/zdeJoV/D6iD357z+JepZa9SxMFRK6hHRoays6dOwE4c+YMQUFBeHt729b3\n7NmTpKQkDAYDe/fupUGDBmzdupWVK1cCoNPpSEpKomjRojRs2NC2r127dtG4ceP86EkIIRxKmjGF\nzeNfpVHb7rQ6k8mF6sGk7jtIsY9ngsr+lwhFwZHr6fHatWtTrVo1wsPDUSgUREZGsmnTJjQaDS1b\ntqRjx450794dhUJB79690Wq1NG/enI8//pg9e/aQk5PDhAkTcHV1ZeDAgYwcOZKoqChKlChBu3bt\nnkWPQghRYP24dyUuffrR+3w2enclf44fQpF+40ApM3CJf1JYH+Xisp0UhOsgzn49RvpzbM7eHzhv\nj4kZCfz8ydt0XnccTTacr1Me3882oyxTzt6l5SlnPX5/VaCuaQshhMg7VquV3fs+JbFFZfp8cRyr\nWsX5qePx337c6QJb5D3H++6AEEIUYNnmbFKyUkg1ptj+m5qVQrIxmTRDMuU3bOWDby7glQPnGlSh\nwtc78Zc7molHJKEthBB5wGq1Mi1mEguPz8Vitfxj/XOJsHILNLoGqd5qLs6YhLZzP1RBPuDkp49F\n3pHQFkKIp2S1WvkkejxLTiwg2LsUdYq+iJ+7P/5u/vi7+NB863Hqr/oedVYOia+GYZ39Gb7ylVfx\nBCS0hRDiKVitViYdjGTJiQVU8KvI5rbbKOpVDADVn3+gGdwPl+PHsBQJJO3TuVjfaGvnioUjk9AW\nQognZLVamXxwAouPzyfEr8L/B3ZODp6L5uE5ZwaKnByMHd5BP3k6Vm2AvUsWDk5CWwghnoDVamXK\nwYksOj7vnsBW/34S70H9cTl9CnOx4uhnzye71Wv2Llc4CfnKlxBCPCar1crUmE9YeHwu5X1D2Nx2\nG8XUWjynT8Kv1cu4nD5FZueupPwaI4Et8pSMtIUQ4jH8L7AXHJtjC+zgczfQDGqL+txZzMGlSJ+z\nkJxmLexdqnBCMtIWQohH9L+vdS04NodyvuX59pVvqDBnKX6vh6E+d5bMbj1I+eWgBLbINzLSFkKI\nXGSaMjlw41e+ufAfNp6PoqxPOXaWnES5Nzqgjr2IuUxZ0ucvISdUJkES+UtCWwgh7uNK2mX2XN3F\n7rhd/HbjV4zmu9MKV/coz0+nQikyrAsAhg/7kTFqHHh52bNcUUhIaAshxH8djT/Mtxc3sSduFxdT\nL9h+XkVblealWxKeUJT6k5ehvvolpgoVSZ//KaZ6L9mxYlHYSGgLIQTw09UfCf/+XwB4qr14tezr\ntCjTihalW1IKX7w+icRjzQKsSiWGj4aS8fEocHe3c9WisJHQFkIUevEZtxmw50Ncla4sa/UFYWVa\n4aZyA8Dlpx/RDBuE6sZ1TFWqkj5/CaZadexcsSisJLSFEIWa2WKm3+5eJGYmMqXRDFqXfwMARWoK\n3uMjcN+wDqtaTcawkRiGDAdXVztXLAozCW0hRKG24Ngcfr3xM6+Wa03P5/sA4LpjO97DB6OKv03O\n8zVJX/Ap5urP27lSISS0hRCF2MGbB5h5eColvYNZ0GwJyuRkvMeMwH3Tf7C6upIRMR5D/0Hg4mLv\nUoUAJLSFEIVUsjGJPj/2QIGX5uVGAAAgAElEQVSCpS1XUnTXz2hGDUOZmEhO7Tqkz/8Uc+Uq9i5T\niHtIaAshCh2r1crgn/pzM+MGUyoOodWYT3H7fgtWd3f0kZPJ7NMfVCp7lynEP0hoCyEKnRWnlrLj\n8nY+uV6ZUQtWo0xJIeelBqTPX4w5pKK9yxPigSS0hRCFysmE46zYOZYd21x55c+zWD29SJ82C+MH\nvUAp0zGIgk1CWwhRaOiz7vDj5H9xYrMJvyzIbtyU9LmLsJQpa+/ShHgkEtpCiEJBcTWOtA/CmPF7\nIkYPV9Jnz8L4XjdQKOxdmhCPTM4FCSGcm8XCnSVT8Gz0Ai/8Hs9v1XxJ/fUIxq4fSGALhyOhLYRw\nWrd/309C80qETJxBFmYmvFcGzy2/oSpd1t6lCfFE5PS4EMLpxKff5PTkD3hzbTSeObDneQ3J02fQ\nr25nFDK6Fg7skUJ76tSpnDx5EoVCQUREBDVq1LCt2717N0uXLsXV1ZXWrVvTpcvdOWZnzpzJ0aNH\nMZlMfPjhh7Rq1YpRo0Zx5swZ/Pz8AOjRowcvv/xy3nclhCiUUo0pfP1dJM1n/JvwqxaSvZT8NqYH\nz384A5VKxijC8eX6f/GhQ4eIi4sjKiqK2NhYIiIiiIqKAsBisTBp0iQ2b96Mn58fvXr1IiwsjCtX\nrnDhwgWioqJISUmhffv2tGrVCoChQ4fSrFmz/O1KCFHobDyzjtvThzB6txF3M5x9+QX8Fm3ghaIl\n7F2aEHkm19COjo4mLCwMgJCQENLS0tDr9Xh7e5OSkoKPjw9arRaA+vXrc+DAAdq2bWsbjfv4+JCZ\nmYnZbM7HNoQQhVn0j0upO3wkL94Evb83ulkLCXizg73LEiLP5fpBtMTERPz9/W3LWq0WnU5ne5yR\nkcGVK1fIyckhJiaGxMREVCoVnp6eAGzcuJEmTZqg+u8tAdeuXUvXrl0ZMmQIycnJ+dGTEKKwyMkh\nOXIAr3a9G9g327TEGP07SGALJ/XYF3msVqvtsUKhYPr06URERKDRaAgODr7nubt372bjxo2sWrUK\ngLZt2+Ln50eVKlVYvnw5ixcvZvz48Q98LX9/T9Rq+9//NzBQY+8S8pX059icvT94QI/HjmHs2onA\nM+e4oYHbsydQp3fksy8uDzj7MXT2/uDZ9ZhraAcFBZGYmGhbTkhIIDAw0LZcr1491q9fD8CcOXMo\nWbIkAL/++iufffYZn3/+ORrN3WYaNGhg26558+ZMmDDhoa+dkmJ49E7ySWCgBp0u3d5l5Bvpz7E5\ne39wnx6zsvCcOwPPhfNwN5tZURusk+bS/sWeDvm7cPZj6Oz9Qd73+LA3ALmeHg8NDWXnzp0AnDlz\nhqCgILy9vW3re/bsSVJSEgaDgb1799KgQQPS09OZOXMmy5Yts31SHGDgwIFcu3YNgJiYGCpWlBvz\nCyEenfroYfxbNMJr3mxu+ipp+R5cnTqR9i/2tHdpQjwTuY60a9euTbVq1QgPD0ehUBAZGcmmTZvQ\naDS0bNmSjh070r17dxQKBb1790ar1do+NT548GDbfmbMmEHnzp0ZPHgwHh4eeHp6Mm3atHxtTgjh\nJDIz8Zo+GY9lS1BYLGx8uRgfNLjNu3X7MLDW4Ny3F8JJKKx/vUhdwBSEUyrOfmpH+nNszt4fQODZ\nE5i6fYD6UiymsuUY26k4M1wP0DbkLZa1WoVS4dg3dnT2Y+js/cGzPT0udxsQQhRMej1eUyfCyuWo\nAEOfAQxtrGfZhdWElmjM4rBlDh/YQjwuCW0hhN2dSDjGqF+Goc/R46n2pHGsidFfXsRTl8nNYF9W\n93uZo2Vus+nCRqoGVGfNa+txU7nZu2whnjkJbSGEXe2J20WPne+TaTJQGj+Gf3+HnkfMmBQwrRFM\nbJpGVvYWuAClNKXZ0OYbfNx87V22EHYhoS2EsJsNZ9cxZO8AXJQu7PQdQfNZa1HdTCGnSlUSZs/m\njWoVeVsD1+ITyDQZqBJQDW8X79x3LISTktAWQjxzVquVeUdnMf3QZMpafPnl6EuU2joDq1pNxvDR\nGAYNw9XVlaJAoFaDr7movUsWokCQ0BZCPFNmi5lRv37MmjMr6R5XhKXfW3HV7SKnxgukz1+Cufrz\n9i5RiAJLQlsI8cwYcgz02d2Dw6e3sW2PL68fS8Tq6op+TCSZ/QeBWv4kCfEw8i9ECPFMJBuT6PJ9\nR8r9dJgLO13wT08jp86LpC/4FPNzlexdnhAOQUJbCJHvrt6JY8D6Nxm9/jJvnQWruwr9xIlk9u4L\nKvtPCiSEo5DQFkLkq8upsayLbM62zSlojZBdvwH6+Uswl69g79KEcDgS2kKIfHP1z/2k9WnPgj+z\nyHJ3JX3aFIwf9AKl3MlMiCchoS2EyHtWK6krZlJx0lR8sqxcqhWC7/LNWMqUtXdlQjg0ebsrhMhT\nyqtxqNqFUXHsFKxY2T70bTQ7jklgC5EHZKQthMgbFgvuq1fi8clY1IZMtleA61Mm0L7ZUHtXJoTT\nkNAWQjw15aVYNEMH4npgPykeCga1hxcHf0p4lS72Lk0IpyKnx4UQT85sxuOzxWibNcT1wH6+q6Km\nen9oMGyFBLYQ+UBG2kKIJ6K6cB7NoH64HDmE0U/Dh2+6sa5KDp+1+oK2Fd6yd3lCOCUJbSHE4zGZ\n8FiyAI9ZU1Fl5/BtTTd6tUonTePC562+pHX5N+xdoRBOS0JbCPHIrkV/R+CwoQRejOe2F/RtDz+/\n4EmbkE50rdqNmkG17F2iEE5NQlsI8VD6HD1rT6zAf/ESeu9MwNUC615Qs6tvazrU6sTiUi1wVbna\nu0whCgUJbSHEfWWZs/j3mVXs2TKNeVGp1EiARH93Dkf0IbTTSFq5eNm7RCEKHQltIcQ9TBYT/zm3\ngYUHptJ923V2HgC1BdLCw2HyLOr6+Nq7RCEKLQltIQQAFquFbZe2Mj1mMtrfz/PdVgVVdJAdHEzq\nvCXkNG1m7xKFKPQktIUQ/HR1N1NjPuHCjRNM2atg0EFQWq1k9uiNfswE8Pa2d4lCCCS0hSjUzBYz\nY38bycrfl9P4CsT+4E3xeD2mcuW5M38JOQ1C7V2iEOIvJLSFKKQMOQb67O7Br2e3sfY3LZ1/Scaq\nNGDoO5CMkWPA09PeJQoh/kZCW4hCSGfQ8d72jvhHH+XCD+4UT0zG9Fwl0ucvwVS3nr3LE0I8gIS2\nEIXMxZQL9NrYno++uUrvY2BV5WAYNIyMYSPB3d3e5QkhHuKRQnvq1KmcPHkShUJBREQENWrUsK3b\nvXs3S5cuxdXVldatW9OlS5cHbnPr1i1GjBiB2WwmMDCQWbNm4eoqN2UQ4lk5eCuaL+f9ix826Sl1\nB3KqVke/8FNMNV6wd2lCiEeQ6yxfhw4dIi4ujqioKKZMmcKUKVNs6ywWC5MmTWLFihWsW7eOvXv3\ncvv27Qdus3DhQjp16sT69espU6YMGzduzL/OhBD32HHsS9Lef42vV+spYVCRMSKC1F37JLCFcCC5\nhnZ0dDRhYWEAhISEkJaWhl6vByAlJQUfHx+0Wi1KpZL69etz4MCBB24TExNDixYtAGjWrBnR0dH5\n1ZcQ4r+sVit7lvQhrEN/upywkFwlhLTd+zF8PArkTJcQDiXX0+OJiYlUq1bNtqzVatHpdHh7e6PV\nasnIyODKlSuULFmSmJgY6tWr98BtMjMzbafDAwIC0Ol0D31tf39P1GrVk/aWZwIDNfYuIV9Jf47t\nYf3FnjvIre4dCT9wDaMabkV8RPGJc0DtWB9nKczH0Bk4e3/w7Hp87H+5VqvV9lihUDB9+nQiIiLQ\naDQEBwfnus3DfvZ3KSmGxy0vzwUGatDp0u1dRr6R/hzbg/q7fucq+xf1JXzFr4QY4FQ5L1w+20CR\nWk3RpWTaodInV1iPobNw9v4g73t82BuAXEM7KCiIxMRE23JCQgKBgYG25Xr16rF+/XoA5syZQ8mS\nJcnKyrrvNp6enhiNRtzd3YmPjycoKOiJGhJC3J/OoOOLPZ8QOvvfDPzTSqaLgphBnSk3ciEKBxtd\nCyH+Kddr2qGhoezcuROAM2fOEBQUhPdfbmnYs2dPkpKSMBgM7N27lwYNGjxwm4YNG9p+vmvXLho3\nbpwfPQlR6KRlpTLt4ETmDavC6P5raPenlRsvVET/yxHKj/lUAlsIJ5Hrv+TatWtTrVo1wsPDUSgU\nREZGsmnTJjQaDS1btqRjx450794dhUJB79690Wq1aLXaf2wDMHDgQEaOHElUVBQlSpSgXbt2+d6g\nEM4sIzuDhcfm8s2+ucz65g6tL0C2uyup0ybj+kFvUOb6vlwI4UAU1ke5uGwnBeE6iLNfj5H+HJPR\nZGTNmZUsOj6XN3/VMWcX+GRBZpOmGOYuxlK6jL1LzDPOegz/R/pzfAXqmrYQouDINmez/s8vmXd0\nFm7Xb7LhexXNYsHs40P6jGkY3+0CCoW9yxRC5BMJbSEcgMliYuP5KGYfns61tDgGH3Nh2m4X3Iw5\nZLV8Bf2s+VhKlLR3mUKIfCahLUQBZrVa2Rq7mRmHpnAx9QJVU1w4u6s4z/15C4ufH6xYxJ1Wb8ro\nWohCQkJbiALqevo1hu4byL5rP+GKinWxLxL+9SmUWbfIav0m6dPnUKR6BXDy64VCiP8noS1EAWOx\nWvj3mS+YGD2OjBw93VQvsWijAe+Th7EUKULakuVkv9ne3mUKIexAQluIAuRK2mWG7hvI/hu/oFX5\n8OONN6m/ZgeK7GyMb3VAP2UW1oAAe5cphLATCW0hCgCL1cLK35cx5eBEDCYDfZShzI1KxeP0VsxB\nRdHPmk/2a63tXaYQws4ktIWws0upFxm0tz8xt6IJUvnxc1wL6nz5AwqTCWN4Z/SfTMXq52/vMoUQ\nBYCEthB2YrVa+eLM50z4bQxGs5FBiqZMX3cb97PfYS4ZTPqcBeQ0b2nvMoUQBYiEthB2kJaVytB9\nH/Fd7LcUV/nzQ2wLaqzfgcJsJrNrdzIiP8Gq8bF3mUKIAkZCW4hn7Hj8UXr9+AFX71yhp+F5Fn2T\ngXvsNsyly5I+bxE5jZvau0QhRAEloS3EM2K1WllxaikTo8fhYsxh35k6NNl6DABDzw/JiIiEv8yg\nJ4QQfyehLcQzkGJMZtDe/uy4vI03b/mybpsH3tePYiofQvr8TzHVb2DvEoUQDkBCW4h8duT2IXrv\n+oDUpGt8E12ct/bdwqpMx9DvIzJGjgEPD3uXKIRwEBLaQuSjlb8vZ9xvo2h2wcSGnT5oE25hqlSZ\n9PlLMNV50d7lCSEcjIS2EPlk6YnFzPkpglV73HnvsAmrKoOMocMxDBkBbm72Lk8I4YAktIXIB0tP\nLCZmdQR/blNSIs2IqdrzpC/8FNPzNe1dmhDCgUloC5HHvvhlJuU+mcz4U2BxUZIxcjSGj4aCi4u9\nSxNCODgJbSHy0N7Ffeg6Zz3FMkBfvSrZS1ZhrlLV3mUJIZyEhLYQeUCh0xHfty0dfzmNUQ1Xh3+E\nx5AJoJZ/YkKIvCN/UYR4GlYrbps3oh4xkGp3DBwu44LrZxsoUUfuGS6EyHtKexcghKNSxt/G5/1O\n+PTpAQYD4970wbLjgAS2ECLfSGgL8bisVtw2rMO/0Yu47djGvjLQfFggbWbvo3xAJXtXJ4RwYnJ6\nXIjHoLx+Da9hA3Hf+xN6NwUft4atTYqxuf12yvtVsHd5QggnJyNtIR6F1Ypi1VK8G9XGfe9P7AyB\nWv3VGN7vxvYOP0lgCyGeCRlpC5GL9HPHMffvSsVTcaS6waD2rijf682mWgMp5lXc3uUJIQoRCW0h\nHiDVkMTxye/Tes0veOXAjsouHB3dh6HNhuHvrrV3eUKIQuiRQnvq1KmcPHkShUJBREQENWrUsK1b\nt24dW7duRalUUr16dcaMGcPSpUs5cOAAABaLhcTERHbu3Enz5s0pVqwYKpUKgNmzZ1O0aNF8aEuI\np3Pw51UEjRhOx8s5JHsq2DXsbV4YMI86rhp7lyaEKMRyDe1Dhw4RFxdHVFQUsbGxREREEBUVBYBe\nr2flypXs2rULtVpN9+7dOXHiBH379qVv374AbN68maSkJNv+VqxYgZeXVz61I8TTSc1IJGbsv/hX\n1HE8THA6tDLapd/QqFgpe5cmhBC5fxAtOjqasLAwAEJCQkhLS0Ov1wPg4uKCi4sLBoMBk8lEZmYm\nvr6+tm1NJhNfffUVXbp0yafyhcg7MT99TnqTSnRZdxyDh5oz86dQdPMhXCSwhRAFRK4j7cTERKpV\nq2Zb1mq16HQ6vL29cXNzo3///oSFheHm5kbr1q0pV66c7bm7du2iUaNGuLu7234WGRnJjRs3qFOn\nDsOGDUOhUORxS0I8njS9jiOj36L9xpO4meF4s+oUX7SJoKBi9i5NCCHu8dgfRLNarbbHer2eZcuW\nsWPHDry9vXn//fc5e/YslStXBuCbb75h4sSJtud/9NFHNG7cGF9fX/r378/OnTt59dVXH/ha/v6e\nqNWqxy0xzwUGOvd1zMLc369bF+PXbyjhN3LQ+bqQsXA2tbp+9Ayre3rOfvzA+XuU/hzfs+ox19AO\nCgoiMTHRtpyQkEBgYCAAsbGxlCpVCq327idp69aty+nTp6lcuTIGg4Hbt28THBxs27Zdu3a2x02a\nNOH8+fMPDe2UFMPjd5THAgM16HTp9i4j3xSm/vTZ6ZxOOs1p3UnO3D5Gw7V76LVLh4sFjrSsSclF\nm/HSFnGo34ezHz9w/h6lP8eX1z0+7A1ArqEdGhrKokWLCA8P58yZMwQFBeHt7Q1AyZIliY2NxWg0\n4u7uzunTp2natCkAZ8+epXz58rb9pKenM3jwYJYuXYqrqyuHDx/mlVdeedrehHigc8ln+eL8XqKv\nxPB74ikupcZixUrdG7BqCzyfAPFaN25Pn0aZdj3tXa4QQuQq19CuXbs21apVIzw8HIVCQWRkJJs2\nbUKj0dCyZUt69OhB165dUalU1KpVi7p16wKg0+lsI3AAjUZDkyZNeOedd3Bzc6Nq1aoPHWUL8TR+\nub6PLts6YjQbAfBx9aVZUCgjfjTQcstxlBYrhq4foIqcRAmNj52rFUKIR6Ow/vUidQFTEE6pOPup\nHWfs77cbv9JpWwfMFjOLX19MLb/6lD97G5/B/VFfvIC5dFnS5y0ip3FTe5f61Jzx+P2ds/co/Tm+\nAnV6XAhHcvDmATpv64jJYmL1q+voVPl1DEOH47HiMwAMvfqQEREJcq8AIYQDktAWTuPQrRje3daB\nbEsWK1/5ktdveEF4DTwvXcIUUoH0eUsw1W9g7zKFEOKJSWgLp3As/gjh37+F0ZTJqtClvL10Nx6r\nV4JSiWHAYDKGjwYPD3uXKYQQT0VCWzi8kwnH6fhdewymDL73GUqrbpNQXb+GqXIV1GtWk1Guir1L\nFEKIPCGhLRza77qTvP1dW1R37nD691CqbJuNVaUiY+hwDENGEBhcBJz8QzBCiMJDQls4rDOJp3n7\nu7Y0OpXKVz/64p24n5zqNdAvWILp+Zr2Lk8IIfKchLZwSAdu7OfjTZ1Z8G0KXX4Hq4uBjNHjMAwY\nDC4u9i5PCCHyhYS2cCgWq4WFx+ZyfvUk9n9vpWgG5NSqTfqCpZgry7VrIYRzk9AWDiPZmMSYb97n\nnRW/MOUPMLu5oh8/jsw+/UEt/ysLIZyf/KUTDuHIrRi2zXiHzzYnUyQTDHXrYFy0HHNIRXuXJoQQ\nz4zS3gUI8TBWq5V1e6Zh6tiKxeuT8bG4cGfydDK+3yOBLYQodGSkLQqsO8ZUvvvkTbp9eQK/LEio\nWwPVp19iKVvO3qUJIYRdSGiLAunaH7+Q/mEHBp8zkuGu4saUSFx7fIRFKSeHhBCFl4S2KFgsFlSr\nl1MpchReWRb+rFUW7YqtuJYua+/KhBDC7mTYIgoM5ZXL+HZ4E+2oEeRgYWW/xhTZcRKlBLYQQgAS\n2qIgsFjwWP4p2pcb4Lr/F7Y+B2+OCSFszH9AobB3dUIIUWDI6XFhV6qLF9AM7o/LoYOY/P3p11bF\nmspGdnb4Ek8XT3uXJ4QQBYqEtrAPkwmPz5bgNXMKCqMR45vt6PRyIpvv7Gdyw+lUK1Ld3hUKIUSB\nI6EtnjnV2T/RDO6Hy7GjWIoEcmfJChaWvsbm3yJoUbolvWr0tXeJQghRIMk1bfHs5OTgOXcm/i0a\n4XLsKMZ/dSR5/yGONijH5OgJFPEIZEHzpSjkOrYQQtyXjLTFM6H+/STeg/rjcvoU5mLF0c+eT3ar\n1zDkGOjzn+5kW7JZ1HwpQZ5B9i5VCCEKLAltkb+ysvCcNxPPhfNQmExkdu5KxoTJWH39ABj/WwQX\nUs/Tu0ZfWpRpZedihRCiYJPQFvlGfewImsH9UZ/9E3NwKdLnLCSnWQvb+m2XvuPff6yiakB1xtaf\naMdKhRDCMUhoi7yXmUnmxKEEr16P0mLl0tuvc2Hoh7j4aHFNPouryhVDjoGhewfgrnJnWctVuKvd\n7V21EEIUeBLaIk+pYw5i6duJ0tcTifWHHm/Cz+W2w87t933+jCZzqaSt/IyrFEIIxyShLfJGRgZe\nUybgvnIZWGFZI08Shg8l1FVJXXMW2eZsssxGsszZZJuzyDJn8XyRmnSr1sPelQshhMOQ0BZPzWX/\nL3gP7o/6ahxnA2Bcl5KMHPgDZXzK2rs0IYRwKhLa4okp0u/g9UkkHmtWYlbA9FDY+k4dVrXdSIBH\ngL3LE0IIp/NIoT116lROnjyJQqEgIiKCGjVq2NatW7eOrVu3olQqqV69OmPGjGHTpk0sWLCA0qVL\nA9CwYUP69u3L2bNnmTBhAgCVKlVi4kT5xLCjcvlpN5phH6G6cZ0Lxd3p1MaItuGrfNVqtdwzXAgh\n8kmuoX3o0CHi4uKIiooiNjaWiIgIoqKiANDr9axcuZJdu3ahVqvp3r07J06cAOD1119n5MiR9+xr\nypQpttAfNmwYP//8M02bNs2HtkR+UaSl4jU+Ao+v1mJRq5jf0peRL6XxTo1uzGgyF7VSTt4IIUR+\nyfU2ptHR0YSFhQEQEhJCWloaer0eABcXF1xcXDAYDJhMJjIzM/H19b3vfrKzs7lx44ZtlN6sWTOi\no6Pzqg/xDLju/AH/RvXw+GotaZUr0KyfF0NC0xjcIILZTRdIYAshRD7L9a9sYmIi1apVsy1rtVp0\nOh3e3t64ubnRv39/wsLCcHNzo3Xr1pQrV47jx49z6NAhevTogclkYuTIkQQEBODj42PbT0BAADqd\n7qGv7e/viVqteor28kZgoMbeJeSrXPtLTIRBg2D9eiwuajZ2rs0Hz53BQA4r2qygZ+2ez6bQJ1To\nj58TcPYepT/H96x6fOyhkdVqtT3W6/UsW7aMHTt24O3tzfvvv8/Zs2epWbMmWq2Wl19+mePHjzNy\n5Eg+//zzB+7nQVJSDI9bXp4LDNSg06Xbu4x8k1t/6i2b8Bg5CPfkNI6WUtH1DRN/BB2jhGdJPms6\nl1alXivQv5/CfvycgbP3KP05vrzu8WFvAHIN7aCgIBITE23LCQkJBAYGAhAbG0upUqXQarUA1K1b\nl9OnT9OhQwdCQkIAqFWrFsnJyfj7+5OammrbT3x8PEFBMjlEQWSxWjhxejsBYyKoe/AKmWr4uCWs\naxFA64rtmF7hX9Qr9hJKhUwSJ4QQz1Kuf3VDQ0PZuXMnAGfOnCEoKAhvb28ASpYsSWxsLEajEYDT\np09TtmxZVqxYwffffw/A+fPn0Wq1uLq6Ur58eY4cOQLArl27aNy4cb40JZ6cPusOq8Y2pm6bTtQ9\neIXosmomzOlAo5nbON7tHNMaz6Z+8QYS2EIIYQe5jrRr165NtWrVCA8PR6FQEBkZyaZNm9BoNLRs\n2ZIePXrQtWtXVCoVtWrVom7dugQHBzN8+HA2bNiAyWRiypQpAERERDB+/HgsFgs1a9akYcOG+d6g\neHS6i8eJ792G0afTyXRVcnx4d8oOmc7Hald7lyaEEAJQWB/l4rKdFITrIM5+PSYwUIMu4Q5Jy2dQ\nfMo0fI1WzlQvTuDKbSjKVbB3eU+tUBw/J+4PnL9H6c/xFahr2sLJxcVhCm9H5YMnuOMKWwe9Sf3R\n/0ahlNPfQghR0Mhf5sLKYsH9i8/JrlqJ4gdPsKOiku1Rc2kwZq0EthBCFFAy0i6ElJcvoRkyANcD\n+0lxhyFve/H6mM20KFHf3qUJIYR4CAntwsRsxuPzz/Cc8glKYybfVoJZXcoxN3wT5X1D7F2dEEKI\nXEhoFxKqC+fRDO6Py+EYUrzV9P0XXA57ie1dt2HJkE+HCyGEI5CLl87OZMJj4Tz8m4ficjiGzTVc\nea6viZy33mZj2+8I8JQpNIUQwlHISPv/2rv3uKjrfI/jr7kxXGZERgGvrMqmeDkaHmrzhmFgeVnT\n2rXcFFE8boq3yiTxgnU2TUU3yWtIm6t4WdHd46NMjNBqk/CyXhY8ZrKnIMsLeIEREGb4nj9YZ3VV\nFEqGgc/zL2fG34/v25+/33t+39+PmQZM978nMU+fhOHYUYqaehE1/DofdoU3+i5jXNcJaDQaZw9R\nCCFEDUhpN0QVFXgmLsdz+RI0FRXsecyf34Sex+z/Mz54cgMP+/V09giFEELUgpR2A6P/+3HM0yaj\nz/k7pX7NmDDEzuafneep9kNIDFtNU3cfZw9RCCFELUlpNxTXr+O5fDGeib9HY7dz+MlgInoeo9hd\ny4JebzKpxxSZDhdCCBcnpd0A6I8cwjwjBv1Xpyhv3Zp5z7dgifkILb1asXHg+/yipfz+tRBCNARS\n2q6stBSvxW/isXYlmspKjo/oz5AexzjLEcLaPsGq8CSaezR39iiFEEL8RKS0XZT+y0zMMyaj/0cu\nZQFtiX2uGYlen2IymFnS6/dEdh0nX58phBANjJS2q7Fa8Vr4Oh7J7wJw8Nl+DO56hEJtPk8ERJDQ\nfwWtzW2cPEghhBAPgpS2CzF8/inml6aiy/uGkg7tmPorL97z/Bwfow+r+r7Nrzo+JzebCSFEAyal\n7QI0xUV4LZiHx8Y/oA0LWzIAABGpSURBVLRaPvt1H37Z+RBF2nKGBY5gYb+l+Hn6OXuYQgghHjAp\n7XrOkPEx5penofv+LD+082PsL2183OwL/Dz9WRG6nCEdfunsIQohhKgjUtr1lObKZUzz43DfmoJN\np+HNMD2v97mAu2cTJneZxoyer8gHpQghRCMjpV0PGT76EOMrMbgXXOJvLWDccMWVjm2I/48X+U3n\nMZjczM4eohBCCCeQ0q5HNIWFFE9/gfZ7D3BdB7OfgE+feZQZPacxqP0QdFqds4cohBDCiaS06wOl\nUDs34xY7g/ZF18lqA5umhjNk8Gxe9n/E2aMTQghRT0hpO5nm/HlsM8bR4pO/UqqHpSNa0et3O5jv\n29XZQxNCCFHPSGk7i1IY/rQZt9kv4Wkt47MA+HR2FOOHJ+Cmc3P26IQQQtRDUtpOoP3+LNoZE2m6\n/3OsBpg7vCmPzNvEi21DnT00IYQQ9ZiUdl1SCuOmDRjnz8J4rYz09rBj2mBe+dVavI1NnT06IYQQ\n9ZyUdh25/NXfcJ/xIr5HTlHkBq+O8KDLy4m80ek5Zw9NCCGEi5DSfkAqVSUnLh4j/f/20HTjJqb+\n+TtMFbD757B+wqPM/fV7tDUHOHuYQgghXMh9lfbChQs5fvw4Go2GuLg4unfv7ngtJSWFXbt2odVq\n6datG3PmzMFmszFnzhzy8vKw2+3MmjWLkJAQxowZQ0lJCZ6engDExsbSrVu3B5PMCYquX+XT7/aT\n/m0an+R9jDn/PMm7oP+3UOyp588zhuMfHctan47yxR5CCCFq7J6lffDgQb799lu2bdtGbm4ucXFx\nbNu2DQCr1UpycjJ79+5Fr9czfvx4jh07Rm5uLh4eHmzZsoWvv/6a2bNnk5qaCsCiRYvo2LHjg01V\nR26cTWfkpbMv/xMOnzuIXdnRVkLcES/mfqzDWG7H+uSTlCe8Q1//Fs4eshBCCBd2z9LOzMwkPDwc\ngMDAQK5evYrVasVkMmEwGDAYDI6z59LSUry9vRk2bBhDhw4FwGKxcOXKlQebog6dLznP/rxP2Jf/\nCZ/mZ1BYVgiAVqMl2K8nI+nBxDWZND1xkspmzShalMD1p58BObMWQgjxI92ztAsKCuja9V8f9GGx\nWLh48SImkwmj0UhMTAzh4eEYjUaGDBlC+/btb1l+w4YNjgIHSExM5PLlywQGBhIXF4e7u/tPGOfB\nsVXamPvXWN7LTnI818KrJaOCRjMgIJzQFn1plbwRr6WL0JSXUzb8GawLE1DNmztx1EIIIRqSGt+I\nppRy/NlqtbJu3Tr27NmDyWRi7NixnDp1iqCgIKDqendOTg5r164FIDIykk6dOhEQEEB8fDwpKSlE\nR0ff9Wf5+Hii1zv/87bdm8BzqS/w0ZmP6Ny8M+ODx/PUz5+iq2/XqmvTJ07Ar5+DI0fA3x/WrMF9\nxAhc4+0I+Po27C8gkXyur6FnlHyur64y3rO0/fz8KCgocDy+cOECvr6+AOTm5tK2bVssFgsAISEh\nZGdnExQUxPbt28nIyGD16tUYDAYAIiIiHOsZMGAAu3fvrvZnX75cUvNEP7FyYxFPbRxMdsEJwto+\nwfonN2B2awJAwfeX8FyxDM+3E9BUVFD23G+wvrEQ5WOBi8VOHvn98fU1c9FFxlobks/1NfSMks/1\n/dQZq3sDoL3Xwn369CEtLQ2AnJwc/Pz8MJlMALRu3Zrc3FzKysoAyM7Opl27duTn57N161ZWrlyJ\n0WgEqs7Qo6KiKCoqAiArK4uHHnroxyV7wLIL/s4v1v+C7IITjOkyjk2D/+QobP3xo/gMfByvpYuo\n9PXj6ubtFL+ztqqwhRBCiAfgnmfaPXv2pGvXrjz//PNoNBri4+PZuXMnZrOZiIgIoqOjiYyMRKfT\nERwcTEhICMuXL+fKlStMnDjRsZ7k5GRGjhxJVFQUHh4e+Pv7M3Xq1Aca7sfIyEsnOi2SaxVW5vV6\ngykPT6+aCi8rw2vZYjxWvo3Gbqd0TBTX4v8b1cTb2UMWQgjRwGnUzRep6xlnTan8MecPxH72Mnqt\nnj+O+CNhfoMA0B8+iHlGDPrTX2EP+BnFyxKp6B/mlDH+VBr61JXkc30NPaPkc331anq8MalUlfwu\ncwEzP52Ot9GbHcM+YGTXkVBSglf8HJoOHYj+9FeUTPgtl/ZnunxhCyGEcC3yMab/dOhcFssOLyYj\nL50O3oFsHppKB+9A+OwzfKLGof+/f2Br3wHritVUPNbb2cMVQgjRCDXq0q5UlaR98xGrjq7g4Lkv\nAejXuj9JT76PxWbENHsmJL+LTqulZNJUrsXOgX9+BKsQQghR1xplaZfZykg9vY3VxxI5c+VrAMID\nBhITPJ3erfri9tl+zK9MQ5f3LXTuzJVl72ALedTJoxZCCNHYNarSvlJ2mfdzkkk6sZaLpRcwaA08\nH/QCkx+eRpClM5qiq3jNnI7HxvdROh3XZszE663fYSsqd/bQhRBCiMZT2iUVJfTZ8ggXSy9gdmtC\nzMPTmdh9Ei1NrQBw+2Qvplemo/v+LLYu3ShOXI2t+8N4GY2AlLYQQgjnazSl7aZzY/jPn6GVqQ1j\nuoylibHq96o1ly9hmjcb9z9tQRkMXHt1NiXTXwE3NyePWAghhLhVoyltvVbPm/2W3PKc2+4PMM16\nCd2F81T0CKZ4xWrsXbreZQ1CCCGEczWa0r6ZpqAA05xXcf/zDpTRiHXuAkonTwN9o/znEEII4SIa\nV0sphfF/dmKaPRNtYSEV//lI1dl1x07OHpkQQghxT42ntCsrMU+Krjq79vDA+sZCSv9rEuic/9Wf\nQgghxP1oPKVdVobb/gzK+/SjeFkilR0CnT0iIYQQokYaT2l7elKYkyvXrYUQQrisxvWFIVLYQggh\nXFjjKm0hhBDChUlpCyGEEC5CSlsIIYRwEVLaQgghhIuQ0hZCCCFchJS2EEII4SKktIUQQggXIaUt\nhBBCuAgpbSGEEMJFSGkLIYQQLkJKWwghhHARGqWUcvYghBBCCHFvcqYthBBCuAgpbSGEEMJFSGkL\nIYQQLkJKWwghhHARUtpCCCGEi5DSFkIIIVyE3tkDqGsLFy7k+PHjaDQa4uLi6N69u+O1lJQUdu3a\nhVarpVu3bsyZMwebzcacOXPIy8vDbrcza9YsQkJCGDNmDCUlJXh6egIQGxtLt27dnBXrFjXNuHPn\nTlasWEFAQAAAvXv3ZtKkSZw6dYoFCxYA0KlTJ15//XVnxLlNTfOtWbOGAwcOAFBZWUlBQQFpaWkM\nGDCAFi1aoNPpAEhISMDf398pmW5WXb709HTWrFmDm5sbQ4YMYfTo0Xdd5ocffmDWrFnY7XZ8fX1Z\nunQpbm5uzorlUJt8S5Ys4ciRI9hsNn77298ycOBAXnvtNXJycmjatCkA0dHRPP74486IdJuaZszK\nymL69Ok89NBDAHTs2JF58+Y1mG24fft2du3a5fg72dnZHD16tF4fR0+fPs3kyZOJiopy/D+84cCB\nAyxfvhydTkdoaCgxMTFAHe2HqhHJyspSEydOVEopdebMGTVy5EjHa8XFxSosLExVVFQopZQaN26c\nOnr0qEpNTVXx8fFKKaVOnz6tnn32WaWUUqNHj1ZfffVV3Qa4D7XJuGPHDvXWW2/dtq7Ro0er48eP\nK6WUevnll9X+/fvrIEH1apPvZjt37lRJSUlKKaXCwsKU1Wqto5Hfn+ry2e12FRoaqgoLC5Xdblfj\nx49XP/zww12Xee2119Tu3buVUkotW7ZMpaSk1HGa29UmX2ZmppowYYJSSqlLly6p/v37K6WUio2N\nVRkZGXWe4V5qk/HLL79UU6dOvW1dDWUb/vvyCxYsUErV3+PotWvX1OjRo9XcuXPVxo0bb3t90KBB\n6vvvv1d2u12NGjVKff3113W2Hzaq6fHMzEzCw8MBCAwM5OrVq1itVgAMBgMGg4GSkhJsNhulpaV4\ne3szbNgwZs+eDYDFYuHKlStOG//9qE3GOykvL+fs2bOOd9BhYWFkZmbWTYhq/Jh8NpuNLVu23Pau\nuT6pLt/ly5dp0qQJFosFrVbLY489xoEDB+66TFZWFk888QTgGtvvbvkeeeQRVqxYAUCTJk0oLS3F\nbrc7LcO91Cbj3TSUbXizVatWMXny5Dofd024ubmRlJSEn5/fba/l5+fj7e1Ny5Yt0Wq19O/fn8zM\nzDrbDxtVaRcUFODj4+N4bLFYuHjxIgBGo5GYmBjCw8MJCwujR48etG/fHoPBgNFoBGDDhg0MHTrU\nsXxiYiIvvPAC8+fPp6ysrG7D3EVtMgIcPHiQ6Ohoxo4dy8mTJx073w3NmjVzrMeZapsPYO/evfTt\n2xd3d3fHc/Hx8YwaNYqEhARUPfhwwOryWSwWrl27xjfffENFRQVZWVkUFBTcdZnS0lLHNJwrbL+7\n5dPpdI7p09TUVEJDQx2XNDZt2kRkZCQvvfQSly5dqvtAd1CbjABnzpzhxRdfZNSoUXzxxRcADWYb\n3nDixAlatmyJr6+v47n6eBzV6/W3HCdudvHiRSwWi+Pxjfx1tR82umvaN7v5IG21Wlm3bh179uzB\nZDIxduxYTp06RVBQEFB1rTQnJ4e1a9cCEBkZSadOnQgICCA+Pp6UlBSio6OdkqM695OxR48eWCwW\nHn/8cY4ePUpsbCzr16+/63rqk5pswx07dtxyXX7atGn069cPb29vYmJiSEtL46mnnqrzDNW5OZ9G\no+Gtt94iLi4Os9lMmzZt7rlMdc/VBzXJl56eTmpqKu+99x4ATz/9NE2bNqVz5868++67rFy5kvnz\n59fp+O/H/WRs164dU6ZMYdCgQeTn5xMZGcnevXvvup76pCbbMDU1lREjRjgeu8pxtDYe1H7YqM60\n/fz8bnnXd+HCBcc7vtzcXNq2bYvFYsHNzY2QkBCys7MB2L59OxkZGaxevRqDwQBARESE48atAQMG\ncPr06TpOc2e1yRgYGOi4gSc4OJhLly7h4+Nzy6WA8+fP33GqqK7VdhuWlJRw7ty5Ww4iw4cPp1mz\nZuj1ekJDQ+vFNqwuH8Cjjz7K5s2bWbduHWazmdatW991GU9PT8eZiytsP7hzPoDPP/+ctWvXkpSU\nhNlsBqBXr1507twZcJ19EO6c0d/fn8GDB6PRaAgICKB58+acP3++QW1DqJruDw4Odjyur8fR6vx7\n/hvbpa72w0ZV2n369CEtLQ2AnJwc/Pz8MJlMALRu3Zrc3FzHP252djbt2rUjPz+frVu3snLlSsc0\nuVKKqKgoioqKgKr/iDfu+nS22mRMSkrigw8+AKrumLxReh06dODw4cNA1dRyv379nJDoVrXJB3Dq\n1Ck6dOjgWE9xcTHR0dGUl5cDcOjQoXqxDavLBzBhwgQKCwspKSlh37599OrV667L9O7d2/G8K2w/\nuHO+4uJilixZwrp16xx3igNMnTqV/Px8wHX2Qbhzxl27dpGcnAxUTb8WFhbi7+/fYLYhVBWWl5eX\nY6q4Ph9Hq9OmTRusVivfffcdNpuNffv20adPnzrbDxvdt3wlJCRw+PBhNBoN8fHxnDx5ErPZTERE\nBFu3bmXnzp3odDqCg4OZNWsWy5cv58MPP6RVq1aOdSQnJ5Oens769evx8PDA39+fN998Ew8PDycm\n+5eaZjx37hyvvvoqSilsNpvjVxXOnDnD/PnzqayspEePHo4b8pytpvkA0tLSOHDgwC3T4xs2bOAv\nf/kLRqORLl26MG/ePDQajbNiOVSXb+/evaxatQqNRsP48eMZNmzYHZcJCgriwoULxMbGcv36dVq1\nasWiRYscM0XOVNN827Zt45133rnl/oTFixeTl5fH0qVL8fDwwNPTk0WLFtGsWTMnJvuXmma0Wq3M\nnDmToqIiKioqmDJlCv37928w2xCq3kS//fbbt1x62717d708jmZnZ7N48WLOnj2LXq/H39+fAQMG\n0KZNGyIiIjh06BAJCQkADBw40DGlXxf7YaMrbSGEEMJVNarpcSGEEMKVSWkLIYQQLkJKWwghhHAR\nUtpCCCGEi5DSFkIIIVyElLYQQgjhIqS0hRBCCBchpS2EEEK4iP8HVC0AVOgd5xYAAAAASUVORK5C\nYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ }
+ ]
+}